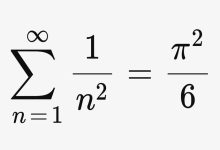İstatistikler ve olasılıklar ile ilgili bilgileri hepimiz okullarda öğrenir ve farkında çoğu zaman varmasak da günlük yaşantımızda yoğun bir biçimde kullanırız. Ancak aslında bakarsanız bu oldukça yeni bir gelişmedir. 17. yüzyıla kadar, olasılık teorisi hakkında kimsenin bir bilgisi yoktu.

Herhangi bir kimsenin gelecekteki bir olayın sonucunu herhangi bir doğruluk düzeyiyle tahmin etmesinin imkansız olduğu düşünülürdü. Kumarbazlar bile olasılıkları anlamıyorlardı. Aslına bakarsanız tam da bu nedenle olasılık teorisi yaşantımıza girdi.
Matematiğin büyük bir kısmının kökleri binlerce yıl öncesine, Öklid’e ve hatta daha önceki düşünürlere kadar uzansa da, olasılığın tarihi çok daha kısadır. Girolamo Cardano’nun ünlü 1564 tarihli el yazması
De Ludo Aleae, olasılık üzerine yazılmış en eski yazılardan biri olup, yazdıktan bir yüzyıl sonrasına kadar yayınlanmamıştır ve esas olarak zar oyunlarını analiz eder.

Galileo ve diğer 17. yüzyıl bilim insanları bu girişime katkıda bulunmuş olsalar da, birçoğu olasılığın matematiksel temellerini 1654’te iki ünlü Fransız matematikçi Blaise Pascal ve Pierre de Fermat arasındaki mektuplaşmaya bağlar. Onlar da aslında zar atışlarıyla ilgileniyorlardı.
Olasılık Teorisi Nasıl Doğdu?
17. yüzyıl Fransa’sında iki kişi ile oynanan popüler bir şans oyunu vardı. Oyuncular sırayla dört zar atıyorlar ve en az bir altı gelmesini umuyorlardı. Oyun öncesinde oyuncular eşit miktarda parayı ortaya koyuyorlar ve önceden bir kişinin ortadaki parayı alması için kaç defa kazanması gerektiği konusunda anlaşıyorlardı.

Kendisini Chevalier de Méré olarak adlandıran yazar ve amatör matematikçi Antoine Gombaud işin arka planındaki matematiği sezmişti. Bir zar atışında 6 gelme olasılığının 1/6 kadar olduğunu anladıktan sonra, iki zar atışında bunun nasıl olacağı üzerine çalışmaya başladı.
Sonrasında bir zarda (6,6) gelme olasılığının 1/36 olduğunu ortaya attı. ( Doğru buldu!). Ancak yanıldığı bir yer vardı. Bir çift zarı 6 kez atmanın bunun için yeterli olduğunu düşündü. Bu nedenle De Méré sürekli olarak bahsi kaybetti.
Sonunda 1654’te de Méré, arkadaşı Pascal’a akıl danışmaya karar verdi. Örneğin, iki adil zarın 24 atışında bir çift altı geleceğine para yatırmanın akıllıca olup olmadığı gibi soruların cevabını merak ediyordu. Pascal bir süre uğraştıktan sonra konuyu daha yaşlı bir meslektaşı olan Pierre de Fermat’a bir mektup ile iletti. İkisi, birkaç hafta süren bir yazışmada problemi ileri geri tartıştılar. Mektupların çoğu daha sonra yayınlandı ve olasılık teorisinin temel belgeleri haline geldiler.
Olasılık Matematiksel Altyapısını Çok Daha Sonra Kazandı
Bu yazışmalar Abraham de Moivre, Christiaan Huygens, Siméon Poisson, Jacob Bernoulli, Pierre-Simon Laplace ve Karl Friedrich Gauss’un 19. yüzyıla kadar önemli ilerlemeler kaydetmesine ilham verdi. Yine de uzun bir süre boyunca, matematikte kesin bir olasılık tanımı yoktu. Cardano’dan yaklaşık dört yüzyıl sonra, 1933’te Rus matematikçi Andrey Kolmogorov, olasılık teorisini aksiyomatik bir temele oturtana kadar da olmadı.

Olasılık teorisinin bir alt alanı olan optimal durdurma problemlerinin tarihi de kumarla başlar. En erken keşiflerden biri Cambridge Üniversitesi’nden seçkin İngiliz matematikçi Arthur Cayley’e atfedilir. Kendisi 1875’te piyango bileti satın almak için optimal bir durdurma stratejisi bulmuştu.
İlerleyen yıllarda olasılık teorisi şans oyunlarının dışına taşınmaya başlanacaktı. II. Dünya Savaşı sırasında Abraham Wald ve diğer matematikçiler, askeri ve endüstriyel karar vericilere yardımcı olmak için istatistiksel analiz alanını geliştirdiler.
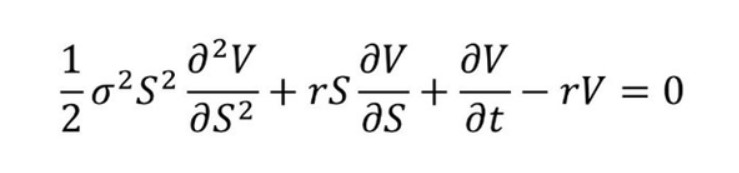
1970’lerde de, Fischer Black ve Myron Scholes hisse senedi opsiyonlarını değerlendirmek için öncü bir formül keşfettiklerinde optimal durdurma teorisi finans alanında önemli bir araç olarak ortaya çıktı.
Sonuç olarak
Bir kumar probleminin çözümü, şans oyunları, sigortacılık, iş planlaması, tıp gibi alanların çok ötesine geçti. Pascal ve Fermat hiçbir zaman yüz yüze tanışmadılar. Ancak onların işbirliği gelecekle ilgili tüm dallara damgasını vurdu.
Kaynaklar ve İleri Okumalar:
- Porter, Theodore M.. “probability and statistics”. Encyclopedia Britannica, 6 Mar. 2024, https://www.britannica.com/science/probability. Accessed 11 August 2024.
- July 1654: Pascal’s Letters to Fermat on the “Problem of Points”Yayınlanma tarihi: 1 Temmuz 2019. Bağlantı: July 1654: Pascal’s Letters to Fermat on the “Problem of Points”
- An Epistolary Episode. Kaynak site: American Sceintist – Mayıs 2009. Bağlantı: An Epistolary Episode
- Debnath, Lokenath & Basu, Kanadpriya. (2015). A short history of probability theory and its applications. International Journal of Mathematical Education in Science and Technology. 46. 10.1080/0020739X.2014.936975.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel