Matematikçilere dair anlatılan hikayeler arasında, en duygu dolu ve etkileyici olanlardan biri de Galois’nın hikayesidir. Bu dahi çocuk, çok genç yaşlarda çığır açan buluşlar yapmış ancak 21 yaşında bir düelloda hayatını kaybetmiştir.
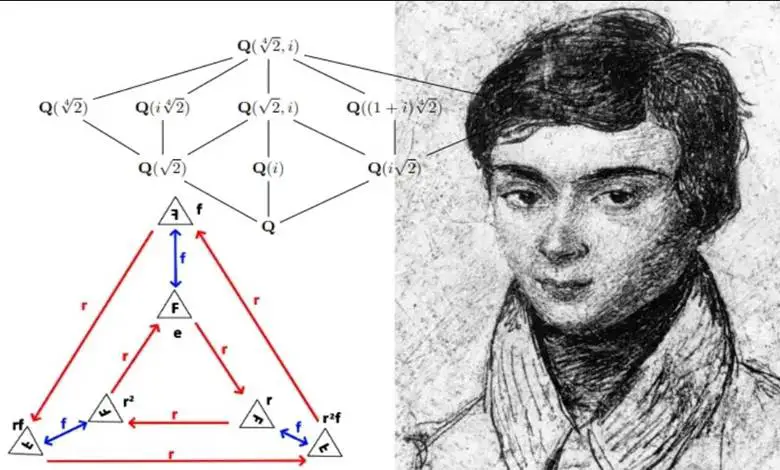
Eğer onun hikayesini okumadıysanız bu yazımıza göz atmalısınız. Eğer okuduysanız aklınızda ölümünden önceki son gece üzerinde çalıştığı iddia edilen “Galois teorisi nedir?” sorusu kalacaktır. Bu yazıda mümkün oldukça soyut matematiğe girmeden bu konuyu anlamaya çalışalım.
Muhtemelen hepiniz 2. dereceden denklemleri yani ax²+bx+c = 0 biçimindeki denklemleri çözmenin yöntemlerini biliyorsunuzdur. Bunun için genellikle aşağıda gördüğünüz denklemi kullanırız. Farkındaysanız bu formülde karekök yer almaktadır.
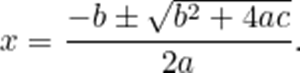
Aslına bakarsanız, katsayıları a, b, c ve d olan olan üçüncü dereceden bir denklem için de benzer ama daha karmaşık bir formül vardır. Polinom (çokterimli) denklemlerin radikallerinin (karekök, küp kök, vb) değerlerini bulma işlemi, denklemin derecesi büyüdükçe hızla karmaşıklaşır.
İkinci dereceden denklemlerin çözümü için kullanılan genel formül, dokuzuncu yüzyıl civarında biliniyordu. Üçüncü ve dördüncü dereceden denklemlerin çözümü için kullanılan formüller ise on altıncı yüzyılın ilk yarısında keşfedildi. Doğal olarak sıradaki hedef, beşinci dereceden denklemlerdi. Galois’ dan önce, 300 yıl boyunca birçok matematikçi umutsuz bir biçimde çözümü verecek formülleri bulmaya çalıştı ama bir işe yaramadı. Peki 5 sayısını özel şey yapan şey nedir?
Evariste Galois’in Ölümünden Önceki Son Gece Çalıştığı Konu Neydi?
Aslında bu soru 1800’lerin başında Galois’i de rahatsız ediyordu. Nihayetinde bir düelloda ölümcül şekilde yaralanmadan önceki gece, sorunu şaşırtıcı derecede zarif bir şekilde çözen yeni bir matematiksel teori ortaya çıkaracaktı.

Matematikçiler simetrileri incelerken grup teorisini kullanırlar. Grup teorisi modern matematiğin temelini oluşturur ve diğer alanlarla da büyük ölçüde ilgilidir. Ve evet. Doğru tahmin ettiniz. Grup teorisinin Evariste Galois ile ilgisi vardır.
Aslında gruplar ilk kez dolaylı olarak 1770 civarında Lagrange tarafından tanıtılmıştı. Joseph-Louis Lagrange, ikinci dereceden denklemleri çözmek için okulda öğrendiğiniz tanıdık formül gibi, belirli denklem türlerinin çözümlerini size verecek formüller bulmak istemişti. Devamında da beş ve daha yüksek dereceden denklemlerin çözümü için simetrilerin kullanılabileceğini düşünmeye başlayacaktı.
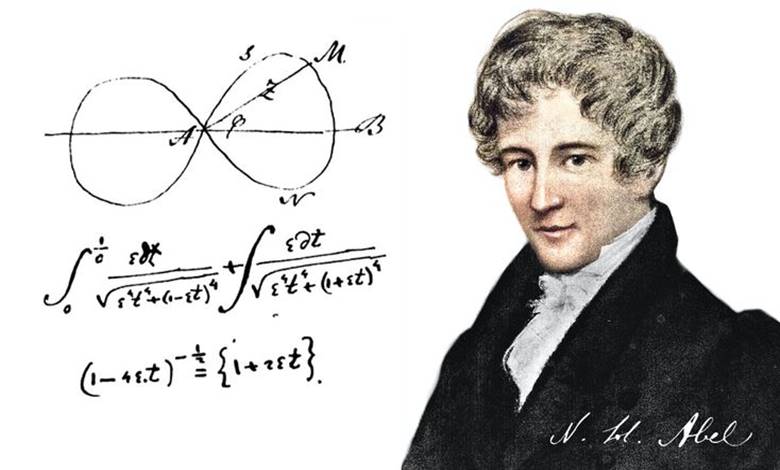
İlerleyen süreçte 1824’te Nils Henrik Abel adındaki bir başka genç de benzer konulara kafa yormaya başladı. Ancak ne yazık ki tüberkülozdan 26 yaşında yaşamını yitirecekti. Ancak Abel tarafından ispatlanan sonuç beşinci dereceden bir denklemin genelleştirilmiş bir çözümünün olamayacağı biçimindeydi.
Simetrinin cebirdeki rolü şaşırtıcı görünebilir. Çünkü çoğumuz simetriyi fiziksel nesneler veya geometrik şekiller üzerindeki yansımalar, döndürmeler ve benzeri diğer işlemler açısından düşünmeye alışkınız. Ancak bu çok farklı nesnelerin simetrileri temelde aynıdır. Sonunda, 1830’larda Évariste Galois, Lagrange’in ve Abel’in çalışmalarını temel aldı. Sonucunda da onu ölümsüzleştiren Galois teorisi ortaya çıkacaktı.
Galois Teorisi Nedir?
Évariste Galois, Beşinci (veya daha yüksek) dereceden bir polinom denkleminin kökleri için, polinomun katsayıları açısından, yalnızca olağan cebirsel işlemleri ve kökleri kullanarak neden bir çözüm bulunamayacağına kafa yormaya başlamıştı. Sonrasında da Galois teorisi ile soyut cebirin iki alt alanını birbirine bağladı. Bu iki alan grup teorisi ve cisimler idi.
Grup Teorisi Nedir?
Grup teorisi simetrileri ele alır. Bunun en bilinen örneği karedir. Bir kareye simetrik diyoruz çünkü onu 90 derecenin katları arasında döndürebilirsiniz. Sonuç yine bir kare olacaktır. Bir matematikçi kare masanın simetrilerinden oluşan kümenin 90, 180, 270 ve 360 derecelik açılara karşılık gelen dört eleman içerdiğini söyleyecektir.
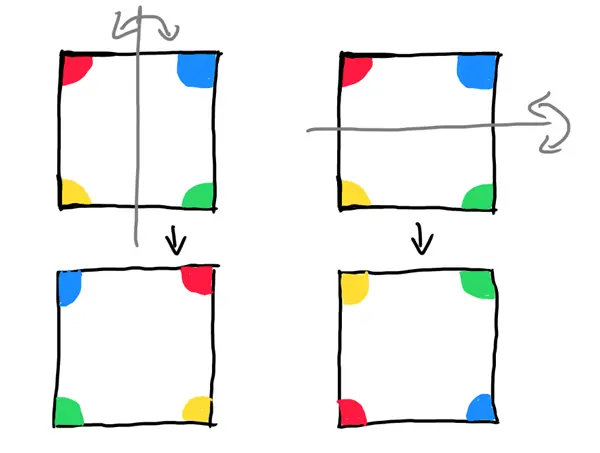
Bu dönme hareketlerinden ikisini arka arkaya uyguladığımızda, bir başka dönme hareketini elde ederiz. Sonucunda 450 derecelik dönme hareketi, 90 derecelik dönme hareketinin aynısıdır, çünkü 450=360+90’dır. Aynı biçimde 270 derecelik dönme hareketinin 90 derecelik dönme hareketinin tersi olduğunu da biliyoruz. Ayrıca istersek etki etmeyecek 0°’lik döndürme hareketi de yapabiliriz.
Bu üç yapıya sahip dönme hareketlerinin kümesi, matematikçilerin grup ismini verdikleri kavrama bir örnek teşkil etmektedir. Elimizde bir G kümesi ve bir de * işlemi olsun. Bu durumda bir grup aşağıdaki özellikleri sağlamalıdır.
- Grubun g, h gibi iki elemanı üzerinde verilen işlemi yaparsanız, grubun başka bir elemanını elde edersiniz.
- Grubun bir etkisiz elemanı ( e) vardır. Sonucunda g*e = e*g = g olmalıdır.
- Grubun içinde her g elemanı için ters bir a elemanı vardır öyle ki g*a = a*g = e olmalıdır.
Aslına bakarsanız temel düzeyde matematik eğitimi alan herkes yukarıda yazdığımız özelliklere aşinadır. Sonucunda tamsayılarda toplama ya da çarpma işlemini öğrenirken de bu bilgiler verilmiştir. Yani temelinde tamsayılar kümesinde toplama veya çarpma işlemi de bir gruptur.
Ancak grupların simetri ile ilgili olduğunu ve örneğin toplama işleminde bir simetri olmadığını düşünebilirsiniz. Aslına bakarsanız toplama işleminin öteleme simetrisi mevcuttur. Sonucunda bir tam sayıyı başka bir sayı ile toplamak, verilen sayıyı belli bir adım kadar sayı doğrusu üzerinde sağa ya da sola doğru ötelemek anlamına gelir.
Cisim ( Number Fields) Nedir?
Cisim, soyut bir cebirsel yapıdır. Kabaca, elemanları arasında toplama, çıkarma, çarpma ve bölme (sıfıra bölme hariç) yapılabilen ve bu işlemlerde sayılardan alışık olduğumuz temel aritmetik kurallarının geçerli olduğu bir küme olarak tanımlanabilir.
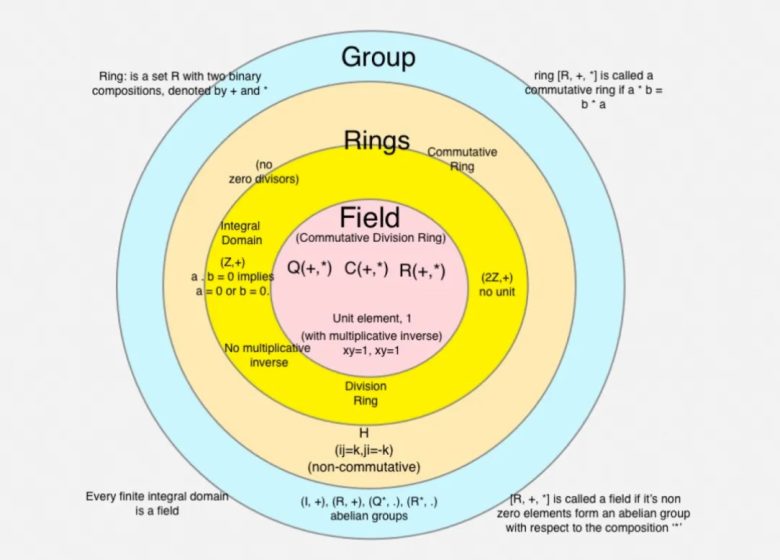
İkinci dereceden denklemleri düşündüğümüzde bir miktar simetri algılayabiliriz. Örnek olarak, ikinci dereceden x2-2=0 denkleminin x1=√2 ve x2=-√2 biçiminde iki tane cevabı vardır. Bu iki cevap temsil ettikleri sayılar açısından farklı olsalar da temelinde simetriktir. Yani x1 ve x2 nin yerlerini değiştirmek sonucu değiştirmeyecektir.
Şimdi bir miktar genelleme yapmamız gerekiyor. Bunun için yeni bir sayı kümesi tanıtalım. Bu sayı kümemiz Q(√2) biçiminde olsun. Burada Q rasyonel sayıları temsil ediyor. Bu kümemizin içine a+b√2 biçiminde yazılabilen bütün sayıları dahil ettiğimizi düşünelim. ( a ve b rasyonel sayı olmak zorunda).
Yeni oluşturduğumuz bu sayı kümesini şimdi biraz inceleyelim. Sonucunda b=0 kabul edersek geriye kalan a tüm rasyonel sayıları temsil ediyor. Ayrıca a=0 ve b=1 kabul edersek √2 ve b=-1 kabul edersek -√2 sonuçlarına ulaşıyoruz. Sonucunda Q(√2)’yi tüm rasyonel sayıları içeren en küçük cisim olarak düşünebilirsiniz.
Bir polinom verildiğinde, kökler çeşitli cebirsel denklemlerle bağlanır. Galois’nın teorisinin ana fikri, köklerin permütasyonlarını dikkate almaktır. Böylece kökler tarafından sağlanan herhangi bir cebirsel denklem, kökler değiştirildikten sonra hala geçerliliğini korur. Bu permütasyonlar Galois grubu adı verilen bir grup oluşturur.
Galois Teorisi İle İlgili Bazı Örnekler
Aslında Galois, radikallerin (karekök, küpkök, vb) çözümleri için bir formülün ancak ve ancak karşılık geldiği Galois grubunun basit yapıda olması koşuluyla var olabileceğini göstermeyi başarmıştır. Günümüzde matematikçiler bu tür bir gruba çözülebilir grup derler.
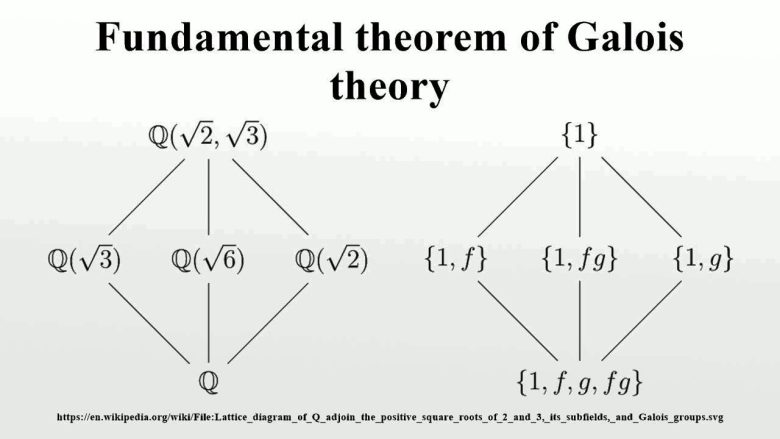
İkinci, üçüncü ve dördüncü dereceden denklemler için Galois grupları her zaman çözülebilir niteliktedir. Ancak Galois, beşinci dereceden (ya da daha üst dereceden) tipik bir denklemin simetri gruplarının çözümsüz olduğunu göstermiştir. Yani temelinde matematikçilerin onlarca yıllık çabası nafiledir.
x2-2=0 denklemi için Galois grubunu yukarıda tanımladık. Bu denklemin rasyonel sayılara eklediğimiz iki çözümü vardı. Bu durumda ortaya çıkan sayı cisminin Galois grubu iki eleman içerir. Şimdi üçüncü dereceden denklemi ele alalım. Katsayılarının rasyonel sayılar olup, üç çözümünün de irrasyonel sayı olduğunu varsayalım.
Bu çözümleri rasyonel sayılara ekleyerek yeni bir sayı cismi oluşturabiliriz. Bunu bir bardak çaya üç farklı katkı maddesi eklemeye benzetebiliriz. Bu sayı cisminin (katkıların karıştırıldığı çay bardağı) herhangi bir simetrisinde, üçüncü dereceden denklem değişmeyecektir. Çünkü katsayıları simetri tarafından sabit korunan rasyonel sayılardır.
Bu yüzden, üçüncü dereceden denklemin her bir çözümü (üç katkı maddesinden biri) kaçınılmaz olarak başka bir çözüme gidecektir. Bu gözlem sayesinde, bu sayı cisminin simetrilerinin Galois gruplarını bu üç çözümün permütasyonları cinsinden tanımlamak mümkündür. Üstelik bu çözümler için herhangi bir formüle ihtiyacımız yoktur. Bu şekilde, çözümlerini katsayılar cinsinden ifade etmeden denkleme dair birçok çıkarımda bulunabiliriz.
Galois’nın çalışması, matematiksel iç görünün gücüne dair harika bir örnektir. Galois, polinom denklemlerin çözümü için bir formül bulma problemini bilindik biçimde çözmedi. Problemi yeniden formüle etti ve ona tamamen farklı bir açıdan baktı.
Kaynaklar ve ileri okumalar
- Galois theory for non-mathematicians. Yayınlanma tarihi: 26 Aralık 2019; Bağlantı: https://towardsdatascience.com/
- For the Love of Mathematics. yayınlanma tarihi: 9 Şubat 2022; Bağlantı: https://www.cantorsparadise.com/
Matematiksel





