
Sayıları kullanmaya başladığı ilk günden itibaren insan sayıların içinde saklı sırlar arar durur. Bulduğu sırları da tanrıların kendisine yaptığı oyunlar olarak değerlendirir. İşte binlerce yıl insanları meşgul eden “sihirli kareler” de bu sırlardan biri ile ilgilidir.
Sihirli kareler karşımıza ilk olarak MÖ 650 yılında kaleme alınan Lo Shu efsanesinde karşımıza çıkar. Anlatıya göre Eski Çin’de büyük bir sel olur. Bunu için de halk arasında lânetli olduğuna inanılan Sarı Irmak’ın kenarlarına topraktan bir set yapılmasına karar verir. Çalışmaları kontrol etmek içine gelen bilge imparator bir kaplumbağa görür. Kaplumbağanın kabuğunda İmparatorun o güne kadar hiç görmediği bir şekil vardır.

Bilge imparator, bu şekli hemen Lo shu adıyla kayıt altına aldırır. Görseldeki 3’lü sihirli kareye Lo shu karesi denir. Bu kareye sihirli kare denmesinin nedeni, sayıların belirli bir düzene göre dizilmesidir. Lo shu karesinin tüm satır ve sütunları ile köşegenlerinde bulunan sayıların toplamı hep aynı sayıya yani 15’e eşittir. On beş aynı zamanda Çin güneş yılının 24 döngüsünün her birindeki gün sayısıdır.
Sihirli Kareler Tarih Boyunca Bir Çok Matematikçinin İlgisini Çekmiştir.
Sihirli karelerin Çin’de başlayan serüveni İpek Yolu kervanlarıyla Hindistan’a taşınacaktı. Batıda konuyla ilgili ilk yazılı kaynak yaklaşık olarak M.S. 130 yılına ait İzmirli Theon’un yapıtıdır. 9. yy’da ise Arap dünyasına giren sihirli kareler Arap astrologlar tarafından gök haritalarının çiziminde kullanılacaktı.
Sihirli kareler Alman sanatçısı Albrecth Dürer’in (1471-1528)’in kabartma resminde görülmektedir. Dürer 1514 yılında bakır plaket kabartma üzerine sağ üst köşesine sihirli kareyi yerleştirerek Melencolia’ı (Melancholia 1) yapmıştır. Bir ressam olan Albrecth Dürer matematik ve sanat arasındaki ilişkiyi incelemiştir. Detaylar için: Albrecht Dürer Melencolia1 İle Bize Ne Anlatmak İstiyor?

Bir ara Ortaçağ Avrupası’nda da moda olan sihirli kareler, henüz bilimsel düşüncenin egemen olamadığı zamanın Avrupa’sında pek çok başka bilimsel düşüncede ve olayda olduğu gibi dinsel ya da matematiksel olgularla ilişkilendirilmiştir. Günümüzde sihirli karelerin kutsal bir özelliği olmadığını hepimiz biliyoruz. Ancak yine de matematikçiler açısından bu karelerin ilginç bir çok özelliği bulunmaktadır.
Sihirli Kareler Nedir?
Sihirli kare, içinde 1’den n’e kadar sayıların yazılı olduğu nxn boyutlarında bir karedir. Ancak bu sayılar öyle yazılmışlardır ki her satır, sütun ve köşegenin toplamı aynı sayıya eşittir.
Bu kareler, 1’den n2 ’ye kadar olan farklı tam sayıların kare şeklinde dizilmesiyle oluşur. Öyle ki karenin tüm satır, sütun ve köşegenlerinde bulunan sayıların toplamı birbirine eşittir. Bu karede bulunan tam sayıların toplamı 1+2+3+…(n-1)+n+(n+1)+…+n2 =(n2 (n2 +1))/2 ’dir.
Bu karede toplamda n tane satır veya sütun olduğu için her bir satırdaki veya sütundaki sayıların toplamı (n2 (n2 +1))/2n formülüyle bulunur. Örneğin 5’li sihirli karedeki tüm sayıların toplamı 325’e eşittir. Ayrıca bu karenin her bir satır, sütun ve köşegeninde bulunan sayıların toplamı 65 olur.
5×5’lik Bir Sihirli Kare Yapalım
Sihirli kare yapmak için pek çok yöntem mevcuttur. Şimdi bunlardan biri ile 5×5 boyutunda birini yapmaya başlayalım. Öncelikle en üst satırında ki orta hücreyi bularak başlayın ve hücrenin içine 1 yazın. Sonraki sayıları eğer yer varsa bir önceki sayının hep sağ üst çaprazındaki hücreye yazalım. Ancak 1’den sonra 2 sayısı için sağ üst çaprazda yer olmadığından, 2’yi sağdaki sütunun en altındaki hücreye yerleştirelim. Sonra 3 sayısını 2’nin sağ üst çaprazındaki hücreye yazalım.
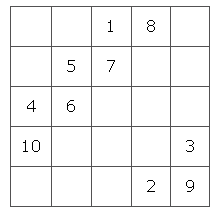
Şimdi 4 sayısını yerleştirmeliyiz fakat 3’ün sağ üst tarafında yerimiz yok. Bu durumda sağdaki son sütundan sonra soldaki ilk sütun devam edeceğiz. 5 sayısını ise 4’ün sağ üst çaprazına yazıyoruz. Ancak 6 sayısını 5’in sağ üst çaprazına yazamayız. Bu durumda 6 bir önceki sayının hemen altında yer almalı. Şimdi 7 sayısını 6’nın sağ üst çaprazına, 8’i ise 7’nin sağ üst çaprazına yerleştirelim.
9 sayısını 8’in sağ üst çaprazında hücre bulunmadığı için son sütunun en alt satırına yazalım. Aynı şekilde 9’un sağ üst çaprazında yer olmadığı için 10 sayısını ilk sütunun dördüncü satırına yerleştirelim. 11 sayısını 10’un hemen altındaki hücreye yazalım. Diğer sayılarımızı sırasıyla bir önceki sayının sağ üst çaprazındaki hücreye yerleştirelim.
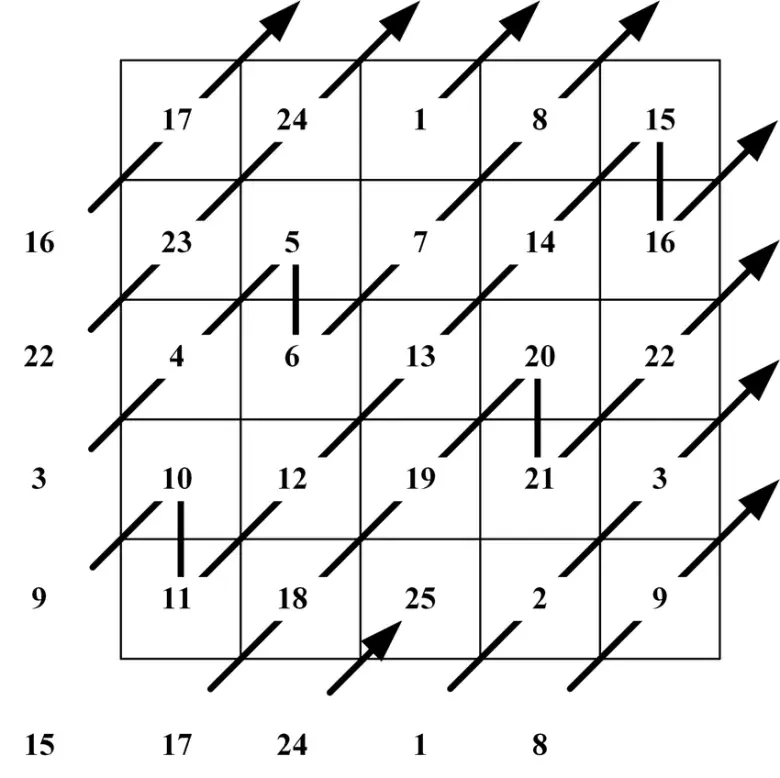
16 sayısını 15’in hemen altına yazalım. Daha sonra 17, 18, 19 ve 20 sayılarını önceki sayılarda olduğu gibi yerleştirelim. Sonuçta diğer sayıları da aynı mantıkla yerleştirdiğiniz zaman sihirli kareniz yukarıdaki gibi olacaktır.
Tek Ve Çift Dereceli Sihirli Kareler Nedir?
Sihirli kareler, kenarlardaki hücre sayısının tek veya çift oluşuna göre de isimlendirilebilir. Yukarıda aktardığımız yöntemle tek sayılı sihirli bir kare oluşturmak kolaydır. Ancak aynı şeyi çift dereceliler için söylememiz olası değildir. Aslına bakarsanız sadece n sayısı dördün katı ise, nxn boyutlarında sihirli kareler elde edebiliyoruz.
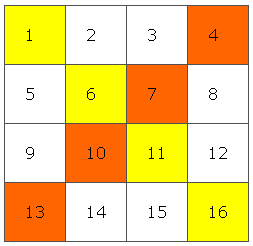
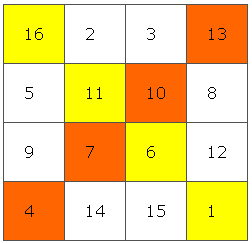
Şimdi 4×4’lük bir sihirli kare yapalım. Bunun için öncelikle hücreleri yukarıdaki gibi numaralandırın. Ardından ana köşegenlerinde bulunan sayıları işaretleyin. Şimdi 1 ile 16, 4 ile 13, 6 ile 11, 7 ile 10 biçiminde köşegenlerdeki sayıları birbiri ile değiştirin.
Elde ettiğiniz bu sihirli kare, başta bahsettiğimiz Alman sanatçı Albrecht Dürer’in çizdiği ile aynıdır. Gravür Melencolia’nin köşesinde görebilirsiniz.
Latin Kareleri Nedir?
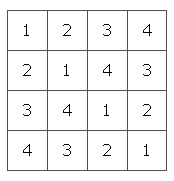
Latin kareleri Sudoku’nun gerçek atalarıdır. Sayılar, harfler ve sembollerle oluşturulur. Latin kare ve sihirli kare arasındaki fark kullanılan sembollerin sayısıdır. Örneğin 4×4’lük bir sihirli kare için 16 farklı sayı kullanılır. Oysa 4×4 lük bir latin kare için yalnız 4 farklı sayı gerekir. Bunun bir örneğini aşağıda görmeniz mümkündür.
Bazen Latin kareleri birleştirmek gerekir. Bu tür karelere Greko-Latin kareler denir. Aynı zamanda Euler kareleri olarak bilinirler. Greko-Latin karesi, dik Latin karelerinin birleşimi olarak da tanımlanır. Detaylar için: Euler’in 36 Subay Problemi ve 243 Yıl Sonra Gelen Tuhaf Çözümü
Sudoku veya Su Doku, Latin karelerinin özel bir türüdür. Genellikle 9x9luk kare ızgara şeklindedir ve küçük 3×3’lük kutulara bölünürler. Bildiğiniz gibi oyunun amacı, 1’den 9’a kadar olan her bir sayı ile bütün hücreleri doldurmaktır. Böylece her sayı tam olarak her sıra, sütunda ve 3×3’lük kutularda bir kez görünür.
Görüldüğü gibi uzun yıllar boyu büyücülerin, kahinlerin tekelinde kalan sihirli kareler matematikçilerin ilgi alanına girdikten sonra çok farklı bir boyut kazanmıştır. Bugün bile çoğu amatör olmak üzere birçok matematikçi sihirli karelerle ilgilenmekte ve bu konuda çalışmalar yapmaktadır.
Kaynaklar ve ileri okumalar:
- Anything but square: from magic squares to Sudoku; Yayınlanma tarihi: 1 Mart 2016; Bağlantı: https://plus.maths.org/
- The maths of magic squares; Yayınlanma tarihi: 15 Temmuz 2014; Bağlantı: https://plus.maths.org/content/maths-magic-squares-0?
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel











Hesaplarınız ve anlatımınız harika
Teşekkür ederim. Keyifli okumalar :)