Hepimiz çarpma işlemini temel düzeyde nasıl yapacağımızı biliriz. Örneğin sizden 691 ile 389’u çarpmanız istendi. Çoğu insan gibiyseniz, ilk iş olarak telefonunuzun hesap makinesine yönelirsiniz. Ancak teknolojik bir yardım elinizin altında yoksa ya da işlemi kendiniz yapmanız gerekiyorsa, muhtemelen ilkokulda öğrendiğiniz klasik çarpma yöntemini kullanırsınız. Bu yöntem, sayıları alt alta yazarak basamak basamak çarpma ve ardından bu ara sonuçları toplama esasına dayanır. Aşağıda bu yöntemin nasıl uygulandığını adım adım görebilirsiniz
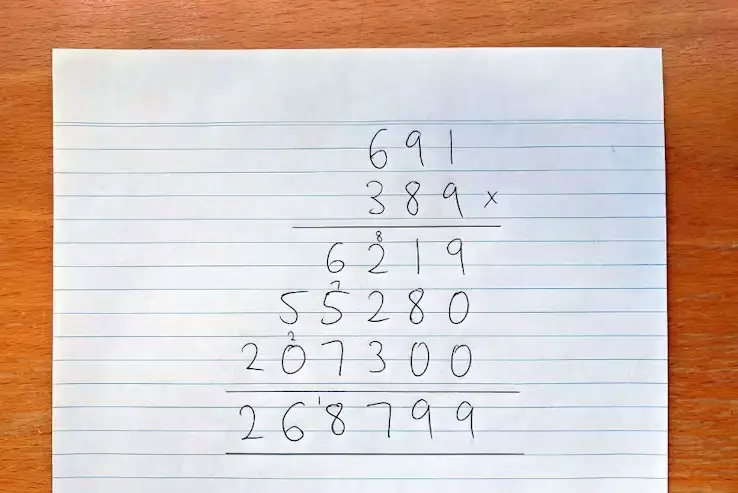
İlköğretimde öğrendiğimiz bu çarpma yöntemi, özellikle küçük sayılar için oldukça pratiktir ve hata payı düşüktür. Bu yöntemde, alttaki sayının her basamağını üstteki sayıyla tek tek çarparız. Ardından elde edilen ara sonuçları toplarız. Bu işlem basittir ama sayıların basamakları arttıkça, işlem yükü de hızla artar.
Her iki sayı da N basamaklı ise, bu yöntemde yaklaşık N² adet çarpma işlemi yapılması gerekir. Örneğin, yukarıdaki örnekte her iki sayı da 3 basamaklı olduğu için 3 × 3 = 9 ayrı çarpma işlemi yeterlidir. Ancak sayılar büyüdükçe durum değişir.
100 basamaklı iki sayıyı çarpmak için 10.000 çarpma işlemi, bir milyar basamaklı iki sayı için ise 10¹⁸ işlem gerekir. Bu büyüklükteki işlemler, günümüz bilgisayarları için bile ciddi bir zaman ve kaynak sorunu oluşturur. Öyle ki, bir milyar basamaklı iki sayının bu yöntemle çarpılması, güçlü bir bilgisayarın yaklaşık 30 yılını alabilir.
Peki bu gerçekten en iyi yöntem mi? Binlerce yıl boyunca çarpma işlemini hızlandırmanın daha iyi bir yolu olmadığı sanıldı. Ta ki 1960 yılında, henüz 23 yaşında olan Rus matematikçi Anatoly Karatsuba, 20. yüzyılın en büyük matematikçilerinden biri olan Andrey Kolmogorov’un verdiği bir seminere katılana kadar.
Karatsuba Yöntemi İle Çarpma İşlemi Nasıl Yapılır?
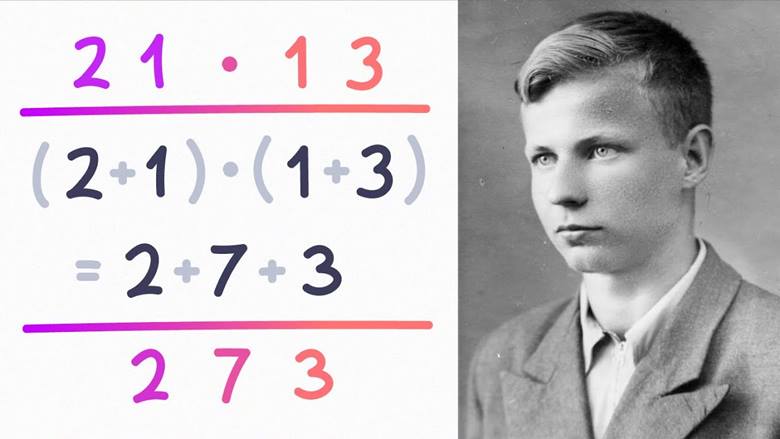
Kolmogorov, genel anlamda bir çarpma işleminin n² adımdan daha azıyla yapılamayacağını savunuyordu. Karatsuba ise bunun mümkün olabileceğini düşündü. Bir hafta süren yoğun bir çalışmanın ardından, gerçekten de daha hızlı bir yöntem buldu.
Karatsuba’nın yöntemi, sayıların basamaklarını bölerek ve bu parçaları alışılmadık bir şekilde yeniden birleştirerek, çok sayıda çarpma işlemini daha az sayıda toplama ve çıkarma işlemiyle değiştirmeyi içerir. Bu yöntem zaman kazandırır çünkü toplama işlemi yalnızca yaklaşık 2n adım gerektirirken, klasik çarpma yöntemi n² adım ister. Bunun nasıl yapıldığını anlamak için aşağıdaki görseli incelemenizi öneririz.
Normalde, iki n basamaklı sayıyı çarpmak için klasik (ilkokulda öğrendiğimiz) yöntemde yaklaşık n × n = n² tane tek basamaklı çarpma yapmamız gerekir. Yani 3 basamaklı iki sayı için 9, 1000 basamaklı iki sayı için 1 milyon adet çarpma işlemi gerekir.
Ancak Karatsuba algoritması, bu çarpma işlemlerinin sayısını azaltır. Sayıları parçalara ayırarak bazı çarpmaları toplama ve çıkarma işlemleriyle değiştirir. Böylece yapılması gereken çarpma işlemi sayısı kabaca n^1.585 (yaklaşık olarak n üzeri 1.58) seviyesine düşer.
Bu fark ilk bakışta çok büyük görünmez. Ancak basamak sayısı arttıkça avantajı açıkça ortaya çıkar. Örneğin klasik yöntemle örneğin n = 1000 için 1.000.000 çarpma işlemi yapmak gerekir. Oysa ki Karatsuba yöntemi ile n = 1000 için yaklaşık 38.000 çarpma işlemi yapmak gerekecektir. Bu da işlem süresinde büyük bir kazanç anlamına gelir. Peki biri neden böyle büyük sayıları çarpmak istesin?
Cevap, güvenlik. İnternette her şifreli iletişim kurduğunuzda—örneğin bir bankaya giriş yaptığınızda, bir mesaj uygulaması kullandığınızda ya da alışveriş yaptığınızda—cihazınız arka planda yüzlerce, hatta binlerce basamaklı sayıları çarpmak zorundadır. Bu, modern şifreleme algoritmalarının temelini oluşturur.
Çarpma İşlemini Daha Hızlı Yapmak İçin Yeni Yöntemler
Karatsuba, 1960 yılında bu kapıyı açtığından beri, matematikçiler daha da hızlı yöntemler geliştirmeye devam ediyor. 1971’de Arnold Schönhage ve Volker Strassen, çok daha verimli bir yöntem yayımladı: n × log n × log(log n) adımda çarpma yapabilen bir algoritma. Bu farkın büyüklüğü, örneğin iki 1 milyar basamaklı sayıyı çarpmak istediğinizde ortaya çıkıyor. Karatsuba yöntemi yaklaşık 165 trilyon fazladan adım gerektirirken, Schönhage–Strassen algoritması bunu çok daha hızlı tamamlayabiliyor.

Bu yöntem, hızlı Fourier dönüşümü (FFT) adı verilen ve sinyal işleme alanından alınmış bir tekniği ilk kez bu alanda kullandı. Bu teknik, o günden bu yana geliştirilen tüm hızlı çarpma algoritmalarının temelini oluşturdu. Bu yöntemin iki önemli kalıcı etkisi oldu:
- FFT’nin kullanılması: Fourier dönüşümünün hızlı versiyonu, çarpma algoritmalarına ciddi bir hız kazandırdı ve matematikte yeni bir çağ başlattı.
- Daha iyi bir algoritma olabileceği fikri: Schönhage ve Strassen, makalelerinde kendi algoritmalarından bile daha iyi bir çarpma yöntemi olması gerektiğini öne sürdü. Bu varsayım, işlemin temel doğası gereği n × log n gibi daha zarif ve estetik bir karmaşıklık sınırının olması gerektiği düşüncesine dayanıyordu.
Schönhage ve Strassen’in önerisi, sadece teknik bir iyileştirme değil, aynı zamanda matematiğin doğasına dair bir sezgiydi: Temel işlemlerin karmaşıklığı da temel kadar sade olmalıydı. Bu varsayım, yaklaşık 50 yıl sonra Harvey ve van der Hoeven tarafından geliştirilen algoritmayla gerçeğe dönüştü. Onlar, gerçekten de n × log n adımda çarpmanın mümkün olduğunu matematiksel olarak ispatladılar. Bu, Schönhage ve Strassen’in 1971’de yaptığı öngörünün doğruluğunu ortaya koydu.
Çarpma İşlemi İçin Bir Sınıra Ulaştık mı?
Schönhage ve Strassen’in çarpma algoritması, tam 36 yıl boyunca en hızlı bilinen yöntem olarak kaldı. Ta ki 2007’de Martin Fürer, bu yöntemi geçene kadar. Fürer’in başarısıyla birlikte matematik dünyasında bir kapı açıldı. Sonraki on yılda, matematikçiler giderek daha hızlı algoritmalar geliştirdiler. Bu sayede de n × log n sınırına adım adım yaklaştılar. Ama tam olarak ulaşamamışlardı.
Ta ki 2023’te David Harvey ve Joris van der Hoeven bu sınırı matematiksel olarak aşmak değil ama tam olarak yakalamayı başarana kadar. Yeni algoritmaları, kendilerinden önceki büyük çalışmaların bir devamı niteliğinde.
Sayıları yine parçalara ayırıyorlar. Ama bu kez çok daha gelişmiş bir hızlı Fourier dönüşümü (FFT) versiyonu kullanıyorlar. Ayrıca son kırk yılda yapılan başka matematiksel ilerlemeleri de entegre ediyorlar.
Harvey ve van der Hoeven’in algoritması, matematiksel olarak büyük bir başarı olsa da, günlük hesaplamalarda ya da standart yazılımlarda devrim yaratmayacak. Ancak çarpma işleminin teorik sınırlarına ulaşılması, temel matematik açısından tarihi bir dönüm noktası olarak kabul ediliyor.
Kaynaklar ve İleri Okuma:
- Mathematicians Discover the Perfect Way to Multiply. Yayınlanma tarihi: 11 Nisan 2019; Kaynak site: Quanta Magazine. Bağlantı: Mathematicians Discover the Perfect Way to Multiply/
- This Guy Just Found a Faster Way to Multiply. Yayınlanma tarihi: 19 Ekim 2019. Kaynak site: Popular Mechanics. Bağlantı: This Guy Just Found a Faster Way to Multiply/
- On Your Mark, Get Set, Multiply. Yayınlanma tarihi: 23 Eylül 2019. Kaynak site: Quanta Magazine. Bağlantı: On Your Mark, Get Set, Multiply/
- Schönhage, A., Strassen, V. Schnelle Multiplikation großer Zahlen. Computing 7, 281–292 (1971). https://doi.org/10.1007/BF02242355
- Fürer, Martin. (2009). Faster Integer Multiplication. Proceedings of the Annual ACM Symposium on Theory of Computing. 39. 10.1137/070711761.
Matematiksel






