Hepimiz sosyal medya kullanıyoruz. Bu süreçte de bir çok kısa, anlık cevap verilmesi gereken matematik ya da akıl yürütme soruları ile karşılaşıyoruz. Bu sorular genellikle sıralı bir kaç sayıdan sonra “Dizideki bir sonraki sayı nedir” biçiminde başlıyor.
Amaç sayılar arasındaki kuralı yani örüntüyü bulmak ve sonraki sayıyı elde etmektir. Bir kaç örnek mi istiyorsunuz. Elbette. Aşağıdaki dizilerde bir sonraki sayı nedir?
- 1, 3, 5, 7, 9, 11…
- 1, 4, 9, 16, 25, 36…
- 1, 2, 4, 8, 16…
Şimdi cevaplara geçelim. Sizin de tahmin ettiğiniz gibi ilk dizimiz tek sayılardan oluşuyordu. Bu nedenle sıradaki sayımız 13 olmalıdır. İkinci dizimiz kare sayılardan oluşuyor. Bu nedenle bir sonraki sayımız 49 olacak. Son dizimiz de 2 sayısının kuvvetlerinden oluşuyor. Bu nedenle aradığımız bir sonraki sayı 32 olmalı. Emin misiniz? Cevabını evet ise lütfen kesin emin olmayın.
Matematikte Genelleme Yapmak Kolayca Tuzağa Düşmenize Neden Olacaktır?
Fikir, dizinin terimlerinin üretildiği kuralı diğer adıyla örüntüyü tespit etmektir. Ancak bu örüntü temelinde hiçbir zaman ilk birkaç terim tarafından belirlenmez. Aslına bakarsanız bu nedenle bugüne kadar sorulmuş bir çok örüntü ya da bir sonraki sayıyı bul sorusu hatalıdır. Bunun nedenini son sayı dizimiz olan 1, 2, 4, 8, 16…üzerinden aşağıdaki örnekler ile aktarmaya çalışalım. Sonucunda baktığınız zaman cevap bariz bir biçimde 32 gibi gözüküyor. Ancak bu kesinlikle öyle olması gerekiyor anlamına da gelmiyor.
Oluşan Bölge Sayısını Bulalım
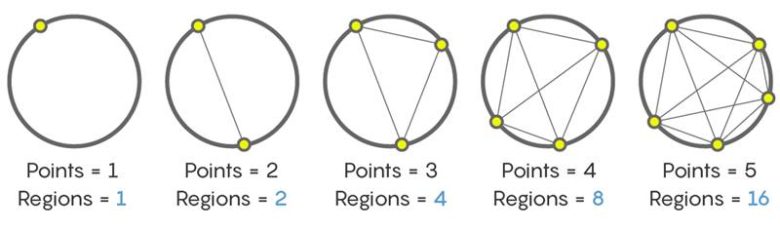
Sorumuz bir çember üzerindeki noktaları birleştirerek oluşturulan bölgelerin sayısını bulmak olsun. Bunu aşağıdaki yukarıda şekil üzerinden bulmaya çalışalım. Çember üzerinde aldığımız bir nokta 1 bölge oluştururken (çemberin iç bölgesi), çember üzerinde alınan farklı iki nokta 2 bölge oluşturur. Devamında üç noktadan 4 bölge meydana gelecektir. Dört ve beş nokta da, sırasıyla 8 ve 16 bölge oluşturur.
Böylece az önce bahsettiğimiz 1, 2, 4, 8, 16 sayı dizisine geri dönüyoruz. İçgüdülerimizde haklı olduğumuz hissi biraz daha pekişti öyle değil mi? Peki, çember üzerinde alınan birbirinden farklı altı nokta birleştirilirse kaç tane bölge oluşur? Ne yazık ki cevap 32 değil. Bir sonraki sayı 31 olacaktır. Bize inanmıyorsanız aşağıdaki çözüme göz atabilirsiniz. Emin olmak için elbette saymayı da deneyebilirsiniz.
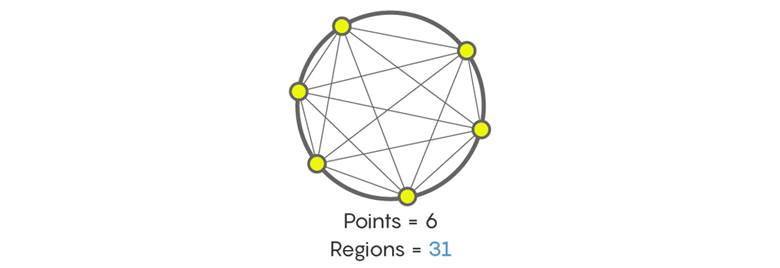
Yukarıdaki örneğimiz sizi şaşırttı ise daha da çok şaşırabilirsiniz. Elbette 1, 2, 4, 8, 16, 32, 64… ve benzeri şekilde ikiye katlayarak artan örüntüler vardır. Ancak gördüğünüz gibi 1, 2, 4, 8, 16, 31, 57, 99… biçiminde devam eden örüntüler de vardır. Bu nedenle bir sonraki sayı nedir? dediğimiz zaman tek bir cevabı beklememiz bir yanılgıdır. Bu nedenle matematikçiler sürekli olarak bir kanıtın peşinde koşar. Sonucunda kanıtlayabildiğiniz zaman varsayımlar ortadan kalkacaktır.
Genelleme Hatasına Bir Başka Örnek
“Herhangi iki doğru kesişir veya paraleldir.” söylemini araştırmak istediğinizi düşünün. Bu iddiayı denemek için aklınıza bir model oluşturmak gelebilir. Bu model de muhtemel hepimizin tanıdığı y=mx+n biçiminde olacaktır. Burada m doğrunun eğimini n ise y eksenini kestiği noktayı temsil eder. Şimdi rastgele sayılar seçerek rastgele çizgiler çizelim ve kesişip kesişmediklerini kontrol edelim. İşte bazı örnekler.
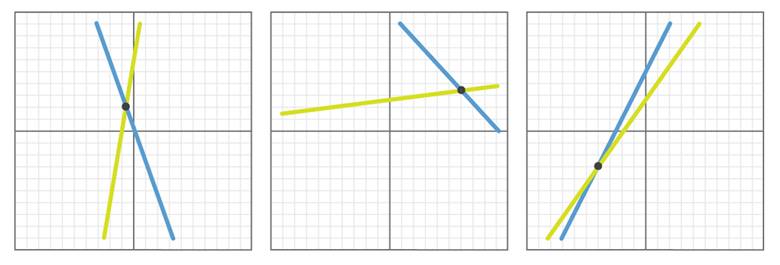
Yukarıdaki her örnekte rastgele seçilen çizgilerin kesiştiğini görüyoruz. Bu deneyi 1.000 kez – veya 10.000 kez veya 1 milyon kez – denersek ve her seferinde yukarıdaki gibi kesişen çizgiler çıkarsa varsayımın muhtemelen doğru olduğu sonucuna varabilirsiniz. Sonucunda elinizdeki kanıtlar bunu desteklemektedir.
Ancak aynı az önceki bir sonraki sayı örneğimizde olduğu gibi bir kere daha matematiksel bir düşünce hatası yaparsınız. Öncelikle 1’den büyük bir sayı seçmek, 0 ile 1 arasında bir sayı seçmekten çok daha olasıdır. Bu, belirli türdeki çizgilerin (eğimi 0 ile 1 arasında olanların) modelimizde oldukça az temsil edilebileceği anlamına gelir.
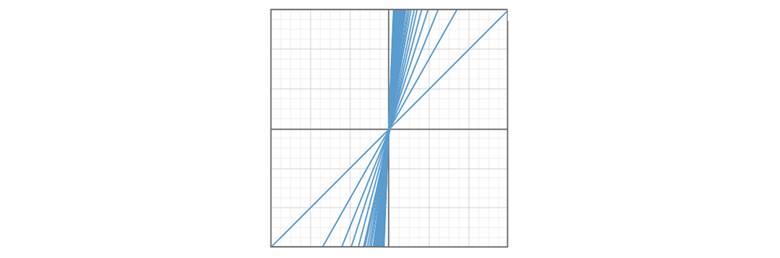
Grafiğe daha yakından bakıldığında başka bir sorun ortaya çıkıyor. Sonucunda m büyüdükçe çizgiler de dikleşir. Mümkün olan en dik çizgi ise dikeydir ve tanım gereği dikey bir doğrunun eğimi tanımsızdır. Bu, bu çizgilerin modelimizde bulunmadığı anlamına gelir. Son ve en önemli sorunu muhtemel fark etmişsinizdir. Sonucunda aşağıdaki görselde gördüğünüz gibi kesişmeyen ve paralel olmayan çizgiler de vardır.
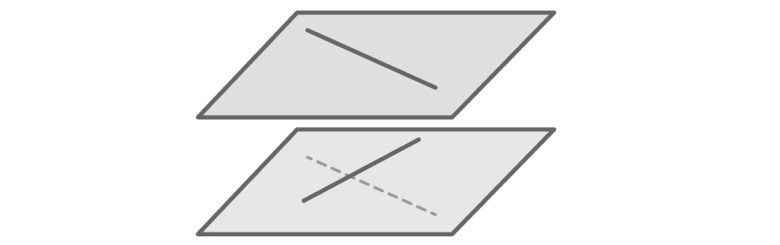
Sonuç Olarak
Sonuç olarak yukarıdaki örneklerde de gördüğünüz gibi bazı varsayımlar matematiksel hatalar yapmamıza neden olacaktır. Neyse ki matematikçiler bu durumun farkındadır. Bu nedenle içgüdüleri ne kadar ikna edici olursa olsun, arka planda hayal bile edemedikleri bir şey olduğunu bilirler. Bu nedenle de genelde içgüdülerine fazla güvenmezler. Bir sonraki zeka sorusunu çözerken bunların da aklınızda bulunmasını öneririz.
Yazımızın bitiminde ayrıca göz atmak isterseniz: Kolakoski Dizisi: En İlginç Sayı Dizilerden Birisi İle Tanışın
Kaynaklar ve ileri okuma:
- Where Proof, Evidence and Imagination Intersect; Yayınlanma tarihi: 14 Mart 2019; Kaynak site: Quanta Magazine. Bağlantı: Where Proof, Evidence and Imagination Intersect
- What’s the Next Number? yayınlanma tarihi: 24 Kasım 2022; Bağlantı: https://thatsmaths.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel