Antik çağda geometrinin en önemli sorunlarından bir tanesi sadece işaretli olmayan bir cetvel ve pergel kullanarak verilen bir açıyı üç eşit parçaya bölme ile ilgiliydi. Bu problemi çözme çabalarında da bir dizi dahiyane eğri icat edilmişti. İşte bu eğrilerden bir tanesi de Ellisli Hippias tarafından bulunmuştur.
Çözümsüz soruların cazibesi, matematiğin can damarıdır. Bu nedenle sayılar teorisi veya soyut cebir matematikçilerin en sevdiği konuların başında gelir. Çoğu zaman, bir sorunun çözümü yenilerini ortaya çıkarır. Bu şekilde de sonu asla gelmeyecek bu süreç devam eder.
Matematik problemi çözmeye sadece günümüz matematikçilerinin takıntılı olduğunu düşünüyorsanız aslında yanılıyorsunuz. Aynı durum Antik Yunanlılar zamanında da geçerliydi. Özellikle üç problem o dönemin düşünürlerini uzun süre meşgul etmişti. Bu problemler günümüzde antik çağın üç problemi olarak bilinmektedir

M.Ö. beşinci yüzyılın sonlarına doğru Atina’da adlarına Sofistler dediğimiz halka açık özel dersler vererek maddi kazanç sağlayıp yaşamını sürdüren bir grup profesyonel öğretmen ortaya çıktı. Bu öğretmenlerden biri de Ellis’li Hippias’dır. Kendisi kuadratriks ( Quadratrix ) eğrisi vasıtasıyla açıyı üçe bölen mekanik bir çözüm geliştirmiştir. Çalışması hareketli parçalar tarafından oluşturulan bir kinetik eğri örneğidir.
Kuadratriks Eğrisi İle Açıyı Üçe Bölme
Hippias işe öncelikle bir kare çizmekle başlamış. Sonrasında bu kare içerisine karenin bir kenar uzunluğu yarıçapında köşesi karenin bir köşesi olan çeyrek çember çizmiş.
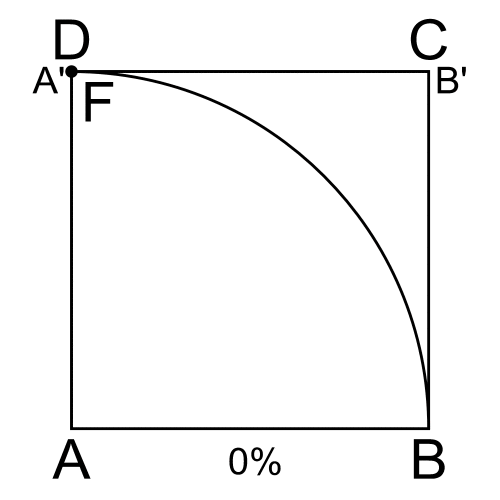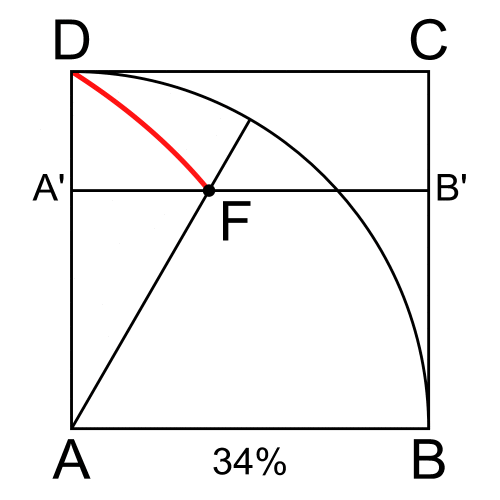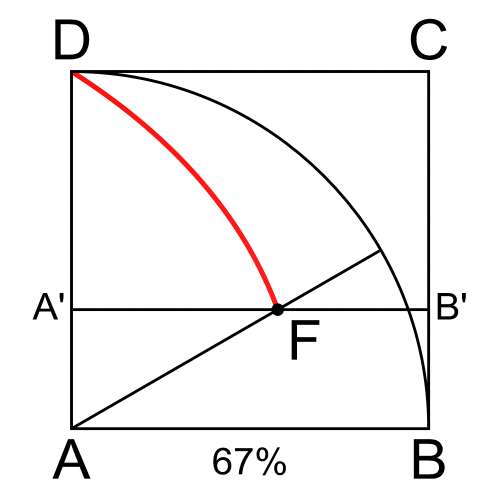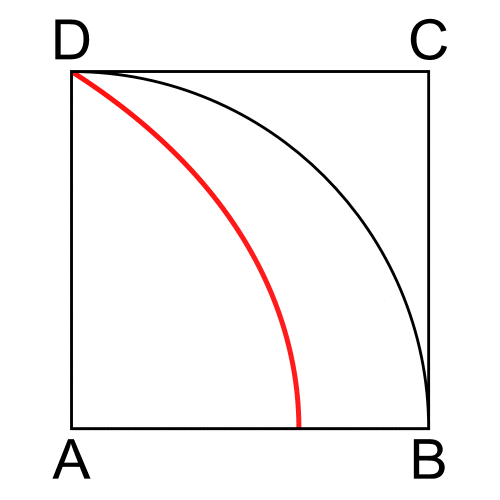
Herhangi bir oranda eşit parçalara bölünecek açı ABC olsun. Şimdi AB doğru parçasını BC doğru parçasına paralel kalmak üzere düzgün bir hareketle aşağı doğru kaydırıralım. Aynı zamanda, DA doğru parçasını da D noktası sabit kalmak üzere saat ibresi yönünde yine düzgün bir hareketle döndürelim.
Bu düzgün hareketler sonunda DA doğru parçası ile AB doğru parçalarının kesim noktalarının geometrik yeri Hippias’ın kuadratriks eğrisidir. Bu yay yardımıyla her açı istenilen oranda eşit parçalara bölünecektir. Yukarıdaki animasyonda bunu daha net bir biçimde görebilirsiniz.
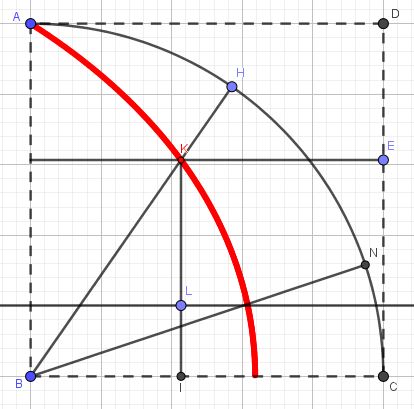
Amacımız HBC açısını üçe bölmek olsun. HB doğru parçasının kuadratriksi kestiği nokta olan K noktasından BC ye bir dikme indirelim. İndirdiğimiz dikme olan KI doğru parçasını üç eş parçaya bölelim. Biraz geometri bilgisi ile şu eşitliği yazabiliriz:
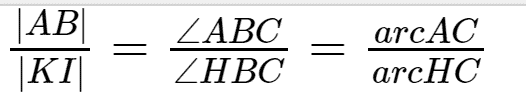
L noktasından tabana paralel olarak çizilen doğru parçasının kuadratriksi kestiği nokta ile B noktası birleştirildiğinde oluşan NBC açısı HBC açısının üçte biri olacaktır. Dolayısıyla HBC açısını üçe bölme görevini tamamlamış olduk.
Hippias’ ın bulduğu bu eğri ile verilen bir açıyı istenen oranda eşit açılara bölmesinden bir kaç yıl sonra, Dinostratus bu eğriyi dairenin alanını kareleştirmede kullanmıştır. Gerçekten, bu eğriyle dairenin alanına eşit bir kare çizme olanağı vardır. Dikkat edilirse, Hippias’ın eğrisi yalnız pergel ve ölçüsü olmayan cetvelle çizilecek türde değildir. Bu nedenle çözüm Platon tarafından kabul edilmemiştir.
Kaynaklar ve ileri okumalar:
- Matematik Tarihi, David M. BURTON (çev. edt. Prof. Dr. Soner DURMUŞ)
- Heilbron, J.L.. “Trisecting the Angle: The Quadratrix of Hippias”. Encyclopedia Britannica, 27 Apr. 2001, https://www.britannica.com/topic/Trisecting-the-Angle-The-Quadratrix-of-Hippias-1688521. Accessed 22 May 2024.
- Quadratrix of Hippias; https://en.wikipedia.org/wiki/Quadratrix_of_Hippias
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel







Yazabiliriz dediğiniz eşitlik nerede , bunu bir deklemle ifade edersek dediğiniz denklem nerede ?
Bu arada ; denklem= eşitlik
Mükemmele yakın bir şekilde açıyı üçe bölme yöntemini biliyorum. Mükemmel mi değil mi bi bakmak isteye bilirsiniz belki 🙂