Matematik problemi çözmeye sadece günümüz matematikçilerinin takıntılı olduğunu düşünüyorsanız aslında yanılıyorsunuz. Aynı durum Antik Yunanlılar zamanında da geçerliydi. Özellikle üç problem o dönemin düşünürlerini uzun süre meşgul etmişti.

Bu problemler günümüzde antik çağın üç problemi olarak bilinmektedir. Bu problemler çok da şaşırtıcı olmayan bir biçimde geometri ile ilgilidir. Ancak bu üç problem ile ilgili detaylara geçmeden önce sizlere bir hatırlatma yapmamız gerekiyor.
Birazdan okuyacağınız problemlerden bazılarını örneğin açıyı üçe bölme problemini günümüzde kolayca çözebilirsiniz. Ancak problemlerin antik çağa ait olduğunu anımsayın. Bu nedenle elinizde modern döneme ait geometrik araçlarınız yok. Sadece bu da değil. Sadece ölçüsüz cetvel ve pergel kullanabilirsiniz.
Ölçüsüz cetvel ve ile sadece verilen iki noktayı birleştiren bir doğru çizebiliriz. Pergel ile de merkezi ve yarıçapı verilen bir çember çizebiliriz. Bu iki aletin bunlar dışında kullanımına izin yok. Bu arada son bir şart olarak da bu iki aracı, yalnızca Öklid’in ilk üç önermesinin kuralına göre kullanmanız mümkün. Şimdi o dönemim matematikçilerinin sorunlarını anladıktan sonra problemlerimize geçebiliriz.

Antik Çağın Üç Klasik Problemi Nedir?
1.Çemberin Karelenmesi:
Bilinen dünyanın belki de ilk problemlerinden biri, çemberi karelemek, yani bir daire ile aynı alana sahip bir kare elde etmektir. Antikçağda daire, gökcisimlerinin yörüngesinin şekli olduğu düşünülen tanrısal ve kutsal nitelikli kusursuz bir şekil olarak görülüyordu.
Kare ise Dünya’yı ve dünyasal yaşamı simgeliyor ve gökle yer arasında “insan” yer alıyordu. Dolayısıyla dairenin kareye dönüştürülmesi uğraşı, tanrısal/göksel/ruhsal olanın insansal/yersel/maddesel olana dönüştürülmesini de hedeflemekteydi.
Tüm çemberlerin çevrelerinin çaplarına oranının sabit bir sayı olduğu çok eski çağlardan bu yana bilinmekteydi. Bununla beraber bu sayının tam değerine ulaşmak oldukça güçtü. Bilinen ilk yazılı kaynakta çözümü aranan çemberi kareleme problemi ise bu oranı bulma yollarından bir tanesiydi.

On dokuzuncu yüzyıla gelindiğinde matematikçiler bunun mümkün olmadığını ispatladılar. Ve bu ispat geometri değil cebir fikrini barındırıyordu. Şimdi nedenine göz atalım. Yarıçapı r olan bir dairenin alanı π x r2 dir. Aynı alana sahip bir karenin bir kenarı da a birim olsun. Bu durumda π x r2 = a2 olmalıdır. Buradan da a değerini hesaplamak için pi sayısının karekökünü almamız gerekir.
Yani sadece bu iki aracı kullanarak karekök pi uzunluğunu çizersek problem çözülmüş olur. Ama ne yazık ki bu mümkün değildir. Ferdinand von Lindemann tarafından 1882 yılında pinin aşkın bir sayı olduğu ve aşkın sayıların da sadece cetvel ve pergel yardımıyla çizilemeyeceğinin gösterilmesiyle bu serüven son bulmuş oldu.
2. Delos Problemi – Küpün Hacmini İki Katına Çıkartmak:
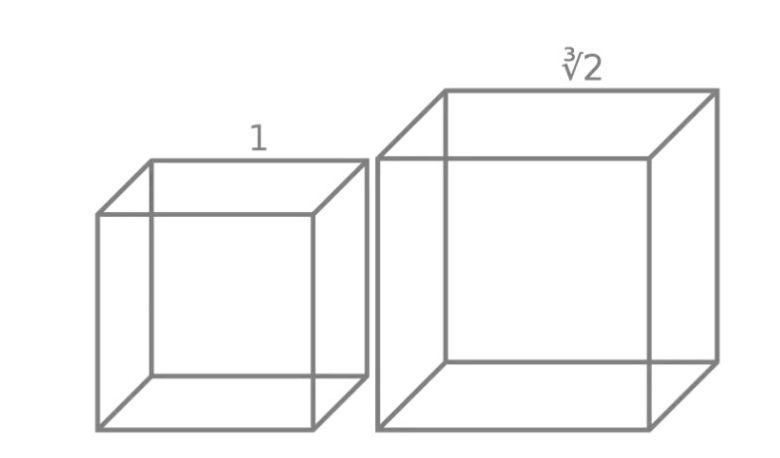
Ölçüsüz cetvel ve pergel ile verilen bir karenin alanını iki katına çıkarmak kolaydır. Bir kenarı a birim olan karenin alanının iki katına eşit olan bir kare çizmek istiyoruz. Karenin alanı a2 dir. Bizden istenen yeni karenin bir kenarı b birim olsun. Bu durumda b2=2a2 olmalıdır. Buradan da b=a√2 biçiminde olacaktır. O halde bize verilen bir a birim uzunluğundaki doğru parçasının kök iki katını çizebilirsek problem çözülmüş olur.
Verilen bir karenin alanının iki katına eşit olan bir kareyi bu araçlarla elde ettikten sonra, akla üç boyuta geçerek bu sorunun gelmesi gayet tabi bir durumdur. Lakin düzlemde başarılabilen uzayda başarılamamıştır.
Antik metinlerden bize aktarılan bilgiye göre Delos Problemi şöyle doğmuştur. Günümüzde Delos, Mykonos yakınlarındaki Ege Denizi’nin Kiklad Adaları’nda bir Yunan adası ve arkeolojik sit alanıdır. Ve bir zamanlar burada yaşayanlar bir sorun ile karşılaşmıştır. Bu sorun bölgede birdenbire ortaya çıkan bir veba salgınıdır.
Kent sakinleri hastalıktan korunmak için bir kâhine başvurur. Kâhin Delos Tapınağı’ndaki sunak taşının hacminin iki katına çıkarılması gerektiğini söyler. Bunun üzerine küp şeklindeki bu sunak taşını iki katına çıkarmak için mimar ve matematikçiler çalışmaya başlar. Ancak yukarıda aktardığımız sebepten dolayı da çabaları bir türlü sonuç vermez.

3. Bir Açının Üçe Bölünmesi:
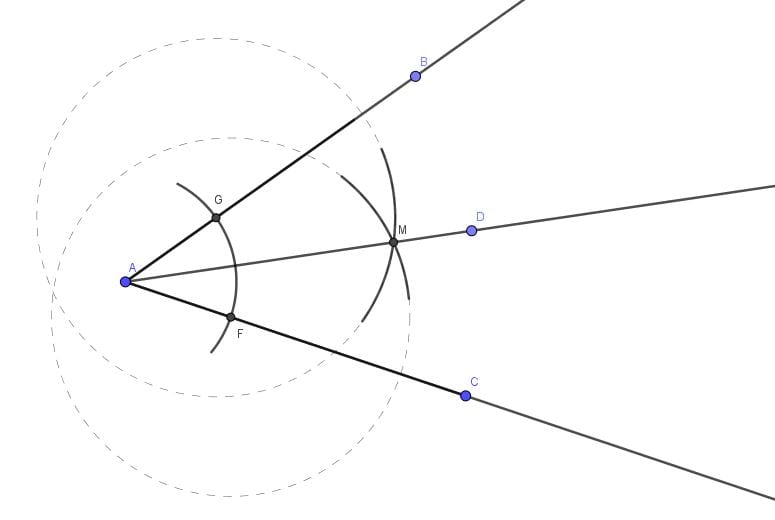
Açımız 90 derece olursa bunu yapmak zor değildir. Ayrıca ölçüsüz cetvel ve pergel ile herhangi bir açı çok kolay bir şekilde iki eş parçaya ayrılabilir. Aşağıdaki şekilde bunu görmek mümkündür. Peki üç eş parçaya ayrılması mümkün mü?
Elbette herhangi bir açıyı iletki kullanarak kolayca ölçebilir, elde ettiğiniz sayıyı 3’e bölebilir ve ardından iletki kullanarak açının istediğiniz üçte birini tekrar ölçebilirsiniz. Ancak mesele şu ki, iletki yasaktır. Genel bir açının üçe bölünüp bölünemeyeceği sorunu bin yıl boyunca matematiksel bir gizem olarak kaldı
Sonunda 1837’de Paris’teki Ecole Polytechnique’den Pierre Wantzel (1814-1848) herhangi bir açının sadece ölçüsüz cetvel ve pergel kullanılarak üçe bölünemeyeceği ile ilgili ilk formel ispatı verdi. Liouville’in Journal de Mathematiques dergisinde yayınlanan aynı makalede, Wantzel küpün iki katına çıkartılması probleminin anlamsızlığını da özel bir yöntemle gösterdi.
Antik Çağın Üç Problemi Neden Çözülememişti?
Bu sonucun anahtarı bu iki problemin denklemler teorisindeki sorulara dönüştürülmesiydi. Wantzel ölçüsüz cetvel ve pergelle inşa edilebilecek rasyonel katsayılı polinom bir denklemin çözümüne izin veren basit cebirsel kriterler elde etti. Klasik geometri problemleri olan açının üçe bölünmesi ve küpün iki katına çıkartılması Wantzel’in şartlarını sağlamayan bir kübik denklem vermektedir ve sonuç olarak söz konusu inşalar gerçekleştirilemez.
Artık biliyoruz ki, Antik Yunanlıların bu problemleri çözme girişimleri, başından itibaren başarısızlığa mahkumdu. Bunun nedeni bir şeyi gözden kaçırmış olmaları ya da işlerin yolunda gitmemesi değildi. Sadece günümüzde sahip olduğumuz sıradan hesaplama araçlarına sahip değillerdi.
Kaynaklar ve ileri okumalar:
- BURTON, M. David. Matematik Tarihi Giriş, (çev. editörü Prof. Dr. Soner DURMUŞ), Nobel;: Mart 2017
- Trisecting the angle with a straightedge; Yayınlanma tarihi: Bağlantı: https://plus.maths.org
- Rediske, Arthur. (2018). The Trisection of an Arbitrary Angle. JOURNAL OF ADVANCES IN MATHEMATICS. 14. 7640-7669. 10.24297/jam.v14i2.7402.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel