Rasyonel sayılar kümesi yoğun bir kümedir; yani birbirine ne kadar yakın olursa olsun, iki kesir arasında sonsuz sayıda kesir vardır. Buna karşın Rasyonel sayılar kümesi sayı doğrusunu tam olarak doldurmaz, aralarda boşluklar kalır. Bu boşlukları da İrrasyonel sayılar dolduracaktır. Üstelik İrrasyonel sayıların sayısı, Rasyonel sayıların sayısından kıyaslanamayacak derecede çoktur!

Pisagor sabiti 1.4142135623…’e eşittir.
Rasyonel ve İrrasyonel Sayılar Nedir?
Sayı doğrusu iki ana sayı sınıfına ayrılmıştır: kesirler olarak yazılabilen rasyonel sayılar ve diğer her şey olan irrasyonel sayılar. Tüm tam sayıları ve tam sayıların oranları olarak ifade edilebilen tüm kesirleri içeren rasyonel sayılar, günlük hayatta sıklıkla karşılaştığımız sayılardır.
Ayakkabı numaralarımız, fiyat etiketlerimiz, cetvel işaretlerimiz, basketbol istatistiklerimiz, tarif miktarlarımız — temelde ölçtüğümüz veya saydığımız her şey — rasyonel sayılardır. Ondalık gösterimde, rasyonel bir sayının gösterimi belirli sayıda basamaktan sonra sonlanır (örneğin, 3/4 = 0,75) veya tekrar eder (örneğin, 1/3, 0,333… olarak ifade edilir).
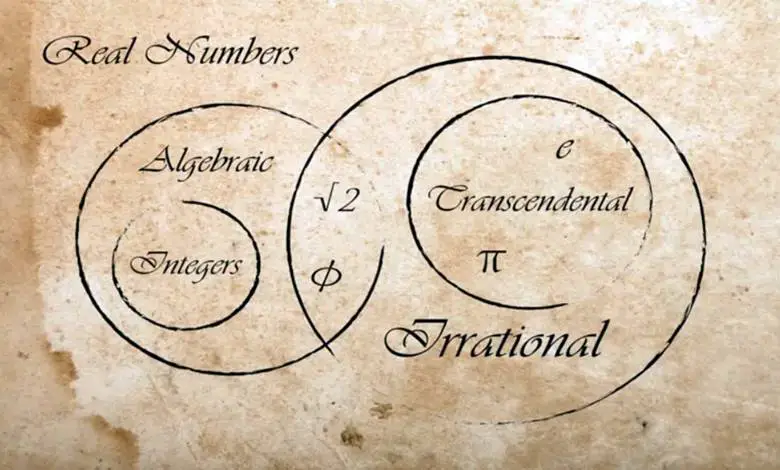
√2 ve π gibi irrasyonel sayılar, tam sayıların oranı olarak temsil edilemez. Ondalık gösterimleri asla sonlanmaz ve tekrarlamaz. Diğer bir deyişle a/b biçiminde ifade edilemeyen herhangi bir sayı irrasyonel bir sayıdır. Bu nedenle karekök 2 bir irrasyonel sayıdır. Çünkü bu sayıyı bir kesir ile gösterme şansımız yoktur.
Örneğin √2 sayısını bir hesap makinası yardımı ile hesaplarsak 1.41421356237309504880… gibi bir sonuç elde ederiz. Dikkat ederseniz rakamlar arasında hiçbir tekrar bulunmamaktadır. Şimdi de 1/109 kesrine bakalım.
1/109=0.0091743119266055045871559633027522935779816513761467889908256880733944954128440366972477064220183486238532110091743119266055045871559633027522935779816513761467889908256880733944954128440366972477064220183486238532110091743119266055045871559633027522935779816513761467889908256880733944955412844036697247706422018348623853211009174… biçiminde devam eder.
Kesrin ilk 100 basamağını hesapladığımızda herhangi bir tekrar görmeyiz. Bu, kesrin irrasyonel olduğu anlamına mı gelir? Hayır gelmez. Eğer hesaplamamızı 330 basamağa kadar götürürsek sayıda 108 rakamlı bir devir bulunduğunu buluruz. Oysa ki, bir irrasyonel sayıda böyle bir tekrar elde etmemiz mümkün değildir.
Bu sayıları anlamlandırmak ve hesaplamak için, genellikle onları yaklaşık olarak hesaplamamız gerekir. Örneğin, √2 kilometreyi tam olarak ölçemeyebiliriz, ancak 1,4 km. veya 1,414 km’yi ölçebiliriz ki bunlar da oldukça yakındır ancak tam karşılığı değildir. Aslında hesap makinesi ile hesapladığımızda elde ettiğimiz tüm cevaplar yaklaşık karşılıklarıdır.
Bu arada merak edilen bir soru Pi sayısının irrasyonel bir sayı olup olmadığıdır. Bunun nedeni aslında okullarda pi sayısının 22/7 biçiminde öğretilmesidir. Ancak 22/7 pi sayısı ile işlem yapmaya kolaylaştırmak adına kullanılan yaklaşık bir değerdir ve Pi sayısına eşit değildir.
İrrasyonel Sayıları Kim Buldu?

MÖ 5. yüzyılda Yunanistan’da, Sayıların babası” olarak bilinen Pisagor ve ona inananlar evrenin sayılardan yapıldığına inanıyordu. Pisagor’un sloganı, okulunun girişinin üzerine oyulmuştu. “All is number. ” yani “Her şey sayıdır”. Onlar bütün sayıların rasyonel olduğuna inanırlardı. Yani onlara göre tüm sayılar sadece ya sayma sayısıydı ya da iki sayma sayısının oranı olarak ifade edilebilirdi.
Ancak bir Yunan matematikçi matematiğin temellerini sarsan ve efsaneye göre hayatına mal olan bir keşif yaptı. Bazı tarihçilerin Metapontumlu Hippasus olduğuna inandığı bu matematikçi, her fiziksel olgunun tam sayılar ve onların oranları (şimdi rasyonel sayılar dediğimiz) cinsinden ifade edilebileceği temel ilkesini benimseyen Pisagor matematik okuluna mensuptu.

Hippasus bir dik üçgenin kenarlarının uzunluklarını düşündüğünde bu varsayımın çöktüğünü fark etmişti. Dik kenar uzunlukları 1 birim olan bir ikizkenar dik üçgende Pisagor Teoremi uygulandığında hipotenüsün uzunluğunu veren, yani karesi 2’ye eşit olan sayının iki sayma sayısının oranı olarak ifade edilemeyeceğini keşfetti.
Pisagorcular irrasyonel sayılar fikrinden hoşlanmamışlardı. Hippasus’un keşfinden dolayı öldürüldüğü söylenir ancak konu ile ilgili tarihsel kanıtlar oldukça belirsizdir. Hikayenin bir versiyonuna göre, Hippasus bu keşfi denizde yapmış ve dehşete düşen Pisagorcu arkadaşları onu denize atmışlardır.
Hippasus’un Karekök 2 sayısı İçin yaptığı İspat
Bu ispat matematik tarihinin en zarif kanıtlarından biridir. İspat bize √2 sayısının irrasyonel bir sayı olduğunu, yani bir kesir olarak yazılamayacağını gösterir.
Kendisi işe √2 sayısının rasyonel olduğu yani p / q biçiminde yazılabileceği fikri ile başlamıştı. (Burada p ve q sayılarının aralarında asal olduğunu yani sadeleşmediğini kabul ediyoruz.) Denklemin her iki tarafının karesi alındığında p2/q2=2, yani p2=2q2 olur. Buradan anlıyoruz ki p sayısı bir çift sayıdır.
O zaman bir k tamsayısı için p=2k yazabiliriz. Şimdi bunu denklemde yerine yazalım. 2q2=(2k)2=4k2olur. Gerekli sadeleştirme sonucunda q2=2k2 ifadesi bulunur. Bu durumda q2‘nin, dolayısıyla q’nun da çift olması gerekiyor.
Sonuçta ikisi de çift sayı ise sadeleşmeleri gerekir. Oysa biz başlangıçta bu sayıların aralarında asal olduğunu yani sadeleşmediğini kabul etmiştik. Bu, başlangıçtaki varsayımımızın yanlış olduğu anlamını taşır. Bu da irrasyonel olması gerektiği anlamına gelir.
Sonuç olarak
Modern matematikçiler, Yunanlıların irrasyonel sayılar konusundaki sıkıntılarının üstesinden geldiler (ve aslında rasyonel sayılardan çok daha fazla irrasyonel sayı olduğunu keşfettiler). Ancak Pisagorcu gelenek günümüzde halen sayılar teorisinin merkezinde yer alır ve tam sayı merkezli dijital çağımızda birçok uygulama alanı bulmuştur.
Kaynaklar ve ileri okumalar:
- What Are Irrational Numbers? Yayınlanma tarihi: 17 Aralık 2019. kaynak site: Live Science. Bağlantı: What Are Irrational Numbers?
- How Rational Math Catches Slippery Irrational Numbers. Yayınlanma tarihi: 10 Mart 2020. Kaynak site: Quanta Magazine. Bağlantı: How Rational Math Catches Slippery Irrational Numbers
- Agarwal, Ravi & Agarwal, Hans. (2021). Origin of Irrational Numbers and Their Approximations. Computation. 9. 29. 10.3390/computation9030029.
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





Çok güzel yazılar yazıyorsunuz, sizleri kutluyorum. Yukarıdaki sayı kök 2 değil kare kök 2 olduğunu hatırlatma cüretinde bulunabilir miyim?
Haklısınız, uyarınız için teşekkürler.
Bu kadar çorak iklimde matematiğin aydınlık dünyasından kesitler sunduğumuz için teşekkür etmeyi bir borç bilirim.
Saygılarımla.