Matematiksel sabitler arasında pi sayısı binlerce yıldır matematikçi olsun ya da olmasın insanları büyülüyor. Aynı zamanda 14 Mart tarihi 3/14 olarak yazıldığı için tüm dünyada Pi günü olarak kutlanıyor. Hatta aynı tarih Dünya Matematik günü olarak da kabul ediliyor. Öte yandan Pi sayısı sadece 3 ile 4 arasında yer alan herhangi bir sayı. Peki ama bir sayıya bunca ilgi neden kaynaklanıyor?
Hepimizin görmeye alışık olduğumuz Pi sembolü Yunanca çevre manasına gelen “περίμετρον” sözcüğünün baş harfidir. Ancak sayıyı bu şekilde temsil etme geleneği aslında Yunanistan’dan gelmiyor. 18. yüzyılın başında matematikçiler pi’yi 100’den fazla ondalık basamağa kadar doğru bir şekilde nasıl hesaplayacaklarını bulduktan sonra bile sayı için üzerinde anlaşmaya varılan bir sembolümüz yoktu.
Ancak bu durum matematikçi William Jones sayesinde değişti. Kendisi bu özel sayının kendi sembolüne ihtiyacı olduğunu fark etti. Bunun sonucunda da kaleme aldığı kitabında aşağıda gördüğünüz gibi ilk pi sembolünü kullandı.

Pi Sayısı Nedir ve Kaç Basamağını Biliyoruz?
Matematik sabiti pi (π), bir çemberin çevresinin çapına oranıdır ve yaklaşık olarak 3,1415926536’dır. Yalnızca bu on ondalık basamakla Dünya’nın çevresini bir milimetreden daha az hata payı ile hesaplamamız mümkündür. Sadece 32 basamakla gözlemlenebilir evrenin çevresini, en fazla bir hidrojen atomunun çapı kadar hata payıyla ölçebilirsiniz. Ve hatta pi sayısının 65 ondalık basamağı gözlemlenebilir evrenin boyutunu bir Planck uzunluğuna kadar hata payıyla ölçmemiz için yeterlidir.

Ancak 2021 yılında 108 gün ve 9 saat süren bir çalışmanın ardından İsviçreli bilim insanları Pi sayısının 62.8 trilyon basamağını süper bilgisayar ve 1988’de geliştirilen Chudnovsky algoritması adı verilen özel bir formül yardımı ile hesapladı. Peki bunca basamağı nerede kullanacağız? Kısa cevap, bunların bilimsel olarak hiçbir şekilde yararlı olmadığı olsa da, matematikçiler ve bilgisayar bilimcileri çeşitli nedenlerden dolayı Pi sayısının daha fazla basamağını hesaplamaya devam edecektir.
Pi Sayısı Neden Bu Kadar Önemlidir?
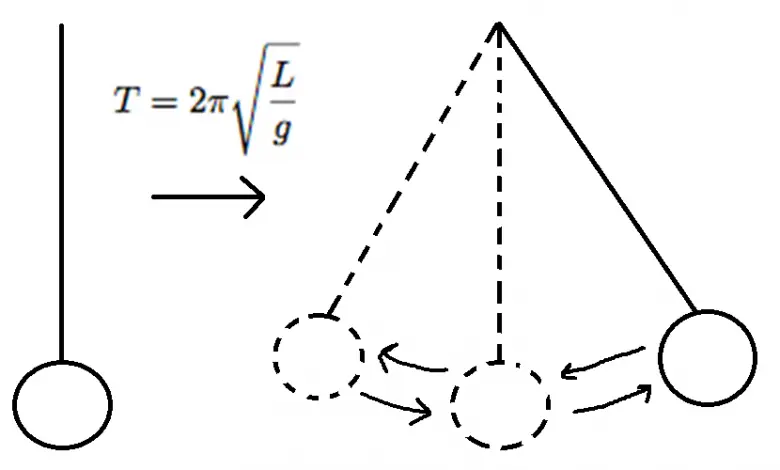
Çember ile ilişkili herhangi bir şey, kaçınılmaz olarak bu sabiti de içerir. Bununla birlikte, pi sayısı çember ile daha az ilişkili yerlerde de karşımıza çıkar. Örneğin, bir sarkacın hareketini, bir ipin titreşimini veya bir nehrin dolambaçlı desenlerini tanımlayan denklemlerde de vardır. Pi sayısının şaşırtıcı biçimde pek çok defa karşımıza çıkması da matematikçileri büyülemektedir. Örneğin akıllı telefonunuz Pi’yi içeren hızlı bir Fourier dönüşümü gerçekleştirmektedir.
Pi sayısının ne olduğunu anlamak kolaydır ancak rakamlarını hesaplamak oldukça zordur. 1/7 gibi bir sayının yazılması için sonsuz sayıda ondalık basamak gerekir – 0,1428571428571… – ancak sayılar her altı basamakta bir tekrarlanır, bu da sayının anlaşılmasını kolaylaştırır. Öte yandan Pi, tekrarlanan kalıpların olmadığı irrasyonel bir sayının örneğidir. Yani, bir kesir (iki tam sayının oranı) olarak ifade edilemez.
Pi irrasyonel olmasının yanı sıra aşkındır, yani tam sayıları içeren herhangi bir basit denklemle tanımlanamaz. Pi için bir formül arayışı, sayıya ilişkin matematiksel anlayışımıza katkıda bulunur. Aynı zamanda Pi sayısının tüm basamaklarını hesaplamak için genel bir formül geliştirmeyi başaran matematikçi muhtemel tarih boyunca anımsanacaktır.

Rekor kırmak pi’nin yeni rakamlarını bulmanın motivasyonlarından biri olsa da bunun iki önemli faydası vardır. Birincisi, süper bilgisayarların ve yeni yüksek hassasiyetli çarpma algoritmalarının geliştirilmesi ve test edilmesidir. İkincisi de pi’nin doğasının anlaşılmasıdır.
Ayrıca yüzyıllarca süren araştırmalara rağmen, rakamların nasıl davrandığına dair hala cevaplanmamış temel sorular mevcuttur. Örneğin pi sayısının ondalık açılımında bazı kalıplar var mı? Her rakam eşit sıklıkla mı karşımıza çıkıyor? Matematikçilerin peşinde olduğu sorular bu ve buna benzerdir.
Pi Sayısı Nasıl Hesaplanır?
3.000 ila 4.000 yıl önce matematikçiler, pi sayısını deneme yanılma yaklaşımları ile hesaplamaya çalışıyorlardı. Bu tip yöntemler ile Pi sayısı Babil’de (MÖ 1900-1600) 3,125 ve eski Mısır’da (MÖ 1650) 3,1605 olarak hesaplanmıştı. Gerçek değerden uzak olsa da yine de dönemin koşullarına göre oldukça doğru hesaplamalardı.
Ancak Pi’nin gerçek değerini bulmaya yönelik ilk titiz yaklaşım geometrik olacaktı ve arka plandaki isim ise adını kaldıraçlar, makaralar, gemi parçalayan düzenekler ile anımsadığımız Arşimet’ti (MÖ 287-212).
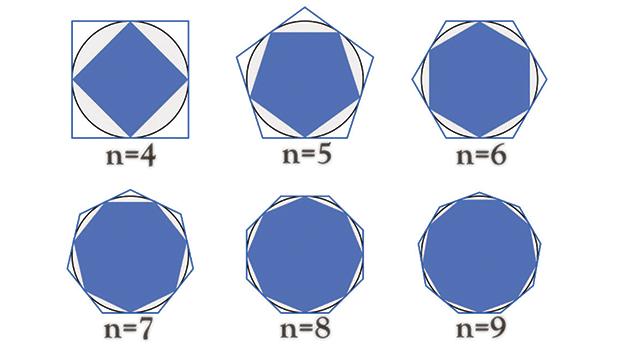
Arşimet, çemberlerin hem dış tarafına hem de iç kısmına çokgenler çizdi. Bunların çevrelerinin hesaplanması Pi sayısı için bir üst ve alt sınır verdi. Kendisi işe altıgenlerle başladı; Giderek daha fazla kenarı olan çokgenleri kullanarak sonuçta pi sayısının 223/71’den daha büyük ancak 22/7’den daha küçük olması gerektiğini söyledi. Gerçekten de günümüzde hesapladığımız pi değeri bu iki kesir arasında bir yerlerde bulunmaktadır.
Dünyanın dört bir yanındaki matematikçiler Arşimet’ten sonra Pi sayısını hesaplamaya devam etse de bunu yapma teknikleri 17. yüzyıldan sonra kalkülüs ve sonsuz seri tekniklerinin gelişmesiyle çarpıcı biçimde değişti. Örneğin, Madhava serisi (adını Hint matematikçi Sangamagrama’lı Madhava’dan almıştır ) şöyle diyor: π = (4/1) – (4/3) + (4/5) – (4/7) + (4/9) – (4/11) + (4/13) – (4/15)…Giderek daha fazla terim eklerseniz, bu hesaplama pi’nin gerçek değerine giderek daha da yaklaşacaktır.
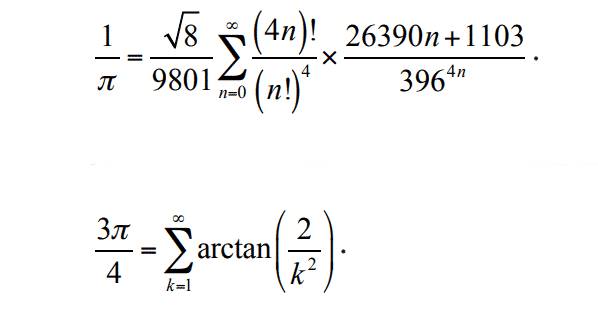
Ancak bu oldukça uzun bir zaman alır. Ramanujan da pi sayısının yaklaşık değerlerini hesaplamak için de yüzlerce formül geliştirmişti. Örneğin yukarıdaki ilk formülün her terimi, pi sayısının 8 yeni basamağını hesaplamamızı sağlar. Bu sayede 1985 yılında pi sayısının 17 milyon basamağını hesaplamak mümkün oldu. Günümüzde Pi sayısının basamaklarını hesaplamak için binlerce formül vardır. Ancak hızlı ve kesin bir formüle henüz ulaşılamamıştır.
Pi Sayısını Nasıl Ezberleriz?
Şu anki Pi sayısı ezberleme rekoru, 2005 yılında 67 890 basamak ezberlemeyi başaran Çinli Lu Chao’ya aittir. Kendisi bu basamakları 24 saat 4 dakika saymayı başarmıştır. Mantıksız gibi gelse de aslında pek çok kişi Pi sayısını ezberlemeye çalışır ve bunun içinde onlarca teknik vardır.
Tıpkı fiziksel egzersizin vücudunuz için iyi olduğu gibi, zihinsel antrenman da beyniniz için iyidir. Uzun süreli hafızayı eğitmek için π sayısının standart bir araç olarak kullanılmasının nedeni budur. Pi sayısı ezberleyicileri genellikle loci yöntemi olarak bilinen bir strateji de kullanırlar. Sonucunda zihnimizde oluşturacağımız hikayeler ile bilgiyi ilişkilendirirsek, bilginin hatırlanması o kadar kolay olur.
Pi Sayısını Evinizde Kolaylıkla Hesaplayabilirsiniz
Matematikçiler günümüzde pi sayısını hesaplamak için sonsuz serileri kullanırlar. Ancak Pi’nin değerini tahmin etmenin eğlenceli ve basit yöntemleri de vardır. Bunlardan en bilinenlerinden biri “Monte Carlo” adı verilen yöntemdir. Yöntem oldukça basittir. Evde denemek için aşağıdaki görselde gördüğünüz gibi bir kare ve karenin kenarlarına teğet bir iç çember çiziniz.
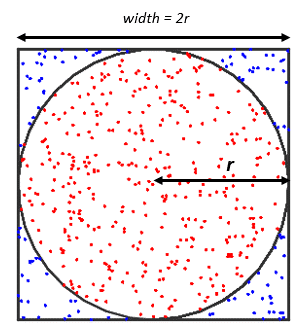
Karenin kenarlarının uzunluğunun 2 olduğunu, dolayısıyla alanının 4 olduğunu düşünün; dolayısıyla dairenin çapı 2, alanı ise pi’dir. Alanları arasındaki oran pi/4 veya yaklaşık 0,7854’tür. Şimdi bir kalem alın, gözlerinizi kapatın ve karenin üzerine rastgele noktalar koyun. Bunu yeterli sayıda yaparsanız ve çabalarınız gerçekten rastgeleyse, sonunda noktanızın dairenin içine düşme yüzdesi %78,54’e veya 0,7854’e yaklaşacaktır. Artık çağlar boyunca pi’yi hesaplayan matematikçiler arasına katıldınız.
Pi sayısı ile ilgili daha fazla şey görmek isterseniz yukarıdaki videoya göz atabilirsiniz. Arka planda dinleyeceğiniz müzik ise pi sayısını 12 lik tabana uygulayan Jim Zamerski tarafından bestelenmiştir. İyi seyirler.
Kaynaklar ve ileri okumalar için.
- Why bother calculating pi to 62.8 trillion digits? It’s both useless and fascinating. Yayınlanma tarihi: 18 Ağustos 2021. Kaynak site: Conversation. Bağlantı: Why bother calculating pi to 62.8 trillion digits? It’s both useless and fascinating
- Pi, Anyone? The Secret to Memorizing Tens of Thousands of Digits. Yayınlanma tarihi: 13 Mart 2015; Bağlantı: https://www.livescience.com/
- A Supercomputer Just Calculated Pi to a Record-Breaking 62.8 Trillion Digits. So What?; yayınlanma tarihi: 10 Ağustos 2021; Bağlantı: https://www.popularmechanics.com/
- Happy International Pi Day. Here Are 11 Intriguing Facts about Pi; Yayınlanma tarihi: 14 Mart 2020; Bağlantı: https://interestingengineering.com
Matematiksel











Bu sayfanın linkini nasıl alacağım? Yetkili biri veya bilen bir kişi yardım edebilir mi?