Arşimet adını kaldıraçlar, makaralar, gemi parçalayan düzenekler ve Arşimet vidasını icat etmesi aracılığı ile duymuş olabilirsiniz. Ancak aslında kendisi çemberler ve küreler üzerine de çok kafa yormuştur. Bu konuda pek çok kitap (ya da o günkü haliyle parşömen tomarı) yazmıştı. İronik bir şekilde, pi sayısı ile ilgili ilk incelemelerden bazıları, daha sıfır sayısı bile keşfedilmeden önce, onun tarafından yapıldı.

Aslında Arşimet’e kadar bir dairenin çevresi ile alanı arasında kesin bir bağlantı yoktu. Bu konudaki ilk kayıt Arşimet’in Dairenin Ölçümü isimli kitabında yer alır. Bu önemli kitapta, π değerinin tarihsel gelişiminde rol oynayan daire ile ilgili üç önerme bulunmaktadır. Bu üç önermeyi her birinin biraz açıklamasıyla birlikte inceleyelim.
1. “Bir dairenin alanı, dik kenarları sırasıyla bu dairenin yarıçapı ve çevresine eşit olan, bir dik üçgene eşittir.”
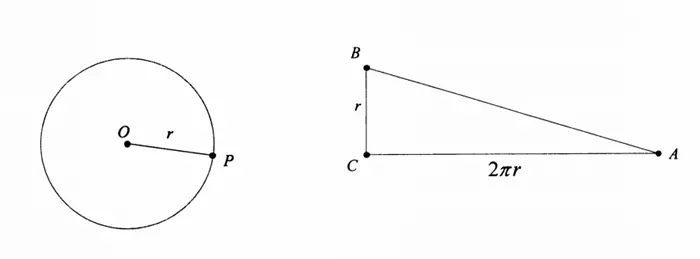
Aslında bu sözlerin günümüzde apaçık doğru olduğunu biliyoruz. Sonuçta bir dairenin alanı π. r2 kadardır. Ayrıca bahsedilen dik üçgenin alanı ise 1/2. r. 2πr yani sadeleştirmelerden sonra yine π. r2 olacaktır. Ancak Arşimet bunu biraz dolambaçlı bir şekilde ifade etse de, bugün kabul ettiğimiz formülü bu biçimde ifade etmesi etkileyicidir.
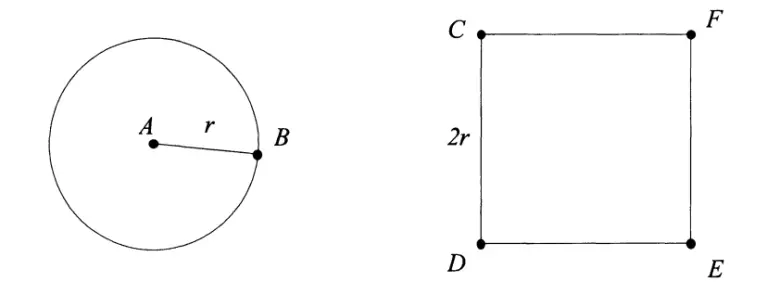
2. “Bir dairenin alanının, bir kenarı dairenin çapına eşit olan bir karenin alanına oranı 11:14’e yakındır.“
Bu önermeyi araştırmak için bize verilen oranı kurgulayalım. Dairenin alanı πr2‘dir ve bir kenarı 2r olan bir karenin alanı (2r)2 = 4r2‘dir. Bu iki alanı birbirine oranladığımız zaman sadeleştirmelerden sonra elimizde π/4 kalır. Arşimet bunun 11/14’e yakınsayacağını söylemişti. Bu nedenle ikisini birbirine eşitlersek π değeri 44/14 diğer bir deyişle 22/7 olacaktır.
3. “Herhangi bir dairenin çevresinin çapına oranı 22/7 ile 223/71 arasındadır.” Şimdi kendisinin bu fikri nasıl elde ettiğine biraz daha yakından bakalım.
Arşimet’in Yaklaşım Yöntemi
Arşimet, dairelerin yaklaşık değerlerini bulmak için çokgenleri kullanmayı denedi. İçine ve dışına birer çokgen çizerek dairenin çapının bu çokgenlerin çevrelerine oranlarını hesapladı. Dıştaki şeklin çevresi daireden daha büyük, içtekinin ise daha küçük olduğuna göre gerçek değer bu ikisinin arasında bir yerlerde olmalıydı. İşe öncelikle düzgün altıgen ile başladı.
Öncelikle çapı 1 birim olan bir daire çizdi. Sonrasında köşeleri bu daireye değen bir düzgün altıgeni içe, kenarları aynı daireye teğet olan, öncekinden biraz daha büyük, bir düzgün altıgeni dışa ekledi. Tanım gereği içteki dairenin çevresi pi sayısı kadar olacaktı. Bu çizim sayesinde daireyi bir alt ve üst sınır arasına yerleştirmiş oldu.
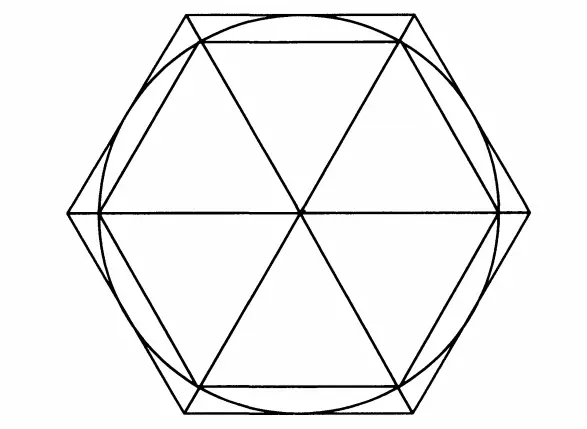
Arşimet, kenar sayısını artırdıkça şeklin daireye daha fazla yaklaşacağını biliyordu. Bu nedenle kenarları her seferinde ikiye bölerek kendine yeni sınırlar belirledi. Aynı çalışmayı 12 kenarlı, 24 kenarlı, 48 kenarlı ve en son olarak 96 kenarlı düzgün şekiller ile tekrarladı. Bu sayede her seferinde çemberin çevresine yani pi sayısına daha çok yaklaşıyordu.
Arşimet en sonunda pi sayısının 223/71’den daha büyük ancak 22/7’den daha küçük olması gerektiğini söyledi. Gerçekten de günümüzde hesapladığımız pi değeri bu iki kesir arasında bir yerlerde bulunmaktadır.
Arşimet’in Pi Sayısı Hesaplamasının Detaylarına Bir Göz Atalım
Onun düşündüğü bu yöntem gerçekten dahice idi. Sonuçta bir çokgenin kenar sayısı artıkça giderek çembere benzemeye başladığını hepimiz biliyoruz. Bunu aklınızda daha iyi canlandırmak için aşağıdaki 12 kenarlı düzgün çokgene göz atabilirsiniz.
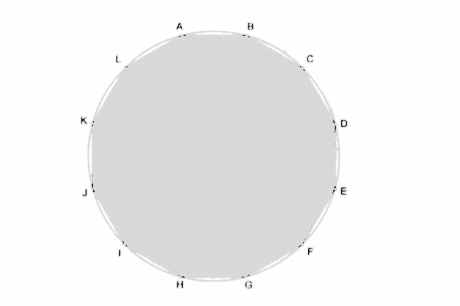
Ancak ufak bir sorunumuz var. Sonuçta yaşadığı dönemi göz önüne aldığımız zaman, Arşimet pi hesaplamalarını el ile yapmıştı. Çokgenimizin kenar sayısı arttıkça da bu hesaplamanın daha da zor olacağı aşikar. Peki bunu nasıl başarmıştı?
Cevap elbette trigonometri. İşleri basit tutalım ve altıgenimize geri dönelim. Dairenin çapı 1 birim idi. Düzgün altıgenin de altı tane eşkenar üçgenin birleşimi olduğunu biliyoruz. Görselde AOB açısının ölçüsü, 360° nin altıda biri yani 60° olmalıdır. Ayrıca OK doğru parçası AB kenarına diktir. Bu nedenle AK ve KB uzunlukları da birbirine eşittir. Buna a kadar diyelim. Ayrıca x ile gösterilen AOK açışı da 30 derecedir.
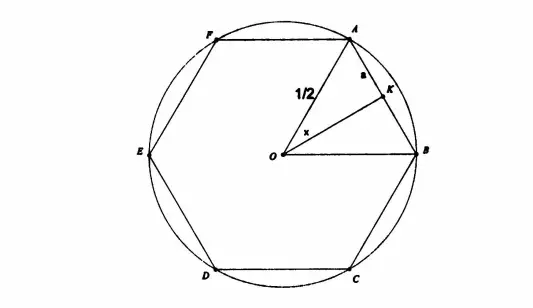
Altıgenimizin çevresini bulmaya çalıyoruz. Şimdi AOK üçgeninde trigonometri kullanalım. Bu durumda sin30= a/(1/2) =2a olacaktır. sin30=1/2 sonucunu bildiğimize göre 1/2=2a yani a=1/4 sonucunu elde ettik. Bu durumda altıgenimizin çevresi 12a olduğuna göre 3 olacaktır.
İşte şimdi bu elde ettiğimiz sonucu n kenarlı bir çokgen için genellememiz gerekiyor. Her durumda şeklimiz düzgün olduğu için aradığımız x açısının 360/n tepe açısının yarısı olduğunu biliyoruz. ( Burada n çokgenin kenar sayısını temsil ediyor).
Biraz önce aktardığımız mantıkla sin (180/n)= 2a olacaktır. Çokgenin çevresi n tane 2a kadar olmak zorundadır. Bunu n. sin (180/n) olarak da düşünebiliriz. Bundan sonra yapmamız gereken n sayısı yerine çeşitli değerler atamaktır. Aşağıda belli sayılar atadığımız zaman elde edilen sonuçları görebilirsiniz.
Çokgenin Çevresi İle Pi Sayısının İlişkisi

Şimdi yukarıdaki sayılar arasında son satıra dikkat edin. Buradaki rakamları zaten bildiğimiz pi sayısının rakamları ile karşılaştırın. ( π: 3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944…).
Gördüğünüz gibi virgülden sonraki altı basamak aynı. Aslında n yerine daha büyük sayılar koyarak pi sayısının diğer basamaklarını da bu biçimde bulabiliriz. Ancak Arşimet’in pi sayısı hesaplama çabaların da hesap makinesi olmadığını anımsayalım.
Dış Teğet Çokgen İle Pi Sayısına Yaklaşım
Şu ana kadar verdiğimiz açıklamalar bir çemberin içine çokgen çizilmesi ile ilgili idi. Şimdi de hızlıca bunun tam tersine bakalım. Bir çok süreç benzer olduğu için arada bazı kısımları atlayacağız. Bu sefer hesaplaması daha kolay olduğu için düzgün beşgen ile çalışalım.
Yapmamız gereken bir kenarı 2a olan düzgün bir çokgenin çevresini hesaplamak için bir yöntem geliştirmek. Aşağıdaki şekilde AOB açısının 72 derece olduğunu biliyoruz. Bu sefer bildiğimiz kenarları göz önünde bulundurarak tanjantı kullanalım. tan36=a/(1/2) =2a kadardır. Bu durumda a kenarımız yaklaşık 0.36327126400268044294773337874031 olacaktır. Çevre için bu sayıyı 10 ile çarpmamız lazım. Bunun sonucunda beşgenimizin çevresi yaklaşık 3.6327126400268044294773337874031 olur.
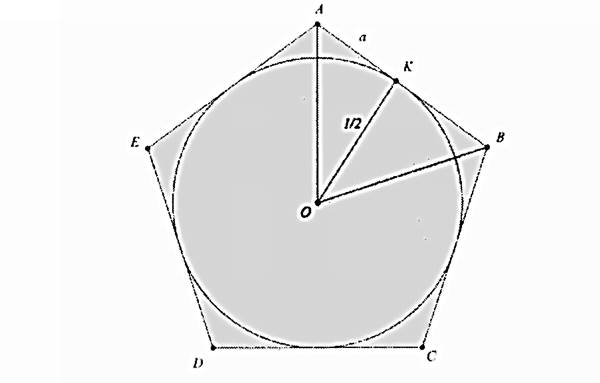
Son olarak genel bir kural bulalım. Bu da n kenarlı düzgün bir çokgen için n.tan (180/n) kadar olacak. Şimdi n yerine rakamlar vererek çokgen büyüdükçe ortaya çıkan çevrelere bakalım. Sonuçta n sayısının arttıkça dış teğet çokgenimizin çevresinin de giderek pi sayısına yaklaştığını görüyoruz.

Arşimet pi sayısını hesaplamak için bu kadar çok sayı deneyemezdi ancak şaşırtıcı bir öngörü ile doğru sonuca ulaşmıştı. Yöntemi o kadar sağlamdı ki sonraki beş yüz yıl boyunca kimse daha yakın bir sonuç elde edemedi.
Kaynaklar ve ileri okumalar
- The beautifully simple method Archimedes used to find the first digits of pi; Yayınlanma tarihi: 15 mart 2019; Bağlantı: https://www.businessinsider.com/
- King, Alessandra. (2013). Finding Pi with Archimedes’s Exhaustion Method. Mathematics Teaching in the Middle School. 19. 116-123. 10.5951/mathteacmiddscho.19.2.0116.
Matematiksel