Yazıyı okumadan önce elinize bir kağıt kalem alın. Şimdi kağıdınıza, canınızın istediği biçimde, bir üçgen çizin. Şimdi her açıyı üçe bölün. Açı ölçeriniz yok ise göz kararı da bölebilirsiniz. Sonucunda şekliniz yaklaşık olarak aşağıda gördüğünüz biçimi alacaktır. Merkezde de küçük bir üçgen oluşacaktır.
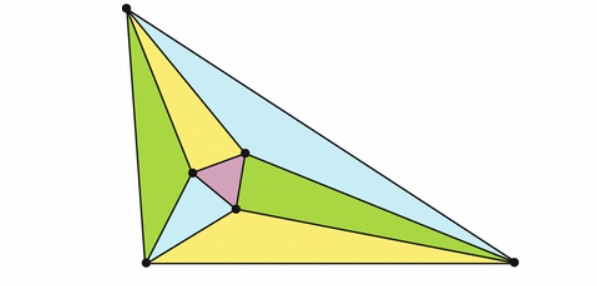
Elle düz çizgileri çizecek kadar yetenekli olduğunuzu varsayarsak, şaşırtıcı bir şey fark edeceksiniz: Hangi üçgenle başlarsanız başlayın, ortadaki küçük üçgen eşkenardır. Yani tüm kenarları aynı uzunluktadır. İşte bu Morley teoremidir ve ortada oluşan üçgene de Morley üçgeni adı verilmektedir.
1899 yılında İngiliz matematik profesörü Frank Morley geometride en çok şaşırtan ilişkilerden birini keşfetti. Bulduğu teorem o kadar yalın ve güzeldi ki dünya üzerinde ses getirmesi çok da uzun sürmedi. Öklid geometrisinde daha fazla keşfedilecek bir şey kalmadığını düşünenler için de bu teorem heyecan verici yeni bir gelişme idi.
Frank Morley Kimdi?
Frank Morley (1860–1937), 1900’den 1928’e kadar Johns Hopkins Üniversitesi’nde profesörlük yaptı. Aynı zamanda American Journal of Mathematics’in editörlük görevini sürdürdü. Bu esnada iki kitap yayınladı. Ayrıca Amerikalı okuyuculara 19. yüzyıl Avrupa matematik tarihinin önemli noktalarını tanıttı. En az 45 doktora öğrencisine sahip seçkin bir öğretmen olarak tanındı.

Bu bir profesör için oldukça büyük bir rakamdı. Aynı zamanda yetenekli bir satranç oyuncusuydu. Bir zamanlar dünya şampiyonu olan Emmanuel Lasker’ı satrançta yenmişti. Ancak Morley adı esas olarak 1899’da keşfettiği ancak 1929’a kadar yayınlamadığı bu teorem ile anımsanır.
Morley Teoremi Nedir?
Morley Teoremi özetle şunu söyler. Herhangi bir üçgenin üç parçaya bölünmüş komşu açısı üç noktada kesişmektedir. Bu kesim noktaları da bir eşkenar üçgen oluşturur. Teoremin güzel yanı üçgenin dar açılı, geniş açılı üçgen olmasından bağımsız bir şekilde her üçgene uygulanabilmesi. Ayrıca Morley teoremi sadece iç açılar için değil dış açılar için de geçerlidir.
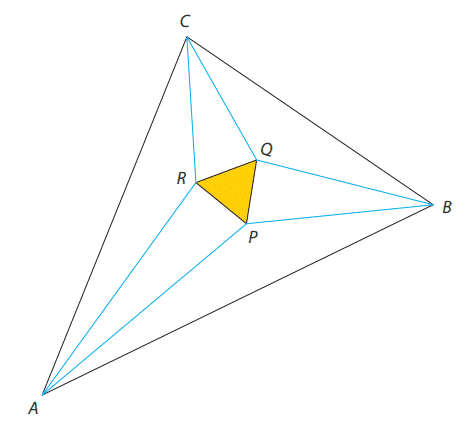
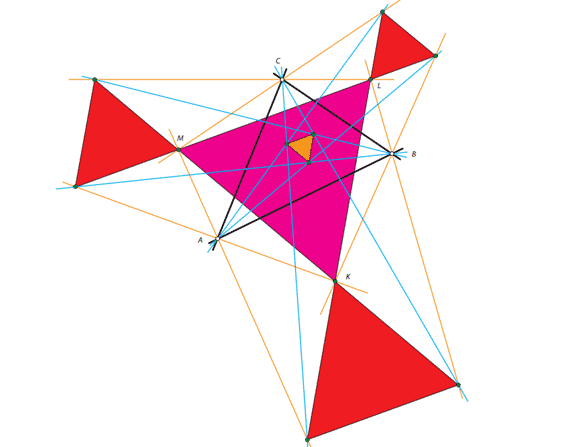
K, L ve M noktaları yine, şekilde mor ile gösterilen bir eşkenar üçgeni oluşturur. Ve hepsi bu kadar değil: kalan çizgilerin kesişimleri de yine eşkenar üçgenler yaratır. ( Şekilde kırmızıyla gösterilmiştir). Sonucunda, tüm eşkenar üçgenlerin tek bir genel üçgenden üretildiği düşünüldüğünde, bu sonuçlar gerçekten dikkate değerdir.
Morley Teoremi Neden Dikkat Çekti?
Öklid bir üçgende herhangi bir iki iç açının açıortaylarının üç kenara eşit uzaklıkta bir noktada buluştuğunu göstermişti. Bu noktayı hepimiz iç teğet çemberin merkezi olarak biliyoruz. Bu noktada da akla gelen bir soru vardır. Bu da bir üçgenin, üç eşit parçaya bölünmüş iç açılarının nasıl buluşacağı ile ilgilidir. Bu sorunun cevabı yaklaşık 2000 yıl sonra Morley teoremi sayesinde verilmiştir.
Sorunun çözümü için bu kadar zaman geçmesinin en önemli nedeni de antik çağdan günümüze taşınan bir sorundur. Bu sorun sadece işaretli olmayan bir cetvel ve pergel kullanarak verilen bir açıyı üç eşit parçaya bölmeyi nasıl yapacağımızı bilmemek ile ilgilidir. Sonuçta matematikçilerin ilk olarak bu sorunun üstesinden gelmesi gerekmiştir.
Bu teoremin bir çok farklı ispatı bulunmaktadır. İspatların çoğu uzun ve karmaşık olduğu için detaylarına yazımızda değinmeyeceğiz. Ancak ilgi duyanlar bu ispatları kaynaklar bölümümüzde bulabilirler. Ayrıca bu yazımıza da göz atmak isteyebilirsiniz: Bilim İnsanlarının Seçtiği En Güzel 10 Denklem
Kaynaklar ve ileri okumalar için:
- Morley’s trisector theorem; Bağlantı: https://en.wikipedia.org/
- Morley’s theorem; https://personal.math.ubc.ca/
- Eli Maor and Eugen Jost; Beautiful geometry; Princeton University Press; 2014
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






