Matematikçiler için denklemler birer sanat eseridir. Ancak, tıpkı sanatsal güzellikte olduğu gibi, matematiksel güzellik de bakan kişinin gözündedir. Bir matematikçi, basit ve özlü ifadeleri tercih edebilirken, bir diğeri bunun tam tersini beğenebilir. Yazının devamında farklı matematikçilerin seçtikleri en güzel denklemlere göz atalım.
Gauss-Bonnet Denklemi
—Ailana Fraser, British Columbia Üniversitesi
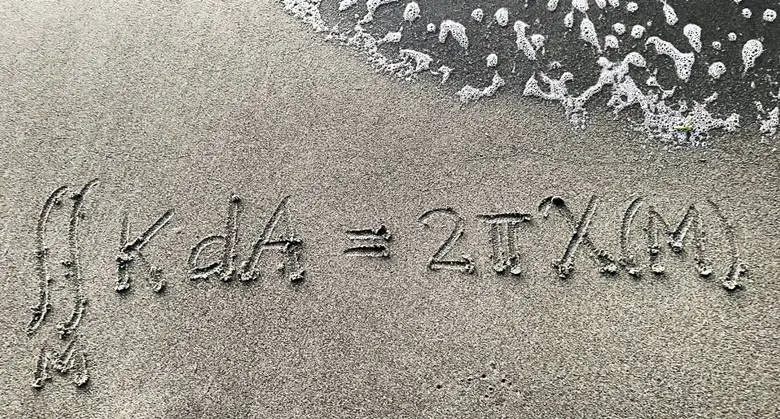
Bazı denklemler güzeldir, çünkü farklı özneler arasındaki beklenmedik ilişkileri ortaya çıkarırlar. Buna bir örnek, Gauss-Bonnet formülüdür. Bu denklem, diferansiyel geometri ve topolojide temel bir teoremi ifade eden matematiksel bir ilişkidir. Bir yüzeyin geometrik özelliklerini (eğrilik) topolojik özellikleri (örneğin, delik sayısı gibi) ile ilişkilendirir.
İlk olarak Carl Friedrich Gauss ve Pierre Ossian Bonnet tarafından ortaya konulan bu teorem, yüzey geometrisi ile topolojik değişmezler arasında köprü kurar. Yüzey eğriliği analizine dayanan modellerde, örneğin elastik yüzeyler veya kabuk yapılarının davranışını anlamak için kullanılır. Bu denklemin güzel yönlerinden bazıları, ifadesinin sadeliği ve söylediklerinin derinliğidir.
Sobolev Eşitsizliği
— Karen Uhlenbeck, Institute for Advanced Study
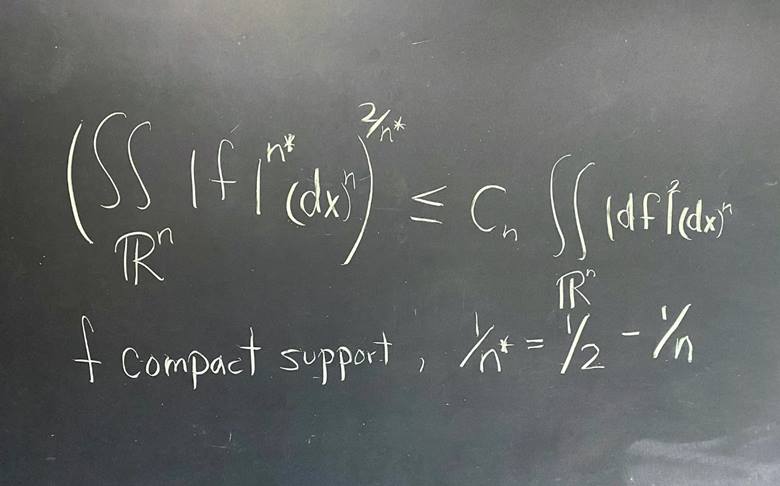
Sobolev eşitsizliği, bir fonksiyonun türevlerinin davranışını, fonksiyonun kendisinin büyüklüğü veya genel davranışıyla ilişkilendiren matematiksel bir bağıntıdır. Bu eşitsizlik, matematikte, özellikle kısmi diferansiyel denklemler, fonksiyonel analiz ve geometri alanlarında yaygın olarak kullanılır.
Yukarıdaki eşitsizliği anlamak için basit bir örnek verebiliriz. Bozuk bir yolu düşünün (Burada yol, fonksiyonu temsil eder). Yolun genel şekli (büyüklüğü veya davranışı), ne kadar virajlı ve engebeli olduğuna (türevlerine) bağlıdır. Eğer tümsekler (türevler) çok büyük değilse, yolun kendisi nispeten düzgün bir durumda kalır. Sobolev eşitsizliği, bu fikri matematiksel olarak ifade eder.
Loewner Diferansiyel Denklemi
— Ewain Gwynne, Chicago Üniversitesi
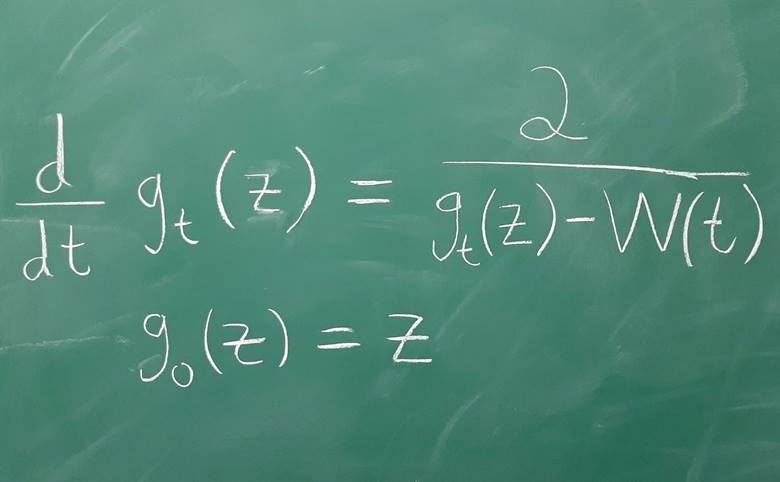
Loewner Diferansiyel Denklemi, matematikte konformal haritalama (açıyı koruyan dönüşümler) teorisinde kullanılan önemli bir araçtır. İlk olarak 1923 yılında Charles Loewner tarafından tanıtılmıştır. Bu denklem, bir bölgeyi zaman içinde değiştirerek başka bir bölgeye haritalayan bir süreci tanımlar.
Loewner diferansiyel denklemi, bir şeklin (örneğin, bir alanın veya bir düzlemin alt kümesinin) zamanla nasıl değiştiğini tanımlar ve bu değişimi, sürücü fonksiyonu adı verilen bir fonksiyon kontrol eder. (Bu sürücü fonksiyon, denklemin “yöneticisi” gibidir.)
1999 yılında Oded Schramm, Loewner diferansiyel denkleminin, sürücü fonksiyon olarak Brown hareketi (rastgele bir süreç) seçildiğinde özel bir simetriye sahip olduğunu keşfetti. Bu keşif, istatistiksel mekaniğin matematiksel çalışmasında devrim yarattı ve son yirmi yılda matematikteki en heyecan verici atılımlardan bazılarını ortaya çıkardı.
Riemann-Roch Eşitliği
—Sándor Kovács, Washington Üniversitesi
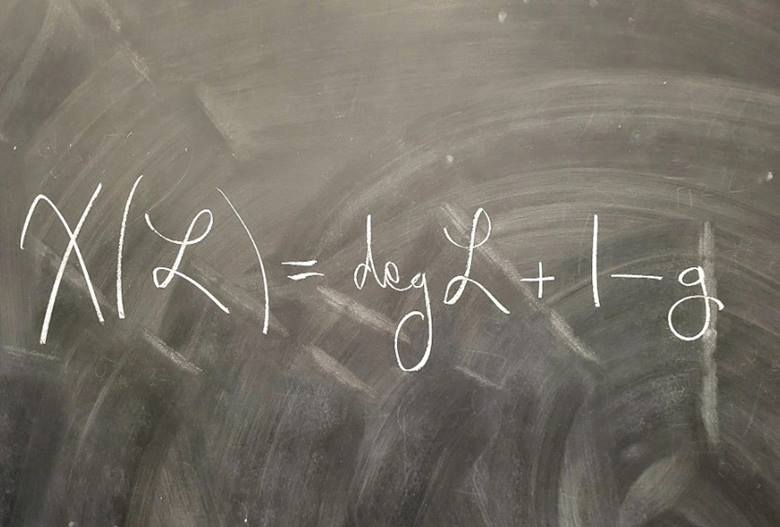
Bir denklemi güzel yapan şeyin ne olduğu kişiden kişiye değişir ancak bazı matematikçiler için görünüşte alakasız şeyleri birbirine bağlayan denklemler, en güzelleridir. Buna bir örnek Riemann-Roch Eşitliğidir.
Riemann-Roch Eşitliği, cebirsel geometri ve karmaşık analizde önemli bir kavramdır. Basitçe anlatmak gerekirse, bu eşitlik bir cebirsel eğrinin üzerinde tanımlı olan çizgisel demetlerin özelliklerini hesaplamaya yardımcı olur.
Cebirsel eğrilerin analizi için temel bir araçtır ve holomorfik fonksiyonların özelliklerini eğrinin geometrik yapısıyla birleştirir. ( Bir fonksiyonun holomorfik olması, onun belli bir bölgede çok düzenli ve düzgün bir yapıya sahip olduğunu ifade eder.)
Euler Çarpım Formülü
— Richard Schwartz, Brown Üniversitesi
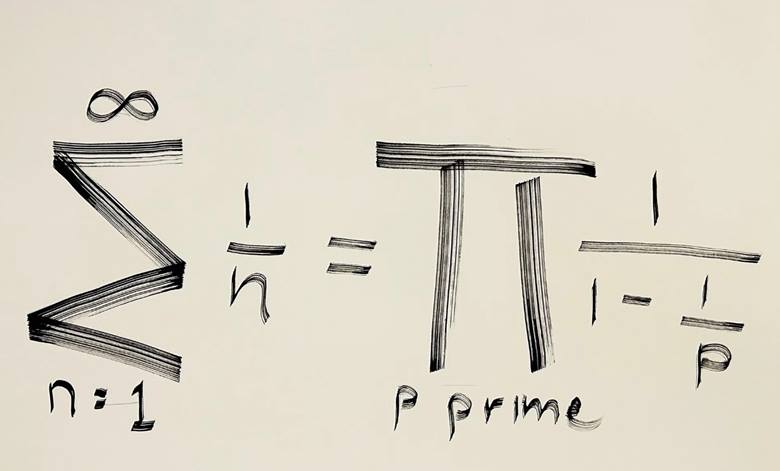
Matematikte en güzel denklemi seçmek zordur, ancak kimi matematikçilere göre Euler çarpım formülünün bu tür herhangi bir listenin en başında olması gerekir.
173t’te Leonhard Euler tarafından bulunan bu formül, sonsuz bir toplam ile sonsuz bir çarpım arasındaki bir ilişkiyi gösterir. Euler çarpımı, pozitif tam sayıları asal sayılar üzerinden ifade etmenin bir yoludur. Asal sayıların pozitif tam sayıların temel yapı taşları olduğu fikrini matematiksel olarak gösterir. Bu bağlantıyı zeta fonksiyonu üzerinden formüle eder.
Euler’in makalesinden yüz yirmi yıl sonra, Bernhard Riemann asal sayılar üzerine ünlü 1859 tarihli makalesini yayınlamıştı. Bernhard Riemann, zeta fonksiyonunu karmaşık analiz düzlemine genişletmiş ve Riemann Hipotezi gibi büyük problemleri formüle etmişti.
Euler’in çarpım formülü onun bu makalesinin merkezinde yer alıyordu. Euler Çarpımı, bugün analitik sayı teorisinin temel araçlarından biridir ve asal sayıların dağılımını incelemek için kullanılmaktadır.
Minimal Yüzey Denklemi
— Frank Morgan, Williams College
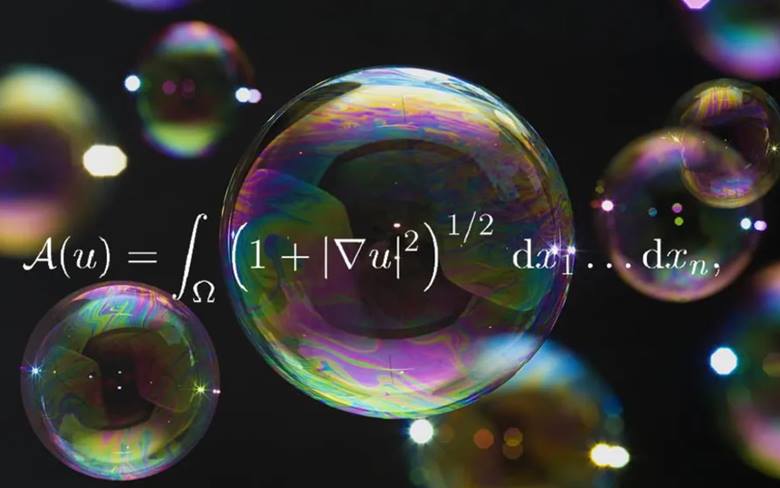
fonksiyonunu bulmayı amaçlar.
Minimal yüzeyler, genellikle bir sınır koşuluyla en küçük alanı kaplayan yüzeylerdir ve genellikle fiziksel bir sistemdeki dengede olan ince bir zarın veya bir sıvı film tabakasının matematiksel modelini temsil eder. Bir yüzey, eğriliği tanımlayan ortalama eğrilik her noktada sıfırsa, minimal yüzey olarak adlandırılır.
Örneğin, bir çerçevenin içine yerleştirilmiş sabun filmi minimal yüzey oluşturur, çünkü yüzey enerjisini minimize etmeye çalışır. Minimal yüzeyler, diferansiyel geometri ve geometrik analizde temel bir çalışma konusudur.
Çok Yüzlüler için Euler Formülü
— Colin Adams, Williams College
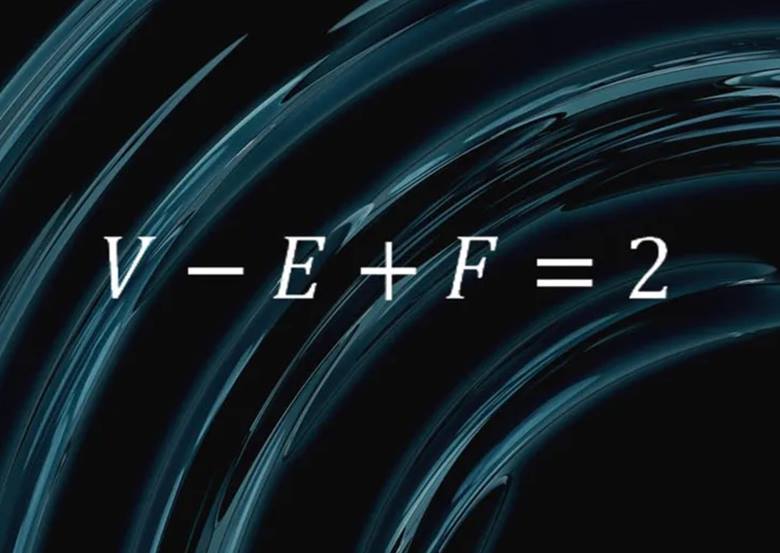
Bu formül, düzgün çokyüzlülerin temel özelliklerini açıklar. “V” köşe sayısını, “E” kenar sayısını, “F” ise yüz sayısını ifade eder. Denkleme göre, yüz sayısı ile köşe sayısının toplamından kenar sayısını çıkarırsanız, daima 2 elde edersiniz.
Bu formül, 18. yüzyılda matematikçi Leonhard Euler tarafından geliştirilmiştir. Euler, bu formülü konveks çokyüzlülerin geometrik özelliklerini analiz etmek için kullanmıştır. Zamanla da formül topolojinin temel taşlarından biri haline gelmiştir.
- Küp için: Köşe sayısı (V): 8, Kenar sayısı (E): 12, Yüz sayısı (F): 6 ise V−E+F=8−12+6=2
- Dört Yüzlü (Tetrahedron) için: Köşe sayısı (V): 4, Kenar sayısı (E): 6, Yüz sayısı (F): 4 ise V−E+F=4−6+4=2 sonucunu elde ederiz ve bu biçimde devam edebiliriz.
Euler Formülü topoloji açısından temel öneme sahiptir. Euler’in gözlemi şimdi topolojik değişmez olarak adlandırılanların ilk örneklerinden biriydi. Euler formülü sadece konveks çokyüzlüler için değil, aynı zamanda daha karmaşık yüzeyler ve şekiller için de genelleştirilebilir.
Örneğin, bir yüzeyin Euler karakteristiği (χ) şu şekilde ifade edilecektir. Bu karakteristik, bir şeklin geometrik veya topolojik özelliklerini belirlemeye yardımcı olur. Örneğin küre için χ=2 iken, torus için χ=0 olacaktır.
Sizin için en güzel denklem hangisi? Bunu yorumlara ekleyebilirsiniz. Ayrıca bu yazımıza da bakabilirsiniz: Dünyayı Değiştiren Günümüzü Biçimlendiren 17 Denklem
Kaynaklar ve ileri okumalar:
- Clara Moskowitz; The 11 Most Beautiful Mathematical Equations. Yayınlanma Tarihi: 1 Temmuz 2017; Yayınlandığı Yer: Livescience; Bağlantı: The 11 Most Beautiful Mathematical Equations/
- These Are the Most Beautiful Equations, according to Mathematicians. Yayınlanma tarihi: 20 Haziran 2024. Kaynak site: Scientific American. Bağlantı: These Are the Most Beautiful Equations, according to Mathematicians
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






e*iπ
+1=0