Matematik ve biyoloji yan yana düşünülmesi zor olan iki kavramdır. Ama gel gör ki dağ dağa kavuşamasa da, iki zıt bilim birbirine kavuşur. Bu kavuşma günümüzde biyomatematik ya da matematiksel biyoloji adı ile bilinmektedir.

Biyoloji aslında deneysel bir bilimdir, yani hipotezlerini doğrulamak için deneye ihtiyaç duyar. Ama biyoloji sadece deneyden ibaret de değildir. Deneyle ilgilenen kısma “Deneysel Biyoloji”, teorilerle ve bizim de konumuz olan matematiksel biyolojiyle ilgilenen kısma da “Kuramsal / Teorik Biyoloji” denir. Matematiksel biyoloji, mikrobiyoloji, biyoteknoloji, evrimsel biyoloji ve sağlık hizmetlerinde devrim yaratmayı vaat eden, büyüyen bir alandır.
Bu matematik ile arası pek de iyi olmadığı için tercihini biyolojiden yana kullananlar için kötü haber olacaktır. Ancak matematik artık biyolojide hayati bir rol oynamaktadır. Bunun sonucunda da öğrencilerin matematiksel becerilere ihtiyacı vardır.
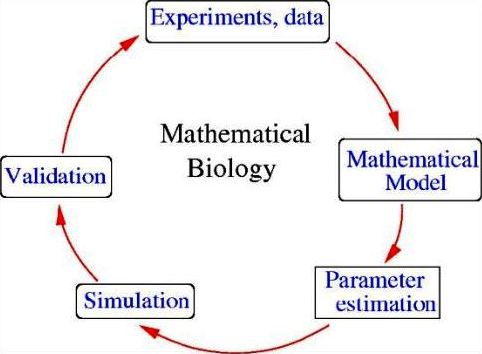
Matematiksel Biyoloji ya da Biyomatematik Nedir?
Biyomatematik, aslında matematiksel modellemeler, soyutlamalar ve teknik analizlerin yapıldığı “Uygulamalı Matematik”in bir alt dalıdır. Biyomatematik, deneysel biyolojinin yetersiz kaldığı ya da saha çalışmalarının imkansız olduğu durumlarda imdada yetişir.
Biyolojinin dinamik süreçlerini sayısal modellere “çevirir”, böylece diğerlerinin yanı sıra zoologlar, fizikçiler, virologlar ve istatistikçiler için ortak bir öğrenme alanı yaratır. Bu sayede de biyolojik bir süreçle ilgili bilgi elde etmek için, o sürecin olup bitmesini beklemek zorunda kalmayız.
Bir zamanlar biyoloji, zooloji ve botanik, hayvanlar ve bitkilerin incelenmesi anlamına geliyordu. Mikroskobun icadı, vurguyu hücre düzeyine kaydırdı ve son zamanlarda odak moleküler düzey halini aldı. Matematik, biyoloji tarihinde ilk defa 1760 yılında çiçek hastalığının matematiksel analizinde kullanıldı. Takip eden yıllarda da daha pek çok salgın hastalığın modellemesi çeşitli matematikçiler tarafından yapılacaktı.

Sonunda 1923 yılında Dr. William Moses Feldman (1880-1939) tarafından, “biyomatematik” terimi icat edildi. Kendisi bu kelimeyi bir makalesinin başlığında kullanmıştı ve muhtemelen pek de önemli olduğunu düşünmemişti. Ancak onun ortaya attığı bu kavram yaklaşık 100 yıl sonra biyoenformatik, biyoistatistik veya hesaplamalı biyoloji gibi güncel gelişmelerle son derece ilgili disiplinler için kullanılacak bir ifade olacaktı.
Ukraynalı teorik fizikçi Nicolas Rashevsky (1899-1972), matematiksel biyoloji üzerine ilk bilimsel makale olarak kabul edilen makaleyi 14 yıl sonra yayınladı. Bir yıl sonra da konu ile ilgili bir dergi çıkartmaya başladı. Bu nedenle kendisi matematiksel biyolojinin babası olarak kabul edilir. Ancak gerçek şu ki söylemlerinin biyologlar camiasını etkilemesi için aradan biraz daha zaman geçmesi gerekmiştir.

Matematiksel Biyoloji Nerede Kullanılmaktadır?
Biyolojik sistemler özünde son derece karmaşıktır. Ancak basit matematiksel modeller sayesinde bu sistemdeki temel unsurları ve süreçleri izole etme ve açıklama şansımız olacaktır. Aslına bakarsanız, biyolojideki birçok problem, ağ analizi, grup teorisi, diferansiyel denklemler, olasılık, kaos teorisi ve kombinatorik gibi diğer alanlarda geliştirilen matematiksel teknikler kullanılarak çözülmüştür.

Örneğin matematiksel biyoloji sayesinde, bir DNA molekülünün birleşimi düğüm teorisi kullanılarak incelenmektedir. Grup teorisi, hayvanların yürüme şekli gibi bir şeyi açıklamak için kullanılmaktadır. Biyomatematik ayrıca kan damarlarındaki, bitkilerin yapraklarındaki veya akciğerlerimizin bileşenlerin fraktal biçimindeki yapılarını da incelemekte kullanılmaktadır.
Bir proteinin şekli, işlevlerini belirlemede önemli bir faktördür. Protein moleküllerinin katlanması ve birbirine dolanması ise yine düğüm teorisi kullanılarak modellenmektedir. Biyomatematiğin bir diğer büyük ismi de diğer birçok bilimsel başarılarıyla ünlü olan Alan Turing’dir. Kendisi her organizmanın belirli şekillerini (morfogenez) oluşturan süreçlerle ilgileniyordu.

Kendisi sonunda bir örüntü oluşumu için reaksiyon-difüzyon teorisi adı verilen bir teori geliştirdi. 1952’deki bu teori, nesneler veya organizmalar içindeki kimyasalların yayılıp sonra birlikte reaksiyona girdiğinde doğadaki tanınabilir desenlerin kendiliğinden ortaya çıkabileceğini öngördü. Günümüzde Turing denklemleri biyoloji ve robotikten astrofiziğe kadar çeşitli alanlarda karşımıza çıkıyor. Bu nedenle Turing, “çağdaş Matematiksel Biyolojinin kurucusu” olarak kabul ediliyor.
İnsan Sağlığı Ve Matematik
Matematik aynı zamanda COVİD-19 ile mücadelemizde de ön saflarda yer aldı. Haberleri izlediyseniz muhtemelen bir salgının meydana gelip gelmeyeceğini belirten matematiksel bir kavram olan R0’ı duymuşsunuzdur.
R0 1’den büyük olduğunda enfeksiyon sayısı artar. R0’ın 1’den küçük olması durumunda salgın eninde sonunda yok olacaktır. Bulaşıcı hastalık epidemiyolojisindeki bu önemli kavram, matematik ve istatistiğin, verilerdeki başka türlü fark edilemeyecek kadar ince kalıpları tespit etme gücünün bir sonucudur.
Artık biyolojide yeni bir çağın başlangıcındayız. Bir hücreyi kapsamlı bir şekilde tanımlamak için matematiksel modeller oluşturabiliyoruz. Bu sayede bir hücrenin ömrünü hesaplayabiliyor ve insan vücudunun nasıl çalıştığını anlayabiliyoruz. Tüm bunlar matematiksel biyoloji alanında yapılan çalışmaların bir sonucudur.
Sonuç Olarak
Matematiksel modeller işlevi henüz bilinmeyen genlerin rolünü belirlemeye, viral enfeksiyonlara yönelik strateji ve tedavileri optimize etmeye veya gelecekteki nörolojik bozuklukların erken teşhisini sağlamaya hizmet edebileceğinden, matematik kişiselleştirilmiş ve öngörücü tıbbın anahtarını elinde tutuyor. Matematik ve biyolojinin bu birleşimi, yaşamın varlığını belirleyen sırları sayısal kodlarla çözmemizi sağlayacak gibi gözüküyor.
Kaynaklar ve ileri okumalar
- Biomathematics: the numerical secrets of biology. Yayınlanma tarihi: 17 Haziran 2020. Kaynak site: BBVA Open Mind. Bağlantı: Biomathematics: the numerical secrets of biology
- Cass, J.F., Bloomfield-Gadêlha, H. The reaction-diffusion basis of animated patterns in eukaryotic flagella. Nat Commun 14, 5638 (2023). https://doi.org/10.1038/s41467-023-40338-2
- Biomathematics: the New Frontier, yayınlanma tarihi: 21 Ağustos 2014; Bağlantı: Biomathematics: the New Frontier/
- The next breakthrough tool in biology? It’s maths. Here are some ways mathematical biology is helping change the world. Kaynak site: Conversation. Yayınlanma tarihi: 10 Temmuz 2022. Bağlantı: The next breakthrough tool in biology? It’s maths. Here are some ways mathematical biology is helping change the world
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel