Bir çoğumuz iki nokta arasındaki en kısa mesafenin düz bir çizgi olduğunu düşünürüz. Ancak bu söz yalnızca kısmen doğrudur çünkü iki nokta arasındaki en kısa mesafe nesnenin şekline bağlıdır. Bu fikir bizi jeodezik eğri kavramına götürür ve uçakların neden düz değil de eğri bir rota üzerinde seyahat ettiklerini açıklar.
Zamanın başlangıcından beri insanlık A noktasından B noktasına gitmenin daha hızlı yollarını aradı. Bunun için giderek daha hızlı hale gelen çeşitli taşıtlar icat etti. Ancak seyahatte dikkate alınan tek şey hız değildir. Hızın yanında seçilen rotanın en kısa olduğundan emin olmak da önemlidir.
Düz bir Dünya üzerinde olsaydık (ki elbette değiliz), o zaman iki nokta arasındaki en kısa yol düz bir çizgi olurdu. Ancak dünyamız düz değil küreseldir. Bu nedenle de yüzeyinde çizeceğiniz bir çizgi düz değil eğri biçiminde olacaktır. O zaman iki nokta arasındaki en kısa mesafeden bahsettiğimiz zaman bir değil birden fazla çizgiyi göz önüne almalıyız. Bu durumda bir genelleme yapmamız gerekir.
Jeodezik Eğri Nedir?
Aşağıdaki görseli Dünya olarak kabul edelim. Şimdi bir yürüyüşe çıkalım. Ekvatordaki bir noktadan başlayın ve kuzey kutbuna kadar bir boylam çizgisini takip edin. Bu çizgi her zaman ekvator ile 90 derecelik bir açı oluşturur.
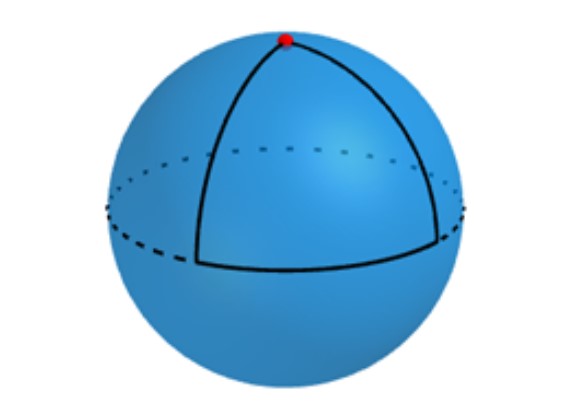
Sonrasında az önce yürüdüğünüz boylamla 90 derecelik bir açı yapan başka bir boylam çizgisi bulun. Bu yeni boylam çizgisi boyunca tekrar ekvatora ulaşana kadar yürüyün. Şimdi de başlangıç noktanıza ulaşana kadar ekvator boyunca yürüyün. Üzerinde yürüdüğünüz çizgiler, küre üzerinde büyük dairelerin, yani kürenin kendisiyle aynı çapa sahip dairelerin parçalarını oluşturur. Her çizgi büyük bir dairenin çeyreğine denk gelir. Bu nedenle hepsinin uzunluğu aynıdır.
Bir küre üzerindeki büyük daireler, düzlemdeki düz çizgilerin benzerleridir. Bunun sonucunda da bir düzlemdeki iki nokta arasındaki en kısa mesafenin düz bir çizgi üzerinde olması gibi, bir küre üzerindeki iki nokta arasındaki en kısa mesafe de büyük bir daire boyunca olacaktır.
Bir yüzey üzerinde yer alan ve iki nokta arasındaki en kısa mesafeyi belirten eğriye jeodezik eğri denir. Söz konusu yüzey bir düzlem ise iki nokta arasındaki en kısa mesafeyi veren düz çizgiler bir düzlemin jeodezikleridir. Bir kürede ise jeodezik, az önce de dediğimiz gibi büyük dairelerin bölümleridir.
Bir düzlemde, herhangi iki nokta arasında her zaman yalnızca bir jeodezik vardır. Bir küre üzerinde ise sonsuz sayıda jeodezik bulunur. Geometride jeodezik eğriler oldukça kapsamlı araştırma konularından biridir. Bu yazıda biz daha çok küresel geometriye odaklanacağız. Biraz daha detay için bu yazıya da göz atabilirsiniz: Kare Nedir? Cevap Gauss Eğriliğine Göre Değişir!
Uçaklar düz gitmek yerine neden eğik bir rotada giderler?
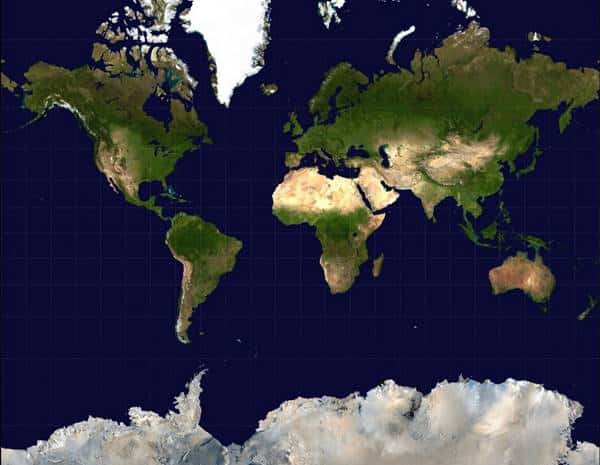
Uçak rotaları düz bir çizginin en kısa mesafe gibi görünebileceği 2 boyutlu bir haritada belirtilmiştir. Ancak, Dünya’nın hiçbir 2 boyutlu haritası aslında gerçek biçimde çizilmemiştir. Çünkü bir küreyi dikdörtgen bir şekle dönüştürmeye çalıştığımızda, çoğu haritada gözlemlenen şekilde bozulmalar meydana gelir.
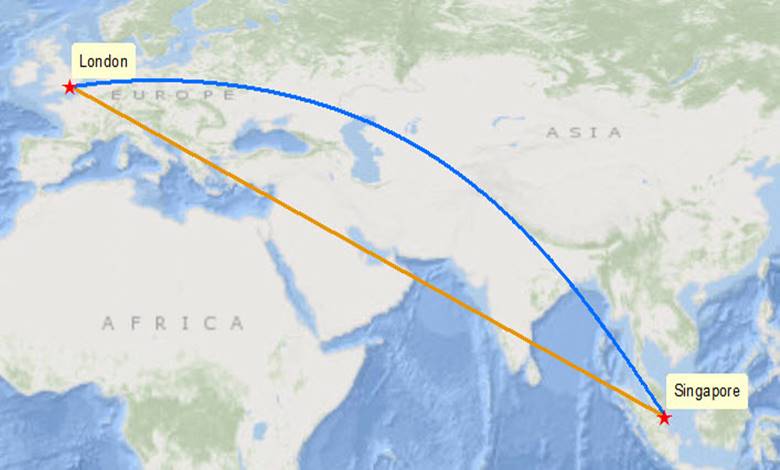
Bir pilot olduğunuzu ve Londra’dan San Francisco’ya uçtuğunuzu hayal edin. Aşağıda solda gördüğünüz haritadan bir rota seçmeniz gerekiyor. Mavi ile işaretlenmiş düz çizgiyi mi yoksa sarı ile işaretlenmiş uzun eğri çizgiyi mi seçerdiniz?
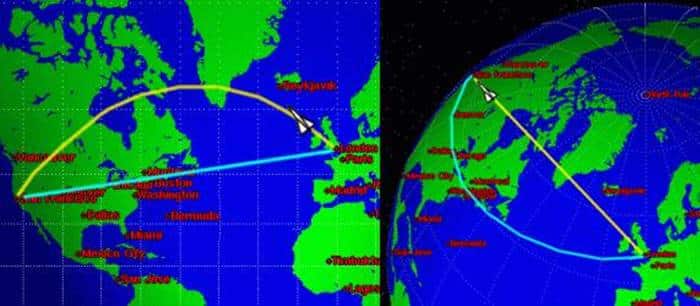
Size mavi olan gibi gelse de aslında eğri çizgi en kısa olanıdır! Bu iki çizgiyi de 2 boyutlu düzleme taşıdığımızda, bu durumun şaşırtıcı doğası daha net ortaya çıkar! Görseldeki gerçek en kısa mesafe çizgisi, doğrusal mesafeden çok daha uzun gözükse de, Dünya üzerinde aslında çok daha kısadır. Sağ taraftaki Dünya resminde büyük daire rotasının (sarı renkli) düz haritada görünenden neden daha kısa olduğunu görebilirsiniz. (Sarı çizgiyi, Dünya’yı çevreleyen daha büyük bir çemberin parçası olarak hayal edebilirsiniz). Konuyu daha iyi anlayabilmeniz için bu noktada büyük daireyi biraz daha açıklamaya çalışalım.
Büyük Daire Nedir?

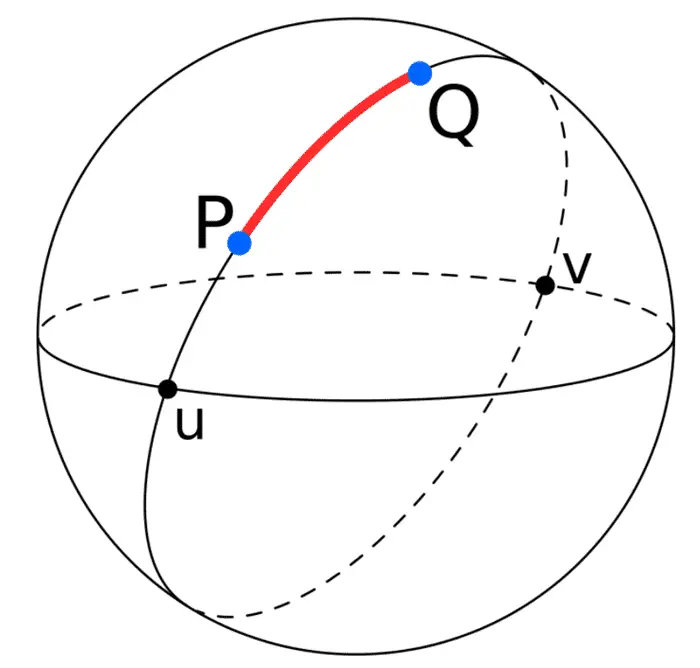
Herhangi bir büyük daire küreyi eşit iki parçaya (yarıküreye) böler. Örneğin ekvator bir büyük daire olarak kabul edilir. Benzer şekilde her bir boylam yayı, tam karşısındaki boylam yayı ile birleştirildiğinde bir büyük daire oluşturur. Aşağıdaki resimde, P ve Q noktaları çap üzerinde olmayan iki noktadır. PQ arasındaki yay en kısa mesafeyi temsil eder. Öte yandan u ve v noktaları zıt kutuplu noktalar olarak bilinir ve büyük çemberi iki özdeş yaya böler.
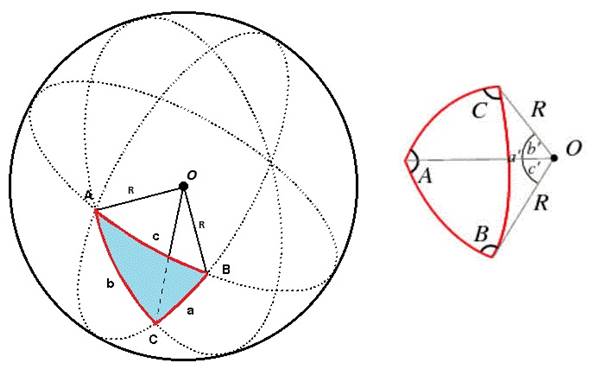
Bir kürenin yüzeyindeki herhangi iki nokta arasındaki büyük çember mesafesini hesaplamak, küresel trigonometri kullanımını gerektirir. Küresel üçgen, bir kürenin yüzeyinde, üç köşede çiftler halinde kesişen üç büyük dairesel yay tarafından oluşturulan bir şekildir. Bir küre üzerindeki şekillerin açılarının ve mesafelerinin incelenmesi ise küresel trigonometri olarak bilinir. Küresel bir üçgenin açılarının toplamı 180° ile 540° arasındadır.
Son olarak büyük çember ile yapılan mesafe ölçümleri bile verilen iki konum arasındaki gerçek en kısa mesafeyi temsil etmez. Çünkü hepimizin bildiği gibi Dünya bir küre olmaya yakındır, ama tam olarak değildir. Aslına bakarsanız Dünya Geoit biçimindedir. Geoit, küre olarak adlandırılan geometrik şeklin iki tarafından basık olan halidir. Dolayısıyla hesaplamalarda yaklaşık ±% 5 hata payı her zaman bulunmaktadır.
Kaynaklar ve ileri okumalar:
- Time and motion; Yayınlanma tarihi: 1 Ocak 1999; Bağlantı: https://plus.maths.org/
- Is A Straight Line Always The Shortest Distance Between Two Points? Yayınlanma tarihi: 22 Ocak 2022. Bağlantı: Is A Straight Line Always The Shortest Distance Between Two Points/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










