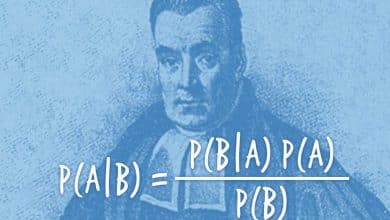Matematik ve müzik farklı dünyalar gibi görünebilir, ancak yüzyıllar öncesine uzanan bir ilişkiyi paylaşırlar. Matematik, müzik gamlarını düzenleme biçimimizden bir enstrümanın sesini belirleyen fiziğe kadar, müziğin özüne işlenmiştir. Hatta tam da bu nedenle, birini öğrenmek, diğerinde ustalaşma yeteneğinizi bile artıracaktır.

Müzik ve matematik arasındaki ilişki her iki yönde de akar. Ünlü bir tabla davulcusu ve şair olan Princeton Üniversitesi’nin önde gelen matematikçisi Manjul Barghava, “Üçünü de düşündüğümde her türlü yaratıcı düşünce bir araya geliyor.” demiştir. Bu sinerji, matematikçilerin yalnızca sol beyinli veya ruhsal ifade yeteneğinden yoksun akademisyenler olduğu yönündeki klişeyi altüst eder.
Matematik, klasik müziğin diğer alanlarında da, tuhaf bir şekilde temsil edilir. Örneğin, Johann Sebastian Bach’ın besteleri 14 ve 41 sayılarıyla doludur. Bu, alfabedeki harflere ayrı sayılar atayan numerolojiye bir göndermedir; yani, A=1, B=2, C=3 vb. Bach’ın ismindeki harflerin sayısal değerlerini topladığımızda — B+A+C+H veya 2+1+3+8 — 14’e eşit olur. Ve 14’ün tersi 41’dir.

Matematik Ve Müzik İlişkisi Nedir?
Öklid’in zamanından (MÖ 325-265) ve hatta daha öncesinden beri, müzik hakkında konuşmanın matematiksel bir yolu olmuştur. Müzisyenler perdeden, yani bir notanın ne kadar yüksek veya alçak olduğundan bahsederler.
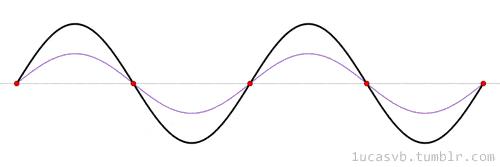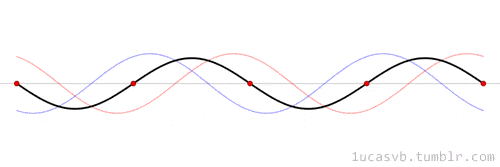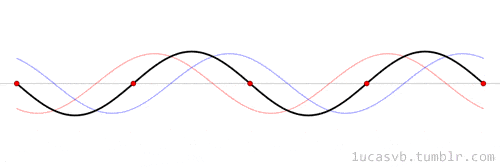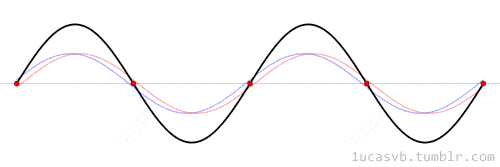
Matematiksel bir açıdan baktığımızda da ses dediğimiz şey aslında sinüs dalgalarının bir karışımından oluşur. Ancak bir sesin parmak izini temelinde bazı şeyler belirler. Bunların en başında da frekans gelir. Dalgaların bir saniyede ileri geri gitme sayısı, o sesin frekansıdır. Sesin frekansı, sesin ne kadar yüksek veya alçak olduğunu belirleyen perdesini belirler.
Bir ses dalgası 1 saniyede 10 salınımı tamamlarsa, frekansı 10 Hz olacaktır. Her frekans için farklı bir sesimiz (farklı bir nota) vardır. Örneğin, La notası 440 Hz’lik bir frekansa karşılık gelmektedir.
Bir nesneye vurursanız, doğal frekansında titreştirildiği için oluşan bir ses duyarsınız. Bu, nesnenin şekli ve yapıldığı malzemeyle ilgilidir. Müzik aletleri, hoş sesler üreten malzemeler ve şekiller kullanarak, bu olgudan yararlanılarak yapılırlar. Aynı nedenle de aynı notayı farklı enstrümanda çalarsak farklı ses duyarız.
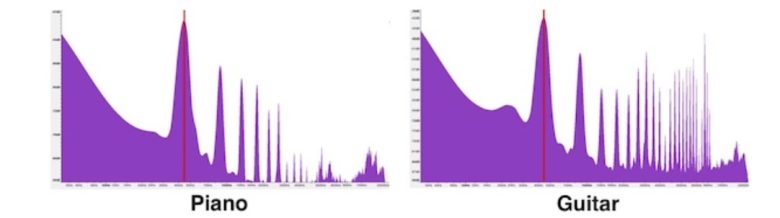
Bir tel titreştiğinde duyduğumuz şey tek bir saf ses değil, frekansları temel frekansın katları olan birkaç sesin üst üste gelmesidir. Temel frekans en çok katkıda bulunan ana frekanstır ve diğer çoklu frekanslara
harmonikler denir. Temel bir frekansa harmoniklerin eklenme oranı, her enstrümanın karakteristik tınısının üretilmesine katkıda bulunur. Bu nedenle, örneğin mızıka flütten farklı bir sese sahiptir.
Pisagor
Frekans kavramı keşfedilmeden önce matematikçiler belirli bir notayı üretecek telin uzunluğundan bahsediyorlardı. Hatta bir telin değişik boyları ile değişik sesler elde edildiğini ortaya çıkartan ilk kişi Pisagor‘dur.

Gergin bir teli uçlarına bağlı olarak hayal edin. Bu ipi çaldığımızda titreşir. Pisagor bu teli iki parçaya bölmeye karar verdi. Çıkan ses tam olarak aynıydı, sadece daha yüksekti. Pisagor burada durmadı. Telin 3 parçaya bölünmesi durumunda sesin nasıl olacağını merak etti.
Sonuç yeni bir ses, yani farklı bir notaydı. Ayrıca bu ses, farklı olmasına rağmen, önceki sesle iyi bir şekilde birleşerek kulağa hoş bir armoni yaratıyordu. Sonunda çalışmaya devam etti ve sesleri matematiksel olarak birleştirerek gamlar oluşturdu. Bu da daha sonra bu gamları yeniden üretebilen müzik aletlerinin yaratılmasına ilham verdi.

Armoniler bize neden hoş gelir?
Aynı anda iki farklı nota çaldığımız zamanlarda, ortaya çıkan ses bazen hoş bazen de itici gelir. Hangi kombinasyonların birlikte iyi duyulduğunu oktavları ile ilgilidir. Oktav, müzikte bir sesin frekansının iki katına ya da yarısına denk gelen nota aralığıdır.
İki ses arasındaki frekans farkı tam olarak iki kat olduğunda, bu sesler arasında bir oktav farkı vardır. Örneğin, A4 notası ( La) 440 Hz frekansına sahiptir. A5 notası ise bu frekansın iki katı olan 880 Hz frekansında çalınır ve A4 ile A5 arasında bir oktav farkı bulunur.
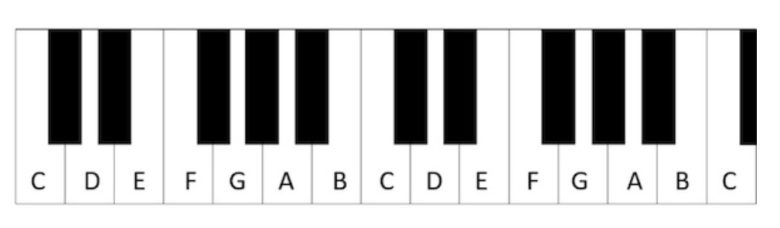
, ikinci C (bir oktav daha yüksek) 2f frekansına sahip olacaktır. Bir sonraki C’ye ulaşmak için C 2 f’yi alıp bir kez daha 2 ile çarpmamız ve C 4f’ye ulaşmamız gerekecektir. İşlemi tekrarlayarak, o piyanonun son C’si C 8f olacaktı
Aralarında bir oktav bulunan iki nota aynı isimle adlandırılır ve sanki aynı notaymış gibi ses çıkarırlar. Ancak biri daha yüksek, diğer ise daha alçaktır. Bir oktav aralıklı notalar çaldığımız zaman, bir notanın frekansı, diğer notanın frekansının iki katı olacaktır ve bu nedenle iki notanın frekansı arasındaki oran 1:2’dir.
İlginçtir ki, insan beyni genel olarak bir kesrin pay ve paydasındaki 2/3, 4/5, 8/5 vb. gibi küçük değerlerden gelen sesleri “hoş” olarak yorumlar. 32/45 kesri ise kulağa itici gelecektir.
Diğer bir deyişle, aynı anda iki notayı çaldığımızda, saniyede X kez duyulan bir sesi, saniyede Y kez duyulan başka bir sesle karşılaştırıyoruz ve bunun sonucunda X/Y oranı ortaya çıkıyor. Sonuç küçük sayılarla sonuçlanıyorsa, sesi yorumlamamız daha kolay olacaktır.
Sonuç Olarak
Müzikteki çeşitli sorular için birçok başka matematiksel açıklama vardır ve bunları burada göstermek için Fourier serisi gibi daha ileri konulara değinmek gerekecektir. Bu dönüşüm adını Fransız matematikçi ve fizikçi Jean Baptiste Joseph Fourier’den alır.
Bir Fourier serisi, fizikte bir dalganın davranışını tanımlamak için kullanılabilir. Fourier’in çalışmasının gösterdiği şey, karmaşık dalgaların, farklı frekans ve genliklerdeki bir dizi sinüs dalgasının birbirine eklenmesi ile ortaya çıktığıdır.
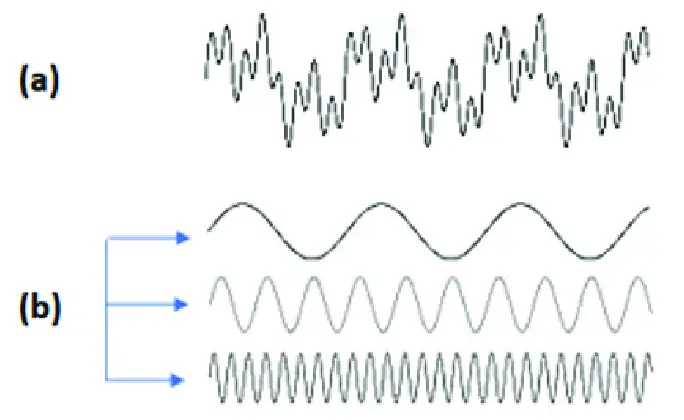
Bu yöntemlerini kristalografi, optik, sinyal işleme ve jeofizik gibi alanlarda son derece değerli hale getirir. Dilerseniz bu yazımızda detaylara göz atabilirsiniz: Fourier Dönüşümü: Basit Bir Formül Dünyayı Nasıl Değiştirdi?
Kaynak ve ileri okumalar:
- Why Do Different Musical Instruments Make Different Sounds?; Kaynak site: Science ABC. Yayınlanma tarihi: Bağlantı: Why Do Different Musical Instruments Make Different Sounds?/
- Maths in a minute: Maths and music; yayınlanma tarihi: 2 Kasım 2021.Kaynak site: Plus Math. Bağlantı: Maths in a minute: Maths and music;/
- Musical numbers: Math and music nurture a deep and complex relationship. Yayınlanma tarihi: 27 Nisan 2023. Bağlantı: Musical numbers: Math and music nurture a deep and complex relationship
Matematiksel