Dünya görüşümüz ve bunun sonucunda ortaya çıkan eylemlerimiz genellikle, 150 yıldan fazla bir süre önce bir İngiliz matematikçi Thomas Bayes tarafından tasarlanan basit bir teorem tarafından yönlendirilir. Bayes Teoremi, II. Dünya Savaşı sırasında Enigma kodunu kırmak için kullanıldı. Günümüzde ise bilim, teknoloji, tıp ve çok daha fazlasındaki belirsizliği yönetiyor.
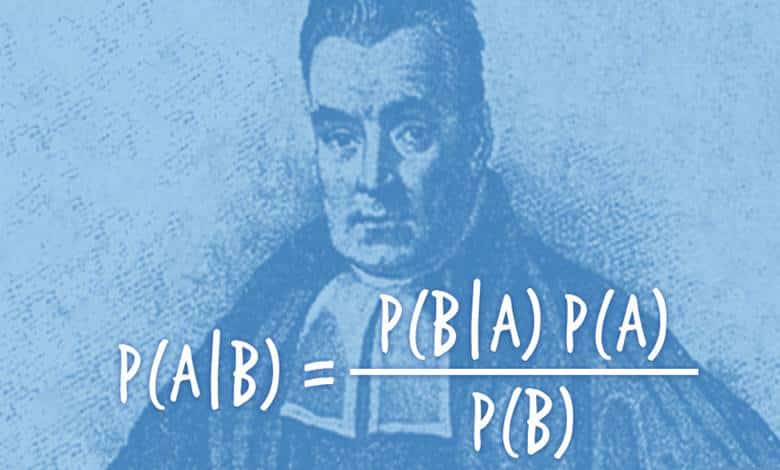
Belirli bir kanser türünün nüfusun %1’ini etkilediğini varsayalım. Bu kanser için piyasa bir test var ama güvenilirliği mükemmel değil. Bu test kanserli kişilerin %90’ında pozitif sonuç veriyor yani doğru tanı koyuyor. Ancak aynı zamanda kansersiz kişilerin %5’inde de pozitif sonuç veriyor. Diğer bir deyişle bu kişiler de kanser olmadığı halde kanser olduğunu ortaya koyuyor. Endişelendiniz ve bir test yaptınız. Sonucunuz ne yazık ki pozitif çıktı. Bu durumda kanser olma olasılığınız nedir?
Çoğumuz kanser olma ihtimalimizin %90 olduğunu söyleriz. Ancak bu doğru değil. Aslında kanser olma ihtimaliniz %15 civarında. Bunun nedenini öğrenmek için Bayes teoremini anlamalısınız..

Bayes Teoremi, 18. yüzyılda Thomas Bayes tarafından öne sürülmüştü. Ancak kendisi bu teoremi öne kurguladığında çok da yayınlanmaya değer olduğunu düşünmüyordu. Bu nedenle üyesi olduğu Kraliyet Cemiyetine bile sunmamıştı. Aslında teorem ününü onun ölümünden sonra kazanmıştır.
Bayes Teoremi Nedir?
Aslında Bayes teoremin nedir? sorusunun cevabını iki farklı biçimde vermemiz gerekir. Bunlardan ilki bir formül ve matematiksel bakış açısı ile olacaktır. İkincisi ise Bayes’ci düşünmenin ne anlama geldiğidir. Önce matematiksel tanımla başlayalım.
Bu bakış açısında koşullu olasılık konusunu anımsamalısınız. Koşullu olasılık kavramı, bir olayın gerçekleşme olasılığının hesaplanmasında ek bilginin kullanılmasına da olanak tanır. Bayes teoremi, iki olayın koşullu olasılığını ilişkilendirmemizi sağlar. Örneğin, yazının başında verdiğimiz örneğe dönersek pozitif test sonucu verildiğinde bu kansere sahip olmanın koşullu olasılığını P( kanser | pozitif test sonucu)olarak yazardık.
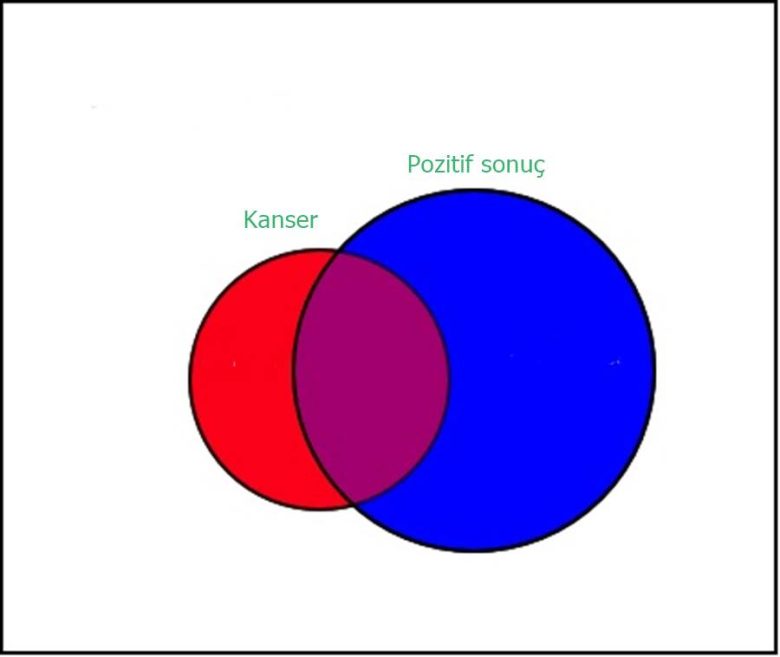
Testi yaptırmadan önce bu kansere yakalanma olasılığınızın P(kanser)=0,01 olduğuna inanıyordunuz. Yani 10.000 kişilik bir nüfusta 100 kişinin bu kansere sahip olmasını beklersiniz. Bunu aşağıdaki şemada kırmızı ile gösterelim. Testi yaptırdınız ve artık elinizde bir sonucunuz var. Peki ama 10.000 kişilik bir grupta kaç kişinin test sonucu pozitif çıkacak? Bunu da mavi ile gösterelim. Kanser hastasıysanız test sonucunun pozitif çıkma ihtimali %90’dır. Bu kişiler de kesişim kümesinde yer alsın.
Ancak bu testin aynı zamanda kansersiz kişilerin %5’inde de pozitif sonuç verdiğini anımsayın. Yani popülasyonumuzdaki 9.900 kansersiz hastadan 495’inin testi yanlışlıkla pozitif çıkacak. Bu kişiler de resimdeki kırmızı dairenin dışındaki mavi dairenin içinde yer alıyor. Bu durumda 10.000 kişi içinden 90+495=585 kişinin sonucunun pozitif olması gerekiyor.
Peki test sonucunuz pozitif çıktığına göre bu kansere yakalanma olasılığınız nedir? Bu, kanser hastası olan ve test sonucu pozitif çıkan kişilerin (iki dairenin kesişimi) pozitif test sonucu olan tüm insanlara (mavi daire) oranıdır. Yani 90/585 = 0,154 diğer bir deyişle % 15 tir. Bu sonuç Bayes Teoremi olarak bilinir ve daha genel olarak aşağıdaki gibi yazılır.
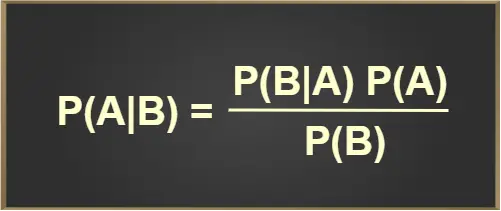
Bayes Teoremi Günlük Hayatımızda Her Yerdedir
Bayes Teoremi mevcut olan bilgiyi ek bilgi ile birleştirmek için kullanılır. Bunun anlamı yeni bilgilerin toplanması, ardından eski olasılık tahminlerinin yeniden gözden geçirilmesidir. Bayes teoreminin altında yatan temel mantık yeni kanıtların önceki inançları güncellemesidir.
Hepimiz yaşantımızda günlük olaylara olasılıklar atamak ve yaşamlarımızı yönetmek için deneyimlerimizden ve anılarımızdan edindiğimiz ön bilgileri ve duyularımızdan gelen yeni kanıtları kullanırız. Durum böyle olunca da farkında olmadan Bayesci düşünceyi uygularız.
Örneğin, bir mekanda dart oynuyorsanız ve yakınınızdaki bir yabancı kendisinin profesyonel bir dart oyuncusu olduğunu söylüyorsa, başlangıçta kişinin şaka yaptığını varsayabilirsiniz. Sonuçta bu kişi bir dart atıp hedefi vursa bile bu sizi yine de etkilemeyebilir. Ancak eğer o kişi arka arkaya on kez hedefi vurursa, onun profesyonel olma iddiasını kabul etme eğiliminde olursunuz. Kanıtlar biriktikçe önceki inancınız geçersiz kılınacaktır. İşte burada Bayes Teoreminin ardındaki mantık iş başındadır.
Bayesci yaklaşımlar, belirsiz verilerden kesin bilgiler çıkarmamıza, geniş bir olasılıklar evreninden dar çözümler bulmamıza olanak tanır. Yazının başında bahsettiğimiz İngiliz matematikçinin Alan Turing‘nin Alman Engima kodunu kırması da bu sayede olmuştur.
II. Dünya Savaşı’nın patlak vermesiyle birlikte Alan Turing, Almanlar tarafından geliştirilmiş olan ve Alman Ordusu’na ait gizli mesajların şifrelenmesinde kullanılan Enigma adlı şifreleme mekanizmasının çözülmesi için yapılan çalışmalara katılmıştı.

Almanlar Enigma makinesi ile hassas askeri bilgileri, örneğin ölümcül U-boat denizaltılarının konumlarını içeren önemli mesajları şifreliyorlardı. Bunu yapmak için kullandıkları algoritma her 24 saatte bir değişiyordu. Bu yüzden en zeki şifre kırıcılar için bile bu mesajları çözmek neredeyse imkânsızdı.
Turing’in Bayesci içgörüsü, belirli mesajların diğer mesajlardan çok daha olası olduğuydu. Örneğin her mesaj aynı açılış metni, bir mesaj numarası ile başlıyordu. Mesajlar genellikle hava durumu raporları gibi rutin bilgileri şifreliyordu. Bu ön bilgiler, değerlendirilmesi gereken olası seçenekleri azalttı ve bu sayede Turing’in şifre kırma makinesi, Enigma kodunu çözdü.
Bayes Teoremin Kötüye Kullanımı Mümkün müdür?
Evet mümkündür ve tarih bunun örnekleri ile doludur. Sonucunda öncül bilgi çoğu zaman bir tahminden ibarettir ve bu durum öznel faktörlerin hesaplamalara karışmasına izin verir. Mahkemelerde bu, ciddi adli hatalara yol açar. ((bkz: savcının yanılgısı). Bunun en bilinen örneği Sally Clark 1999’da iki çocuğunu öldürmekten haksız yere suçlu bulunmasıdır.

Sonuçta bir ailede bir çocuk ani bebek ölümü sendromu sonucunda öldüyse, genetik bir yatkınlık olabileceğinden, başka bir çocuğun ölme olasılığı artık eskisinden daha fazla olacaktır. Ancak bu sonuç yine çok küçüktür. Davada dikkate alınmayan şey, bir annenin iki çocuğunu öldürme olasılığının da çok çok küçük olmasıdır. Bu, Bayes Teoreminin zayıf anlaşılmasının geniş kapsamlı sonuçlara yol açabileceğine bir örnektir.
Sonuç Olarak
Benzer şeyleri bir arada gruplandırmak, yani kategorize etmek, dünyayı anlamlandırma şeklimizin önemli bir parçasıdır. İnsanlarla, nesnelerle veya hayvanlarla her etkileşim kurduğumuzda, ne yapacağımızı bilebilmek için kategorileri hakkında öğrendiğimiz bilgileri kullanırız. Ayrıca kafamızda bir kategorinin “ortalama” üyesinin neye benzediğini anlamak için bilinçsiz zihinsel istatistikler vardır.
Ancak kategorilere olan güvenimiz, farkında olmasak bile kolayca önyargıya dönüşebilir. Bu önyargılardan kaçınmak zordur. Bayes teoremi ve beraberince gelen düşünme biçimi bu önyagılardan kurtulmak için bir seçenektir.
Kaynaklar ve ileri okumalar
- John Horgan; Bayes’s Theorem: What’s the Big Deal?; Yayınlanma tarihi: 4 ocak 2016; Bağlantı: https://blogs.scientificamerican.com/
- Maths in a minute: Bayes’ theorem; yayınlanma tarihi: 25 Ocak 2016; Bağlantı: https://plus.maths.org/
- Bayes’ Theorem: the maths tool we probably use every day, but what is it?. Yayınlanma tarihi: 23 Nisan 2017. Bağlantı: Bayes’ Theorem: the maths tool we probably use every day, but what is it?
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










