Fourier dönüşümleri, kullandığımız elektronik aletlerin görsel ve işitsel sinyalleri işlemesini mümkün kılar. Bilgisayarınıza bir şarkı indirdiğinizde veya MP3 çalarınızda bir dijital müzik dosyası çaldığınızda da Fourier dönüşümü formülünü kullanırsınız. İnternette gördüğünüz fotoğrafları JPG formatına dönüştüren, hatta ses geçirmez kulaklıklarınızın çalışmasını sağlayan da bu denklemdir.

1940’lı yıllara kadar televizyonlar siyah-beyazdı. Ardından 1950’lerde Amerika’da ilk renkli televizyon satışları yapıldı. Televizyonların neden siyah-beyaz olduğunu hayatınızın bir döneminde eminim merak etmişsinizdir. Cevap ise basittir. Renkli yayın yapabilmek için televizyonların kırmızı, yeşil ve mavi ışık verilerini bir arada işlemesi gerekir. Televizyonların bunu yapabilmesinin yolu ise elbette matematikten geçer.
Basitçe Fourier Dönüşümü Nedir?
Fourier dönüşümleri, elektronik cihazlarımızın görsel ve işitsel sinyalleri işlemesini mümkün kılan matematiksel dönüşümlerdir. Bu dönüşümler, temelde karmaşık dalgaları basit sinüs dalgalarına ayırmaktadır. Ayrıca Fourier dönüşümleri basit dalgaları daha karmaşık hale getirmemizi de sağlamaktadır.
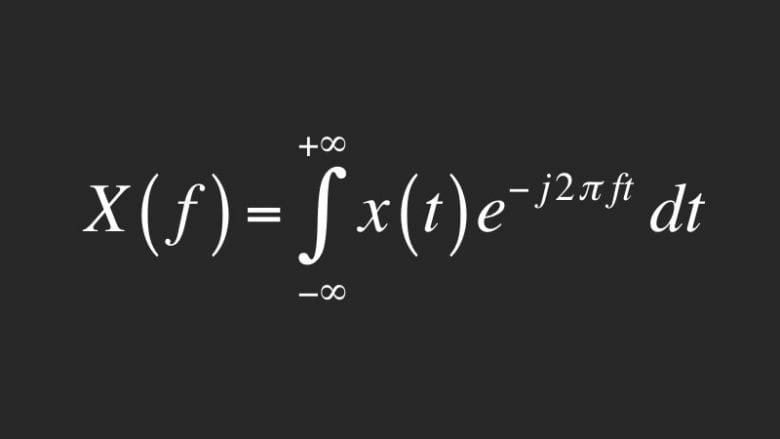
Aslında yaptığı şey oldukça basittir. Zor görünmesinin nedeni de formülde karşımıza çıkan ifadelerdir. Elinizde bir kağıt banknot varsa ve minibüse bindiğiniz zaman şoförün bu paraya itiraz edeceğini bilirsiniz. Bu nedenle de paranızı bir yerlerde bozdurmak zorunda kalırsınız. Bir kağıt para karşılığında bir sürü bozuk para elde edersiniz. Harcamanızı yaptıktan sonra da bozuk paralarınızı bir yerlerde yeniden bütünlersiniz.
İşte Fourier Dönüşümü de tam olarak aslında bu işi yapar. Ancak paralar ile değil bu sefer dalgalar ile uğraşır. Karmaşık dalgaları alır ve basit sinüs dalgalara ayırır. Daha sonrasında da basit dalgaları tek bir karmaşık dalga olacak biçimde birleştirir. Bir Fourier dönüşümü zamanı, frekansa eşitlemektedir. Örneğin bir piyona parçasından çıkan dalgaları düşünelim. Oluşan dalgalar zamana bağlı birer sinyaldir. Ancak bu dalgaların bir de frekansı vardır.
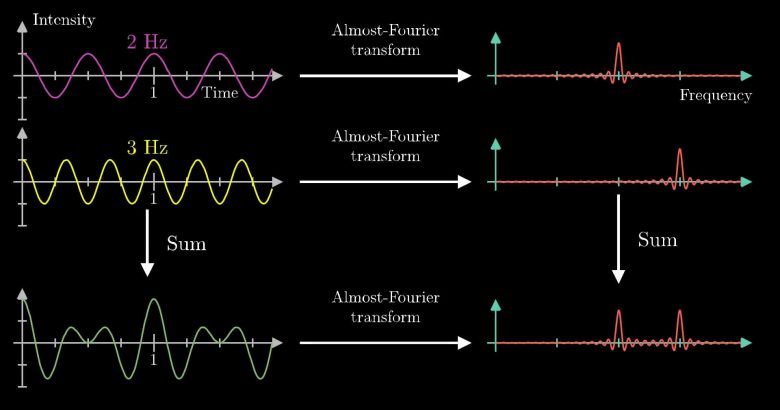
Fourier dönüşümü sinyalleri frekanslarına göre filtrelememize veya yayın kanallarını yönetmemize izin verir. Bu dönüşümler bize gerçekten şeylerin doğası hakkında çok fazla fikir veriyor. Bunların hepsi, sinyallerin zamanda nasıl geliştiğini düşünürsek anlaşılması zor kavramlardır.
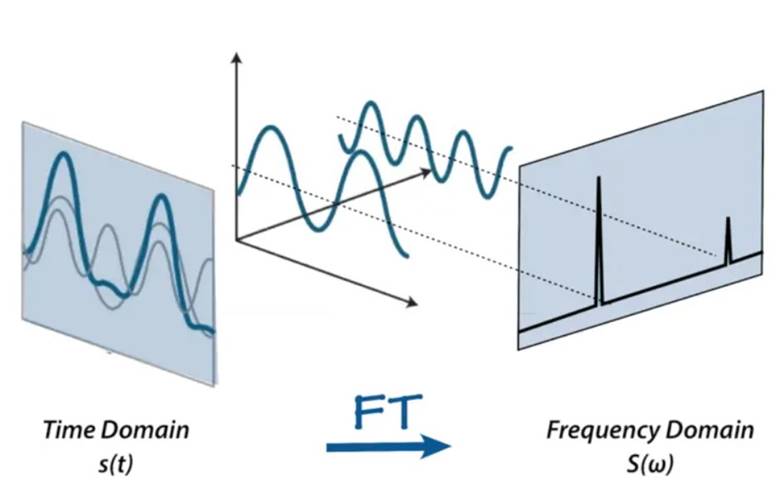
Ancak bunları karşılık gelen frekans bileşenleri açısından düşünürsek çok daha açık ve sezgiseldirler. Arka plandaki matematik hakkında ek bilgi almak isterseniz bu yazımıza göz atmalısınız: Fourier Serisi: Basit Bir Buluş Birçok Sırrın Kilidini Nasıl Açtı?
Fourier Dönüşümleri Neden Önemlidir?
Video, ses, sinyal ve grafik uygulamaları için sürekli olarak Fourier dönüşümleri kullanılmaktadır. Filtreleme, ayrık Fourier dönüşümü için bir kod satırı kullanılarak dijital olarak yapılmaktadır. Bu da dirençleri, transistörleri ve indüktörleri kullanmanın analog işleminden çok daha basittir.
Sinyaller frekans açısından temsil edildiğinde, farklı frekansları bastırabilir veya güçlendirebilirsiniz. Verileri sıkıştırmak için matematiksel işlem de kullanılabilir. Örneğin, küçük bir akıllı telefonda binlerce şarkıyı saklamayı mümkün kılan .mp3 dosyalarını kodlayabilirsiniz. Çok daha büyük olan WAV dosyalarıyla ise bunu yapamazdınız.
Fourier Dönüşümleri Elektronik Cihazlarda Nasıl Çalışır?
Veri iletişiminde, cihazlar ayrı bir sesi, bir müzik parçasını veya başka bir bilgi türünü bir dizi 1 ve 0’a dönüştürür. İlk olarak, elektronik cihazlar sinyalleri örneklemektedir. Sesi yüksek kalitede tutmak için, örnekleme frekansı, gelen en yüksek frekansın en az iki katı olmalıdır. Konuşma ve müzik 20 kHz’in altında frekanslara sahip olduğundan, CD’ler sesi 44,1 kHz’de örneklemektedir.

Ses programcıları, seslerin nasıl algılandığını bilgi olarak kaydedip veri gereksinimlerini 10 veya 20 kat azaltan algısal ses kodlamasını kullanarak yer tasarrufu sağlarlar. Böylece cihazın beklenenden 10 ya da 20 kat daha ses dosyası depolaması mümkün olmaktadır.
Fourier Dönüşümü Makine Öğreniminde Nasıl Kullanılır?
Makine öğreniminde (ing: machine learning), bilgisayarlar verileri 1 ve 0 olarak sınıflandırır. Fiziksel dünyaya dayanan bir ses veya görüntü gibi bir bilgi parçasını alırlar, sayısal bir biçime dönüştürürler ve sayıları depolanan veri kümelerindeki bilgilerle karşılaştırırlar. Bu, bilgisayarların örneğin fotoğraflardaki yüzleri tanımasına olanak tanır.
Makine öğrenimi teknikleri geliştiren uzmanlar, mümkün olduğunca önemli ve sayısal olarak basit özellikler bulmaya çalışmaktadırlar. Çünkü bu, hesaplamayı basitleştirir ve depolama alanından tasarruf sağlar. Sesler için bu bilginin frekans bileşenlerine dayanması muhtemeldir, bu nedenle Fourier dönüşümleri bu sınıflandırma kullanılmaktadır. Örneğin bir bilgisayar birinin sesini tanımaya çalışıyorsa Fourier dönüşmleri sayesinde bunu başarabilir.
Kulaklarımız da Fourier Dönüşümlerini Kullanıyor!
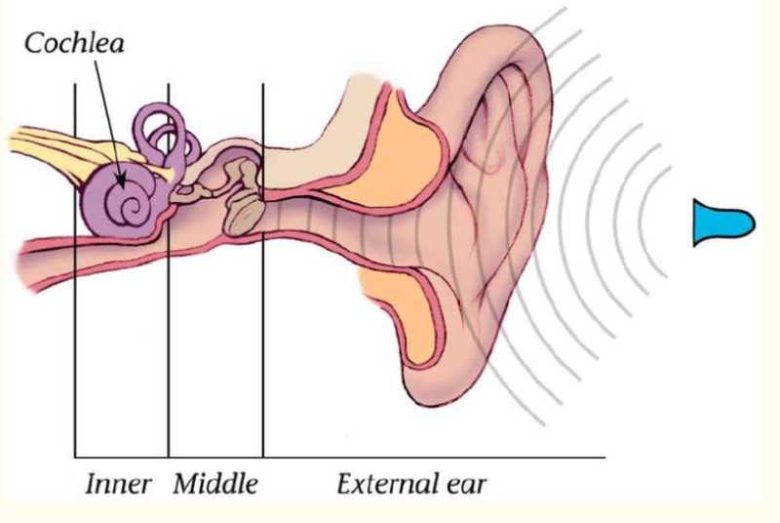
Sesleri, bilgisayarların onları analiz etmeyi öğrenme şekline benzer şekilde sınıflandırırız. Sesleri birçok özelliğinin yanı sıra frekanslarına göre de algılıyoruz. Kulaklarınızdaki işitsel sistem, kokleanızda mekanik olarak bir Fourier dönüşümü gerçekleştirir. Böylece gürültülü bir ortamda belli seslere odaklanabilir ve sesleri birbirine karışmadan duyabilirsiniz.
Kaynaklar ve İleri Okumalar
- Fourier Transforms: The Math That Made Color TV Possible ; Bağlantı: Understanding Fourier Transforms: The Math That Gave Us Color TV (popularmechanics.com) ; Yayınlanma tarihi: 14 Şubat 2023
- Digital Music Couldn’t Exist Without the Fourier Transform; Yayınlanma tarihi: 30 Mayıs 2016; Bağlantı: Digital Music Couldn’t Exist Without the Fourier Transform/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel








