Matematikte bir problemi çözmek için tasarlanmış, ancak daha sonra diğer birçok problemi çözmek için kullanılmış bir en güzel örneklerinden biri Fourier serisidir. Bu seriye adını veren efsanevi matematikçi de Joseph Fourier’dir.

Efsanevi derken abartmıyoruz. Kendisi Napolyon’a Rosetta taşını bulmak için yaptığı Mısır gezisinde eşlik etti. Isı transferi anlayışında devrim yarattı. CT ve MRI tarama görüntüleri oluşturmak için günümüzde kullanılan matematiksel araçları geliştirdi ve sera etkisini keşfetti. Bu nedenle ilk etapta kısaca kendisini tanımalısınız.
Joseph Fourier Kimdir?
Fourier 1768’de Fransa’da doğdu. Din adamı olarak eğitim aldığı halde, hayatının uzun bir dönemini Ecole Polytechnique gibi Fransız üniversitelerinde matematik öğreterek geçirdi. Fransız devriminde aktif rol aldı ve bu nedenle iki kez hapse atıldı. Napolyon’un danışmanlığını ve 1804-1807 yıllan arasında Grenoble valiliğini yaptı. 1817 ‘de Bilimler Akademisi’nin sekreterliğine seçildi.
Tüm bu yoğunluğun arasında da bir dizi matematik ile ilgili makale yayınlamayı başardı. Mühendislerin her gün kullandıkları bazı denklemler ve ısı transferi katsayıları gibi kavramlar onun arta kalan zamanlarında yaptığı bu çalışmalar sayesinde hayatımıza dahil olacaktı.

19. yüzyılın başında metal işleme sektörünün ihtiyaçları nedeniyle gezegenin iç sıcaklığı konusuna olan ilgi artmıştı. Bu dönemde bilimde ısı akışı büyük önem kazanmıştı. Dünyanın derinlerdeki sıcaklığını doğrudan ölçmek imkânsız olduğundan, geriye dolaylı yöntemler kalıyordu. Bu nedenle çeşitli bileşimlere sahip cisimlerde ısının ne şekilde aktığını anlamak şarttı.
Joseph Fourier de bu dönemde ısının katı bir nesneden nasıl yayıldığı sorununu çözmeye çalışıyordu. Sonunda kenarlarından birine bir ısı kaynağı uygulandıktan sonra nesnenin, herhangi bir zamanda ve yerdeki sıcaklığını hesaplamasına izin verecek bir yaklaşım geliştirdi.
Fourier, yaşamı boyunca Fransız Bilim Akademisi’ne seçilmek de dahil olmak üzere pek çok ödül aldı. Mayıs 1830’da 63 yaşındayken anevrizmadan hayatını kaybetti.
Isı transferi İle İlgili Çalışmaları Sonucunda Fourier Serisini Bulacaktı
Fourier’in yaptığı ilk iş, ısı akışı için kısmi türev denklemi elde etmek olmuştu. Denklemi basitleştirmek için çeşitli kabuller yapmıştı. Örneğin cisim homojen olmalı (özelikler, cismin her noktasında aynı olmalı) ve izotropik olmalıydı. ( Yani cismin her yönünde davranışlar birbirinin aynı olmalı). Bu şekilde, günümüzde ısı denklemi dediğimiz diferansiyel denklemi buldu.
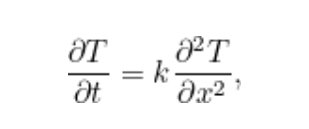
Isı denklemi, üç-boyutlu bir cismin herhangi bir noktasında sıcaklığın zamana göre değişimini verir. Denklemin çözümü T(x,t) nesnenin x noktasındaki ve t zamanındaki söyleyecektir. Bu denklemde yapılan küçük bir değişiklik karşımıza hiç beklenmedik sonuçlar çıkarmıştır.
Fourier öncelikle T(x,t) ifadesini basit fonksiyonların toplamı olarak olarak yazabileceğini düşündü. Yani çözümü adım adım yapacak, önce bu fonksiyonları çözecek, sonuçta da aradığı cevaba ulaşacaktı. İkinci olağanüstü kavrayışı, sıcaklığı oluşturmak için fonksiyon seçimindeydi. Seçimi, trigonometride ortaya çıkan sinüs ve kosinüs fonksiyonlarını kullanmaktı. Tüm bunların sonucunda denklemi aşağıdaki biçimde ifade etti.
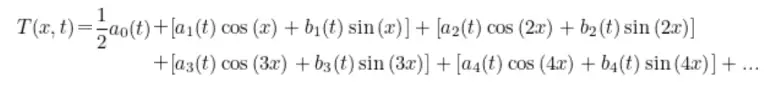
Denklemde gördüğünüz a0(t), a1(t), a2(t), b0(t), b1(t) ve diğerleri kesin değeri başlangıç koşullarına bağlı olan katsayılardır. Bu gösterim biçimi günümüzde Fourier serisi olarak adlandırılıyor. Aşağıda an(t) ve bn(t) ise aşağıda gördüğünüz formül ile belirleniyor. Formüldeki An ve Bn başlangıç koşullarına bağlı olarak değerler alıyor.
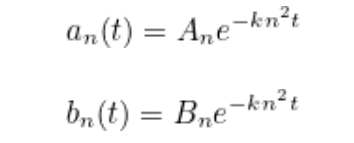
İlk bakışta yukarıdaki denklem size bir anlam ifade etmeyecektir. Ancak bu denklem kesinlikle doğru seçimdi. Fourier’in bu çalışmasından evvel, ısı denklemlerine genel bir çözüm yoktu. Her ne kadar parçalı yaklaşımlar olsa da yeterli değildi çünkü bu yaklaşımlar ısı dağılımının basit denklemlere göre dağıldığını varsayaraktan probleme yaklaşıyordu.
Fourier Serisi Ne İşe Yaradı?
Bu gösterim biçimi sayesinde problem artık çok daha basit problemlere bölünmüştü. Fourier’in kavrayışından kısa bir süre sonra, bir fonksiyon oluşturmak için sinüs ve kosinüs kullanımının çok sayıda başka sorunu çözebileceği anlaşıldı. Bunların arasında dalgaların hareketi, gazların davranışı, yerçekimi, elektrostatik, elektromanyetizma ve hatta borsanın davranışındaki birçok problem vardır.
Fizikteki birçok problem, titreşimler ve salınımlar içerir. Çoğunlukla yaylar, sarkaçlar, harmonik dalgalar gibi salınım hareketleri basittir. Bu hareketler sinüs veya kosinüs fonksiyonları olarak kolayca gösterilir. Bununla birlikte, birçok durumda (elektromanyetizma, ısı iletimi, kuantum teorisi vb.) dalga formları basit değildir. Yani onları bilinen sinüs ve kosinüs fonksiyonlarına dönüştürmek kolay değildir.
Fourier serisi, bir fonksiyonun sonsuz bir dizi sinüs ve kosinüs fonksiyonu olarak ifade edilebilmesini sağlar. Yani basit bir ifadeyle Fourier serisi kendi başına üzerinde çalışılması zor periyodik fonksiyonları alır ve sonra onu başa çıkması daha kolay olan bir grup sinüs ve kosinüs fonksiyonu olarak ayırır.
Fourier, doğanın derinlemesine incelenmesinin matematiksel keşiflerin en verimli kaynağı olduğunu söylerdi. Bununla birlikte, oluşturduğu matematiksel kuram pek çok farklı alanda işe yaradı. Bugün Fourier Serisi matematiği yanı sıra, fizik ve mühendislik çalışmalarında temel bir rol oynamaktadır.
Sonuç olarak
Fourier serilerinin modern halini Joseph Fourier geliştirmese de onun onuruna, trigonometrik serilerde yaptığı önemli buluş adıyla anılmaktadır. Dalgalar yoluyla enerji aktarımı ile uğraşan hemen hemen her bilim dalı Fourier’in ortaya koyduğu yöntemleri kullanır. Örneğin günümüzde radyologlar hastaların bakımına yardımcı olurken, Fourier dönüşümüne güveniyorlar. Bu arada Fourier, genel olarak bugün sera etkisi dediğimiz şeyi fark eden ilk bilim insanı olarak kabul edilir.
Bugün Fourier’in adı Eyfel Kulesi’nde yazılıdır. Ama daha da önemlisi, Fourier serisinde ve Fourier dönüşümünde ölümsüzleştirilmiş olup, matematiğin evrenin anahtarı olduğunu bize bir kere daha hatırlatmaktadır.
Kaynaklar ve İleri Okumalar:
- Maths in a minute: Fourier series. Kaynak site: Plus Maths. yayınlanma tarihi: 28 Kasım 2016. Bağlantı: Maths in a minute: Fourier series/
- lan Stewart; Taming The Infinite:The Story Of Mathematics; ISBN 978-605-171-373-1
- In his 250th birthday, Joseph Fourier’s math still makes a difference. Yayınlanma tarihi: 21 Mart 2018. Kaynak site: Conversation. Bağlantı: In his 250th birthday, Joseph Fourier’s math still makes a difference
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










