Büyük matematikçi Isaac Newton, gökkuşağının renklerinin oluşma nedenini ilk açıkladığında şair John Keats dehşete düştü. Keats (tabii ki şiir yoluyla) matematiksel bir açıklamanın ondaki tüm şiirselliği yok ettiğini ve böylece onun gizemindeki büyüyü bozduğunu kaleme aldı. Ancak birazdan göreceğimiz gibi, yalnızca çizgilerin ve dairelerin temel geometrisini gerektiren matematiksel bir açıklama, en az gökkuşaklarının kendisi kadar zariftir.

Güneş’ten gelen ışık dalgaları, farklı dalgaboylarının (gökkuşağını oluşturan renklerin) bir karışımıdır. Bu frekans karışımı aynı anda gözünüze çarptığında beyaz görürsünüz, ancak gözünüz tek başına bir dalgayı yakaladığında belirli bir rengi algılarsınız. Havanın içi her an bu enformasyon keşmekeşiyle doludur. Her dalga diğerleriyle iç içedir. Gördüğümüz dünya, dalga spektrumunun daracık bir aralığı olan gökkuşağının görünür renklerinden ibarettir.
Güneşin ışığı dünyanızı aydınlatır. Fakat bize ulaşan ışık, akkor halindeki Güneş’i terk eden ışıkla aynı değildir. Atmosfer uzun kızılötesi dalgaboylarını ve daha kısa morötesi dalgaboylarının çoğunu emmiştir. Fakat görünür-ışık etkilenmeden yoluna devam eder. Atmosfer yeryüzüne ulaşmaya hak kazanan dalgaları seçmiştir. Bunlar aynı zamanda gözümüzün görmeye evrildiği dalgalardır. Gökkuşağının oluşması ise bu süreçte yaşanan kırılmaların bir sonucudur.
Gökkuşağı Nasıl Oluşur?
Detaylara geçmeden önce çok basit bir deney yapalım. Bir boş bardağın dibine bir madeni para koyun Sonrasında da kafanızı parayı görmeyeceğiniz bir açıya getirin. Parayı görmemenizin nedeni paraya çarpıp gözünüze ulaşan ışının olmamasıdır. Şimdi bardağı ve kafanızı oynatmadan bardağı suyla doldurun. Bu sefer aynı yerde olmasına rağmen parayı görebileceksiniz. Çünkü paradan gelen ışınlar suyun yüzeyini terk ederken yön değiştirdiğinden, artık gözünüze ulaşabiliyorlar.
Bu olay, ışığın suda yavaşladığının dolaylı bir göstergesidir. Işık havaya çıkarken tekrar hızlanır
ve bu yüzden dalganın yönü kırılır. Gökkuşağının renkleri de buna benzer kırılmalar sonucunda oluşmaktadır. Bir güneş ışını küresel bir su damlacığına çarptığında, bir kısmı damlanın yüzeyinden yansır, bir kısmı ise içine girer. Sonrasında içe giren kısım tekrar kırılacaktır.
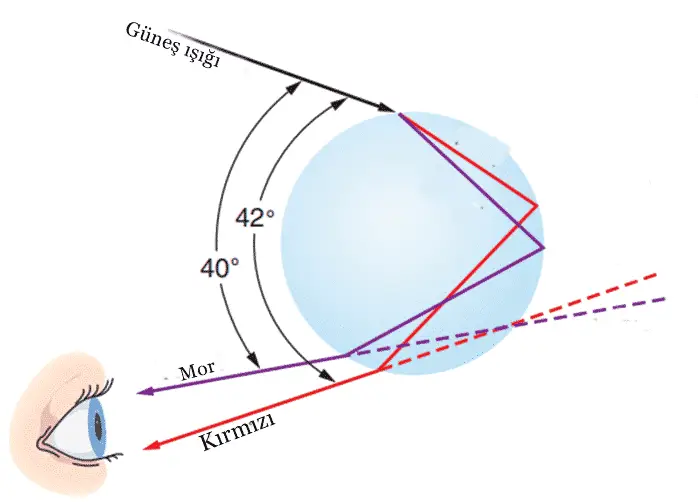
Bu ikinci geri yansıma esnasında da elbette bir kere daha kırılacaktır. Bu kırılmalarda bir ortamdan diğerine geçerken bir ışığın yavaşlamasının bir sonucudur. Bunu şu şekilde de düşünebilirsiniz. Bir alışveriş arabasını asfalt yoldan çimenlerin üzerine belli bir açıyla ittiğinizi düşünün. İlk etapta arabanız yön değiştirecektir. Çünkü arabanın çimenlere ilk çarpan tarafı ilk etapta yavaşlayacaktır.
Güneş’ten gelen ışık dünyamıza doğru yol alırken tüm frekanslar aynı hızda yani saniyede yaklaşık 300.000 km yol alır. Bu ışık suyla temas ettiği zaman frekanslar değişmez. Ancak hızı frekansa bağlı olarak bir miktar değişecektir. Farklı frekanslardaki ışık, farklı miktarlarda kırılır. Bunun nedeni, suyun atomik yapısının farklı frekanslardaki dalgalarla farklı şekilde etkileşime girmesidir. Kırılma indisi, bir ışını bir ortamdan diğerine, örneğin havadan suya geçerken ne kadar kırıldığının ölçüsüdür.
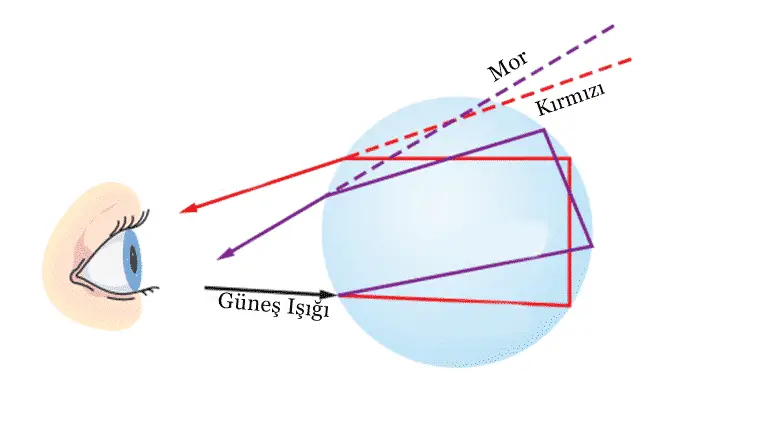
Hangi renklerin oluşacağı ise kırılma açısı tarafından ışınların dalga boyuna bağlı olarak belirlenir. Kırılmalar ve yansıma nedeniyle, bileşen renkleri yerdeki bir gözlemci için 40 ° ila 42 ° arasında dar bir aralıktadır. Bu nedenle, yedi renk yalnızca Güneş, dağılan ışık bu açılardan size yansıyacak şekilde konumlandığı zamanlarda görülür.
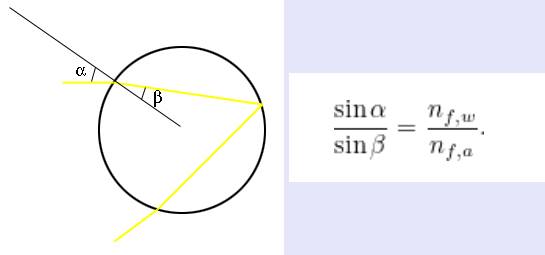
Ayrıca görselde noktalı çizgilere bakarsanız kırmızı rengin mor rengin üzerinde olduğunu fark edeceksiniz. Bu nedenle gökkuşağının en dışında kırmızı renk, en içinde de mor renk algılanır. Gökkuşağı üzerindeki renkler dalga boylarına göre en uzundan en kısaya doğru sıralıdır. Bu sıralama kırmızı, turuncu, sarı, yeşil, mavi ve mor rengi biçimindedir. Damlacık içine girerken farklı frekanslardaki ışığın ne kadar büküldüğü ise Snell yasasıyla açıklanır.
Aynı Anda Kaç Gökkuşağı Görebiliriz?
Bazen koşullar, güneş ışığının su damlacıklarında iki kez iç yansımaya maruz kalacağı şekildedir. Bu durumda aynı anda iki gökkuşağı görebiliriz. Bunların merkezleri aynı, ancak çapları farklıdır. Yani biri içte, öteki dıştadır.
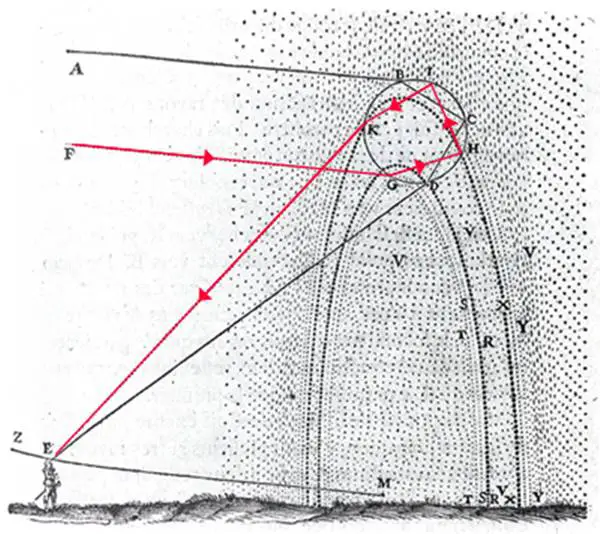
Dıştaki gökkuşağı içtekine, yani asıl kuşağa göre daha sönük olur. Çok parlak bir gökkuşağının çevresinde nadiren 3. hatta 4. bir gökkuşağı da görebiliriz. 2. gökkuşağının renk sıralaması ilkinin tersinedir. Gökkuşağının şeklini ilk kez açıklayan, hem birincil hem de ikincil gökkuşağını gösteren René Descartes’ın orijinal çizimini aşağıda görebilirsiniz. İkincil gökkuşağına karşılık gelen çift yansıma kırmızıyla çizilmiştir.
Gökkuşağının Gerçek Şekli Nasıldır?
Gökkuşakları aslında tam bir çember şeklinde oluşur. Uçakta yolculuk yapanlar bazen bu dairesel gökkuşaklarına şahit olabilirler. Ancak yerdeki izleyiciler yalnızca ufuk çizgisinin üzerindeki yağmur damlalarının yansıttığı ışığı görebilir. Yüksek bir dağın tepesine çıkıp gökkuşağı görme şansı yakalarsanız o zaman gerçek şeklini görebilirsiniz.

Bu arada son olarak hatırlatalım. Sadece arkanız güneşe dönük dururken bir gökkuşağı görürsünüz. Gökkuşağı ışınlarını yakalamanın tek yolu budur. Ayrıca, gökkuşağının geometrisi, gördüğünüz herhangi bir gökkuşağının yalnızca size ait olduğunu gösterir. Yanınızda duran kişi ne görürse görsün, gördükleri farklı bir su damlacıkları grubundan gelecektir ve bu nedenle farklı bir gökkuşağı olacaktır.
Bahar ayları, gökkuşağı görmek için en uygun mevsim. Şansınızın bol olması dileğimizle. Ayrıca merak ederseniz: Ufuk Çizgisi Ne Kadar Uzaktadır? Ne Kadar Uzağı Görebiliriz?
Kaynaklar ve İleri okumalar:
- Maths behind the rainbow; Yayınlanma tarihi: 21 Ekim 2021; Kaynak site: Plus Maths. Bağlantı: Maths behind the rainbow;
- How Are Rainbows Formed? The Science Behind the Colors. Yayınlanma tarihi: 23 Temmuz 2023. Kaynak site: How Stuff Works. Bağlantı: How Are Rainbows Formed? The Science Behind the Colors
- Rainbow; https://www.nationalgeographic.org/
- Here’s why rainbows have a curved or arcing shape. Yayınlanma tarihi: 29 Temmuz 2023. Kaynak site: Earth. Bağlantı: Here’s why rainbows have a curved or arcing shape
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





