Çin bilimkurgu yazımı son on yılda küresel beğenide giderek daha çok öne çıkmaya başladı. Bunda yazar Liu Cixin tarafından kaleme alınan Üç Cisim Problemi isimli kitabının (2006) önemli bir katkısı vardı.

Tarihi ve kültürel hikaye anlatımının benzersiz karışımı sayesinde Liu’nun üçlemesinin büyüsüne pek çok okuyucu kapıldı. Netflix’in “Üç Cisim Problemi” dizisi, kitabı ekranlara taşıyınca da bir çok kişinin aklına aynı soru geldi. Üç cisim problemi gerçek hayatta nedir?
Dizi, teknolojik açıdan üstün bir uygarlık, ekolojik yıkım ve çatışmalarla boğuşan bir gezegen olan Dünya’yı işgal ederse, insanlık nasıl tepki vermeli? İnsanlık kurtarılmaya değer mi? Kendimizi kurtarmak mümkün mü? gibi soruların etrafında dönüyor.

Trisolaryalılar, Trisolaris isimli verilen bir gezegende yaşıyor ve bu gezegen üç güneşin etkisi altında bulunuyor. Bunun sonucunda da Trisolaryalılar üç cisim probleminin yarattığı sorunlarla boğuşmak zorunda kalıyor. Sorunların başında da, gezegenin birkaç dakika içinde şiddetli soğuktan yakıcı sıcağa geçmesi yer alıyor. İnsanlıktan umudunu kesen astrofizikçi Ye Wenjie’nin onları dünyaya müdahale etmeye yönlendirmesiyle de dizi, insan uygarlığını korumaya yönelik karmaşık çabaları ekranlara yansıyor.
Fizikte Üç Cisim Problemi Nedir?
Üç cisim problemi, fizik ve matematikte zorlu bir bilmecedir. Bir yıldızın etrafında dönen bir gezegen mi? Sorun değil. Bir yıldızın etrafında dönen iki veya daha fazla gezegen mi var? İşte bu ciddi bir sorundur.
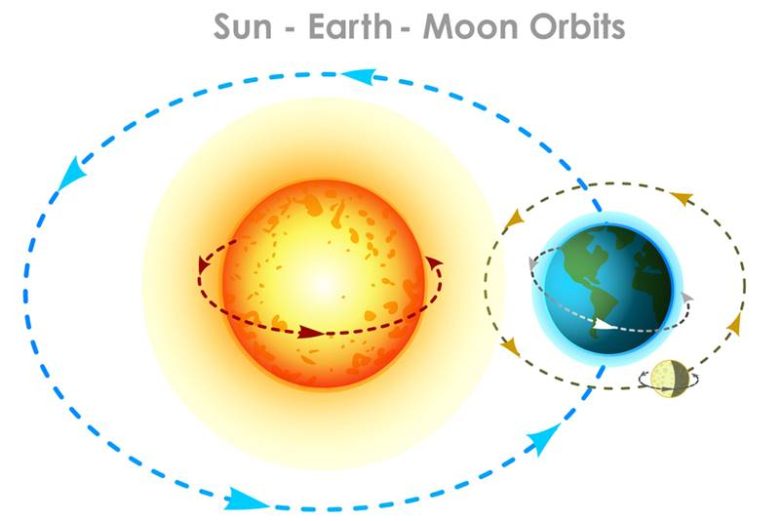
Isaac Newton, 1660’larda Dünya-ay sistemi için iki cisim problemini çözmüştü. Günümüzde bu sayede ayın yörüngesini olağanüstü bir hassasiyetle tahmin edebiliyoruz. Matematikçiler o zamandan bu yana üç cisim probleminin çözümleri üzerinde çalışıyorlar. Ancak üç cisim probleminin genel bir çözümü yok. Yani üç cismin nasıl hareket edeceğine dair bir formül yazamıyoruz. Yapabileceğimiz tek şey çok sayıda özel durum bulmaktan öteye geçemiyor.
Üç cisim problemi daha da genel haliyle n-cisim problemi nedeniyle, Güneş Sistemindeki gezegenler için dahi, yörüngelerinin her zaman bugün olduğu şekilde kalmaması ve gerçek anlamda tahmin edilemeyecek yollara sapması ihtimali mevcuttur.

Üç Cisim Problemini Çözmek Neden Zordur?
Problemin çözümünde amaç, herhangi bir anda üç cismin konum ve momentum değerini verecek bir denkleme ulaşmaktır. Ancak her bir cismin hareketi diğer ikisinin hareketine bağlıdır ve sistemin kütle merkezi sürekli konum değiştirir. Bu nedenle cisimlerin ilk konumlarını ve momentumlarını tam bir doğrulukla ölçmek imkansızdır.
Ayrıca n, 3 veya daha büyük olduğunda, cisimlerin yollarının genellikle korkunç derecede karmaşık hale geldiği görülmektedir. Üç cisim probleminin çözümünün olmayışı matematikçilerin insani yetersizliğinden daha çok, bu eksikliğin matematiğin yasalarının içine gömülü olmasından kaynaklanmaktadır.
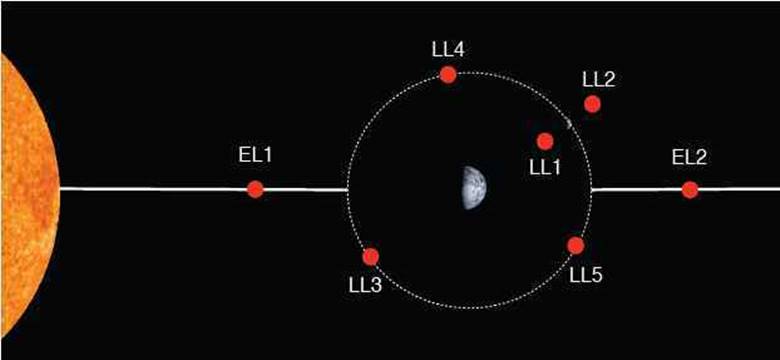
Joseph-Louis Lagrange, üç cismi aynı düzlemde hareket edecek şekilde kısıtlarsak ve bunlardan birinin kütlesinin ihmal edilebilecek kadar küçük olduğunu varsayarsak, üç cisim problemine en azından bazı çözümleri olduğunu gösterdi. Çözümlerinde, üç cisim uyum içinde hareket etti. Ayrıca her zaman birbirine göre konumlarını korudu.
İki cisimli bir sistem düşünürsek, o zaman üçüncü bir küçük cismin bulunabileceği noktalar şimdi onun onuruna Lagrange noktaları olarak bilinmektedir. Muhtemel Lagrange insan yapımı bir uzay aracının kendi adını taşıyan bu noktalara “park etmesini” hayal etmemişti. Ancak bu noktalar günümüzde tam olarak bu amaçla kullanılmaktadırlar.
Lagrange noktaları üç cisim problemine tam olarak cevap vermez. Eğer hepsi büyük ve oldukça yakın olan üç nesneden oluşan bir sistemimiz varsa, onların hareketleri kaotiktir. Bu, kısa bir süre içinde onlara ne olduğunu öğrenebilmemize rağmen, uzun bir süre içinde bunun tahmin edilemez hale gelmesi anlamına gelir.
Üç Cisim Problemini Çözme Girişimleri
Fiziğin güzel yanlarından biri deterministik olmasıdır. Yani bir sistemin tüm özelliklerini biliyorsanız ve fizik yasalarını biliyorsanız, o zaman geleceği mükemmel bir şekilde tahmin etmek mümkündür. Ancak doğanın hem deterministik hem de öngörülemez olabileceğini 1800’lü yıllarda öğrendik.

1889’da İsveç Kralı II. Oscar, soruya genel bir çözüm sağlayacak kişilere bir ödül vaat etmişti. Sonunda, Fransız matematikçi Henri Poincaré problemi çözmeden ödülü kazanacaktı. Ancak kendisi sorunu çözmek yerine, sorunun çözülememesinin nedenlerini açıklayacaktı. Vurguladığı en önemli nedenlerden biri de sistemin başlangıcındaki küçük farklılıkların sonunda büyük farklılıklara yol açacağıydı. Bu kaotik evren fikrinin başlangıcıydı.
Birbirleri etrafındaki bir yörüngede bulunan üç cisim için, tekrar eden adımlar halinde hesaplamayı yapmak mümkündür. En başta, cisimlerden birinin hareketsiz olduğunu varsayıp diğer ikisinin kendi yörüngelerinde kısa bir mesafeyi nasıl kat ettiklerini hesaplarız. Daha sonraysa bu yeni pozisyonlardan başlayarak diğer bir cisim hareketsiz tutulurken öteki ikisinin hareketini hesaplar ve bunu üçüncü cisim için de tekrar etmek yoluyla bir sonuç elde ederiz.
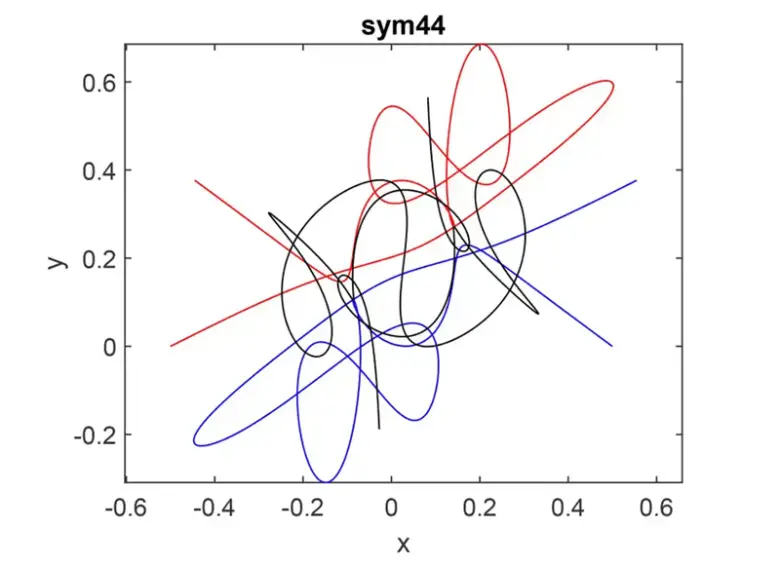
Ancak yine de elde edeceğimiz sonuçlar mükemmel olmayacaktır. Çünkü bu üç cisim birlikte ve aynı anda hareket etmektedir. Gelişen teknolojinin sayesinde matematikçiler olası çeşitli yörüngeler hesaplayabilir. Ancak bunlar yukarda da gördüğünüz gibi çarpık ve karmaşık görünecektir.
Sonuç olarak
Üç cisim sistemleri evrende oldukça yaygındır. Sonucunda birden fazla gezegene sahip çok sayıda yıldız sistemi, hatta birbirinin etrafında dönen birden fazla yıldız vardır. Trisolaryalıların yaşadığı kurgusal gezegen kaotik bir sistemi temsil ediyordu. Fizik ders kitaplarında yalnızca bir yıldız ve yörüngede dönen bir dünyadan oluşan mükemmel şekilde yalıtılmış bir sisteme sahip olabilirsiniz, ancak gerçek Evren bu tür basitlikten kaçınır.
Kaynaklar ve İleri Okumalar:
- Mathematical mysteries: the three body problem; Yayınlanma Tarihi: 1 Eylül 1998; Kaynak site: Plus Math. Bağlantı: Mathematical mysteries: the three body problem/
- We Just Got 12,000 New Solutions to The Infamous Three-Body Problem. Yayınlanma tarihi: 23 Temmuz 2023. Bağlantı: https://www.sciencealert.com/
- The Three-Body Problem. Liu Cixin’s extraterrestrial novel is a heady blend of politics, ethics, physics and Chinese history. Yayınlanma tarihi: 8 Mart 2024. Kaynak site: Conversation. Bağlantı: The Three-Body Problem. Liu Cixin’s extraterrestrial novel is a heady blend of politics, ethics, physics and Chinese history
Matematiksel










