Bilim haberlerini takip ediyorsanız James Webb Uzay Teleskobu ile adı anılan L2’yi ya da, L4’te gizlenen bir asteroidi duymuş olmanız mümkündür. Bu kısaltmalar Lagrange noktalarına aittir. Lagrange noktaları aslında toplam beş tanedir. Bu nedenle noktalar L1, L2, L3, L4 ve L5 gibi isimler almaktadır. Peki ama Lagrange noktaları nedir?

Öncelikle çok kısa bir giriş yapalım. 15. yüzyılın başında Copernicus, gezegenlerin Güneş’in etrafında döndüğüne dair devrim niteliğinde bir fikir ortaya attı. Bu yeni dünya görüşü bazı çevrelerde düşmanlıkla karşılansa da, yaklaşık bir asır sonra Kepler ve Galileo da dahil olmak üzere önemli bilim insanları bunu kabul ettiler. Ama gezegenler tam olarak nasıl hareket ediyordu?
Bu soruya matematiksel olarak kesin bir cevap bulmak yaklaşık 150 yıl sonra, Isaac Newton’un parlak zekası sonucunda olacaktı. Birbirinin etrafında dönen ve her biri diğerine çekim kuvveti uygulayan iki büyük cismin olduğunu düşündü. Sonrasında yeni geliştirdiği kalkülüs yardımıyla ilgili denklemleri çözdü sonucun bir elips olduğunu doğruladı. Sonucunda Newton, “iki cisim probleminin” tam olarak çözülebileceğini de göstermişti. Bir sonraki soru ise “üç cisim problemi” olacaktı.
Ancak bu soru çözmek çok daha zordu. Bunun nedeni üç cismin de değişen yerçekimi kuvvetinin çok karmaşık davranışlar üretmesiydi. Aslında tam olarak farkında olmadan, o zamanki matematikçiler kaosun ilk örneklerinden birine rastlamışlardı.
Çok geçmeden üç cisim probleminin kolayca çözülemeyeceğini anlayacaklardı. Çözümü için bazı kısıtlamalara ihtiyaç vardı. Bu üç kütleden bir tanesinin kütlesini ihmal etmek gerekliydi. Yani bu üç cisim Dünya, Ay ve yörüngede yer alan bir toz tanesi olduğu zamanlarda bir çözüm bulmak mümkün olacaktı.
Lagrange Noktaları Nasıl Keşfedildi?

İki büyük matematikçi, Euler ve Lagrange, 1772’de Paris Bilimler Akademisi tarafından bu probleme çözümlerinden dolayı verilen bir ödülü paylaştılar. Buldukları çözüm uzayda Dünya-Ay gibi ikili sistemlerin için de özel bölgelerin var olduğunu gösterdi. Bu bölgelere yerleşen bir uzay gemisi, diğer ikisine göre konumu koruyarak yörüngede dönebilirdi.
Euler bu tür üç konum buldu. Ancak Lagrange’ın analizi daha kapsamlıydı ve daha az belirgin olan iki noktayı daha keşfetti. Bu nedenle de bu noktalar günümüzde onun adını taşıyor ve Lagrange noktaları olarak isimlendiriliyor.
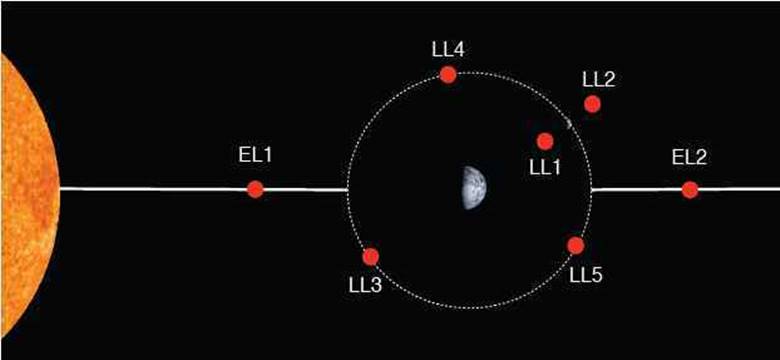
Lagrange Noktaları Nerededir?
Aşağıdaki şema, Dünya’nın çevresindeki Lagrange noktalarını gösteriyor. İlk üç Lunar Lagrange noktası (L1, L2 ve L3) Dünya ile Ay’ı birleştiren çizgi üzerinde yer alır. L4 ve L5’in her biri bir eşkenar üçgenin üçüncü noktasını oluşturur. Bu nedenle Ay Dünya’yı çevrelerken daima 60° önünde ve arkasında durur.
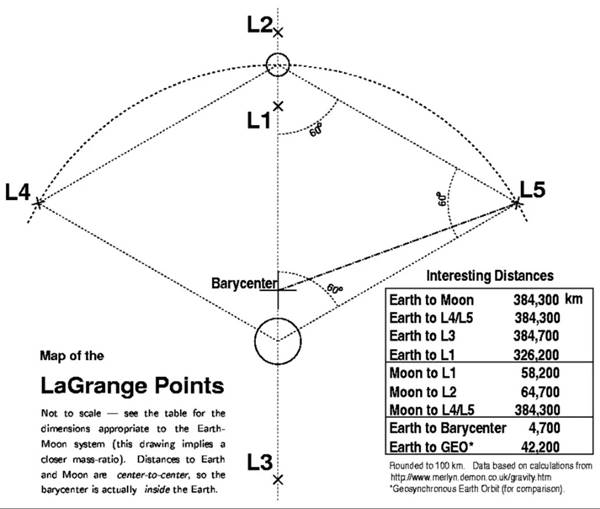
Beş Lagrange noktasından herhangi birinde, bir uzay gemisi az bir çabayla iki büyük cisme göre sabit bir konumu korur. Bu nedenle uzun süreli uzay görevleri için mükemmeldirler. L1 noktası, Güneş’in sınırsız bir görüntüsünü sunduğu için (SOHO) tarafından kullanılıyor. Kendisi sürekli olarak Güneş’i gözlemliyor ve aldığı veriyi kolaylıkla Dünya’ya gönderiyor.
James Webb, Dünya’dan 1,5 milyon km ötede bulunan L2 noktasında yer almaktadır. Aynı zamanda Herschel, Planck ve GAIA uyduları da bu noktada bulunur. L3 noktası ise Dünya’dan bakış doğrultumuza göre sürekli olarak Güneş’in arkasında olduğu için, Dünya ile iletişim sorunu dikkate alındığında, uzay aracı göndermenin ideal olmadığı bir yerdir.
L1, L2 ve L3 Noktaları Kararsız Yapıdadır
Bazı Lagrange noktalarının etrafındaki kesin dinamikler, Euler ve Lagrange’ın tahmin edebileceğinden çok daha karmaşıktır. Bunu anlamak, modern dinamik sistemler teorisinin tam gücünü gerektirir. İki nokta L4 ve L5 “kararlı denge” dir. Yani L4 ve L5 noktalarındaki uzay araçlarına veya uydulara sürekli olarak yörünge düzeltmesi yapmak gerekmez.
Bununla birlikte, ilk üç Lagrange noktası L1, L2 ve L3 “kararsız dengelerdir”. Bu nedenle, o noktalara gönderilen uzay araçlarına veya uydulara birkaç haftada bir yörünge düzeltmesi yapılmalıdır.

Gördüğümüz gibi, matematik ile analiz, yalnızca iki büyük cismi tanımlayan denklemlere kesin çözümler bulabilir. Güneş sistemimizdeki dokuz gezegenin tümünün hareketleri hakkında herhangi bir şeyi nasıl tahmin edebiliriz?
Lagrange Noktaları Gezegenler Arası Bir Otoban Gibi Kullanılabilir mi?
Güneş sisteminin yerçekimi alanı içinde farklı konumlar arasında hareket etmek enerji gerektirir. Hava sürtünmesi olmamasına rağmen, güneş sisteminde iki konum arasında hareket etmek, genellikle bir hız değişikliği sağlamak için bir roket patlaması veya bilindiği adıyla “delta V” gerektirir. Yerden alçak bir Dünya yörüngesine (LEO) ulaşmak için gereken delta V, 9,7 km/s’dir. Bir uzay aracını LEO’dan L1 noktasına göndermek için delta V 3,15 km/s’dir (yerçekimi kuvveti mesafeyle azaldığı için çok daha azdır).
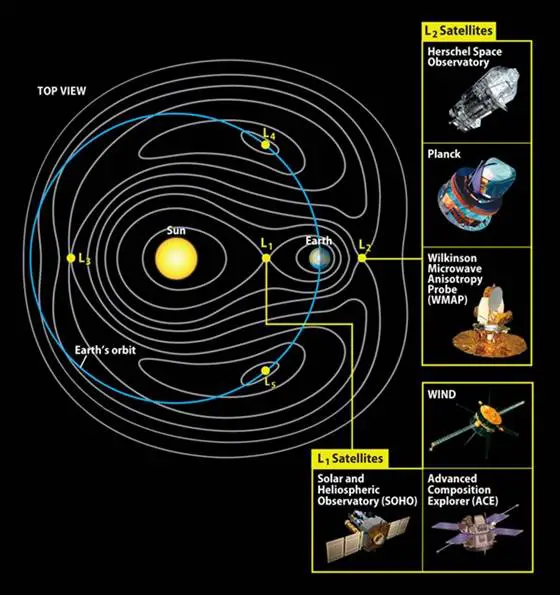
L1’den L2’ye bir buçuk milyon kilometrelik yolculuk için gereken delta V ise sadece 0,014 km/s’dir. Bu da uzay araştırmaları için harika bir fırsattır. Peki gezegenler arası bu kısa yollardan başka var mı? Sonucunda böyle bir ağ olsa güneş sistemimizi kolayca ve çok daha kısa sürede dolaşabilirdik.
Böyle bir ağın keşfinin temelleri, 19. yüzyılın sonlarında efsanevi matematikçi Jules-Henri Poincaré tarafından atıldı. Poincaré üç cisim problemi üzerinde çalıştı. Can alıcı gözlemi, kararsız Lagrange noktalarının yakınındaki parçacıkların yörüngelerini tam olarak tahmin etmenin imkansız olmasına rağmen, benzer şekilde davranan yörünge ailelerini ayırabileceğinizdi.
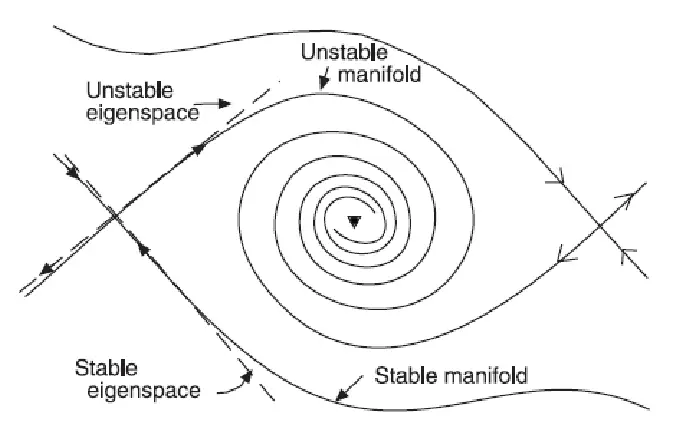
Bu benzer yörüngeler birlikte bir ağ yapısı oluşturur. Bu ağı manifoldlar yardımı ile inceleyebiliriz. Manifold bizlere metrikten bağımsız ve hatta topolojiden bağımsız geometri yapma olanağı sağlar. Şimdi yukardaki görselde gördüğünüz gibi unstable yani “kararsız manifold” u giden yol “stabil manifold” yani kararlı manifoldu gelen bir yol gibi düşünün. Aslında her karasız Lagrange noktasının yakınında, birbirinin etrafında çok karmaşık bir şekilde dolanan, ancak nihayetinde çılgınca farklı yönlere giden çok sayıda böyle yollar vardır.
1980’lere kadar uzay yolculuğu için manifoldlardan yararlanma fikri ciddi olarak dikkate alınmamıştı. Ancak son birkaç yılda, NASA matematikçisi Martin Lo ve ekibi bu fikir etrafında ayrıntılı bir teori geliştirdiler. Artan bilgi işlem gücüyle, bu bilim insanları gerçekten de bu tür düşük enerjili yollar buldular.
Gezegenler Arası Otoyol Fikri Sadece Bir Hayal Değildir
Dünyanın Lagrange noktaları, bu minimum enerji yörüngeleri ile Mars veya Satürn’ünkilerle bağlantılıdır. Jüpiter, birçok ayının her biri ile ilişkili Lagrange noktalarına sahiptir. Ayrıca hepsi, Jüpiter-Güneş Lagrange noktaları aracılığıyla Dünya sistemine bağlanan, birbirine bağlı bir ağda birleştirilmiştir. Sonucunda bu rotalarda seyahat eden uzay aracı, hedeflerine verimli bir şekilde ulaşabilecektir. Şimdilik teoride de olsa bu fikir etkileyicidir.
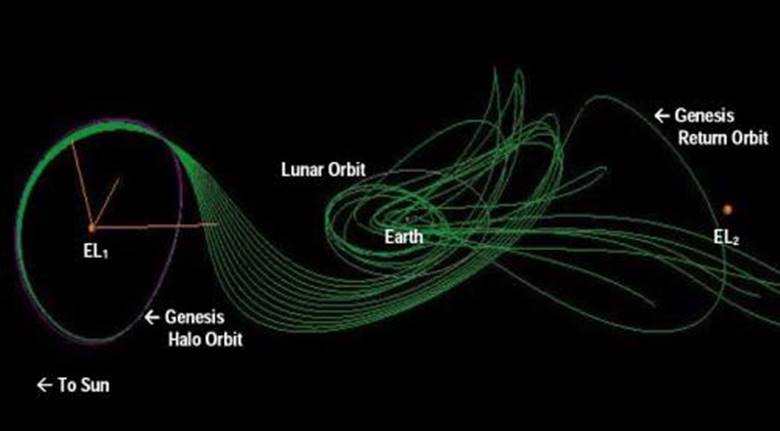
Sonucunda bu ağ, güneş sistemi kadar eskidir ve tamamen görünmezdir. Ancak matematiğin gücü olmasaydı keşfedilmeden kalırdı. Bu düşük enerjili yörünge sistemini keşfeden matematikçiler buna Gezegenler Arası Otoyol veya IPS adını verdiler.
Şu ana kadar okuduklarınız size bir bilim kurgu gibi geldiyse aslında yanılıyorsunuz. Bu fikir aslında bir kaç defa kullanıldı. Örneğin “Genesis”, 2001 yılında Martin Lo yönetiminde başlatılan bir araştırmaydı. Görevi, Güneş rüzgarından örnekler toplamaktı. Tüm görev, Dünya’ya kesin varış zamanına kadar, kaos matematiği ve bilgisayarlar kullanılarak yıllar öncesinden hesaplanmıştı.
Tüm bunlar Euler ve Lagrange’ın dahi beyinleri sayesinde oldu. Şimdi kendi çığır açan yöntemlerimizi kullanıyor, güneş sisteminin içinden uzanan görünmez tünellerde ilk adımlarımızı atıyoruz.
Kaynaklar ve ileri okumalar
- Lagrange and the Interplanetary Superhighway; yayınlanma tarihi: 1 Eylül 2005; https://plus.maths.org/
- Interplanetary Superhighway Makes Space Travel Simpler. Yayınlanma tarihi: 7 Temmuz 2012; Bağlantı: https://www.nasa.gov/
- Fun Places To Hang Out In Space: What Are Lagrange Points? Yayınlanma tarihi: 9 Şubat 2022; Bağlantı: https://www.scienceabc.com/
Matematiksel



