Çalışmalarıyla evrenin yapısının tarihteki ilk matematiksel modelini sunan Eudoxus, Archimedes’den Öklid’e, Aristoteles’ten Kepler ve Copernicus’a kadar bilim dünyasını etkiledi. Hatta kimilerine göre de Eudoxus, Antik Çağın en büyük matematikçisidir. Arşimet‘e atfedilen π‘yi hesaplama yönteminin, aslında Eudoxus’a ait olduğunu söyleyenler de vardır. Bu nedenle kendisini tanımamız gerekir.
Muğla’nın Datça ilçesine bağlı Knidos’ta M.Ö. 408 yılında dünyaya gelen Eudoxus, Platon’un öğrencisidir. Genç yaşlardan itibaren Platon’un Akademisi’nde matematikçi ve askeri idareci olan hocası Arkitas ile bilimsel çalışmalarına ağırlık verir. Eudoxus yaşadığı zaman boyunca Yunan matematiğini zirveye taşır.
Çok yönlü bir bilim insanı olan Eudoxus, felsefe, teoloji, matematik, coğrafya ve hukuk alanında kendisini geliştirir. Ayrıca Sicilya’da tıp eğitimi görür ve doktorluk mesleğini de icra eder. Ders verme amacıyla Mısır’a da giden Eudoxus, burada astronomik gözlemler yapma fırsatı yakalar.
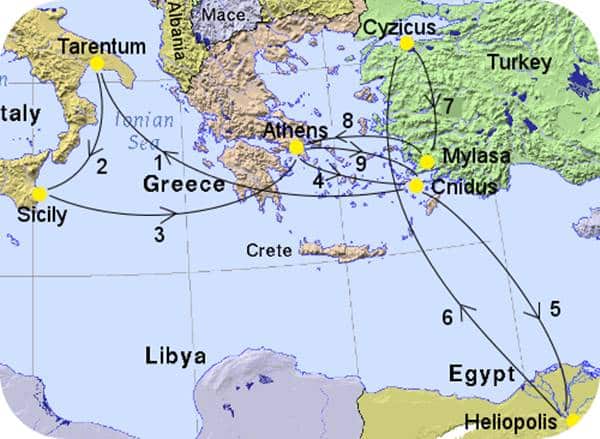
Devamında da M.Ö. 363 – 357 yılları civarında Cyzicus’da bir astronomi okulu kurar. Öğrencileri ile M.Ö. 348 yılında Atina’ya geri döner. Sonrasında da Platon’un Akademisi’ne resmi olarak katılmasa bile orada ders vermeye devam eder. Platon’un ölümüyle astronomi çalışmalarına ağırlık verir. Evli ve üç kız çocuğu babası olan Eudoxus, M.Ö. 355 yılında vefat eder. Ölmeden önce hukuk alanında da çalıştığı bilinmektedir.
Eudoxus’un Matematiğe Katkıları Nelerdir?
İrrasyonel sayılar (kesir olarak ifade edilemeyen sayılar) mantığını ileriye taşıyarak sayılar teorisine kazandırdığı çalışmalarıyla Öklid’in geometri anlayışını da etkiler. Knidos’lu Eudoxus, Pisagor’un yolunda gitmeyerek sayı kavramı yerine onun geometrik karşılığı olan “uzunluk” kavramını kullandı. (Detaylar için bu yazımıza göz atınız. Her şey Sayı mı Yoksa Geometri mi? Pisagor ve Eudoxus)
Çalışmalarından biri olan Eşit Oranlar Teorisi, oran ve orantı konusunun gelişimine katkıda bulunur. Bu teorisi Öklid’in Elementler Kitabının V. ve VI. Cildinin; diğer bir çalışması Ölçülemeyen Büyükler Teorisi (ortak bir ölçütü olmayan büyüklükler) ile de aynı kitabın X. ve XII. Cildinin temel kaynağı olur.
Öklid’in beşinci kitabı Eudoxus’un oranlar kuramını anlatır. 19. yüzyılda Richard Dedekind gelip rasyonel sayılardan reel sayıları elde etmenin başka bir yolunu gösterene kadar binlerce yıl Eudoxus’un yak- laşımıyla sayıları kavradık.
Tüketme Yöntemi Nedir?
Kendisi altın oran konusuna çalışır. Ayrıca Tüketme Yöntemi adını verdiği teorisini geliştirir. Bu yöntemle bir doğrunun uzunluğunun kendi içinde nasıl bölünebileceğinin hesaplamalarını yapar. Piramitler ve konilerin, eş tabanlı ve eş yüksekli prizma ve silindirlerin hacminin üçte birine eşit olduğunu kanıtlamak için bu yöntemden yararlanır.
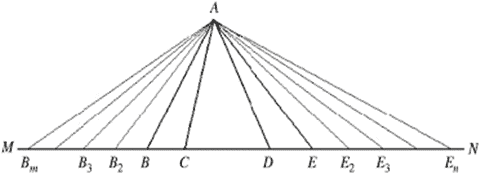
Eğrilerle sınırlandırılan cisimlerin alan ve hacim hesaplarını bulur. Bu hesaplamalar, Öklid’in Elementler Kitabının VII. Cildinde yer alır. Tüketme Yöntemi, İntegral kavramının Antik Çağ’daki karşılığıdır denebilir. Eudoxus bu yöntemi ustaca kullanarak birçok sonucu ispatlamıştır. Bunlardan bazıları aşağıdaki gibidir.
- Dairenin alanı, yarıçapının karesi ile aynı ölçüdedir (yani orantılıdır).
- Kürenin hacmi, yarıçapının küpü ile aynı ölçüdedir (orantılıdır.)
- Piramidin hacmi, tabanı üzerine kurulmuş aynı yükseklikteki bir prizmanın hacminin üçte biridir.
- Koninin hacmi, tabanı üzerine kurulmuş aynı yükseklikteki silindirin üçte biridir.
Günümüzde Arşimet Aksiyomu olarak bilinen önerme, aslında kendisinin oluşturduğu orantı kuramına bağlı olarak Arşimet tarafından geliştirilir. ( Detaylar için: Arşimet’in Tüketme Yöntemi İle Bir Parabolün Alanını Hesaplaması)
Bu aksiyoma göre; 2 doğru parçası veya 2 sayı verildiğinde, en küçük doğru parçası ya da sayının, her zaman en büyük parçayı ya da sayıyı kapsayan bir tam katı vardır. Sonucunda bu aksiyom matematik tarihi boyunca matematikçilerin çalışma konularından biri olur.
Astronomi Bilimine Katkıları
Evrenin düzenini belirlemek için gözlemlerin, matematiksel astronomi çalışmalarının temeli olması gerektiğini belirten ilk teorisyen olan Eudoxus, “Eş Merkezi Küreler Teorisi” ile bilimsel astronominin öncüsü olur. Eudoxus’un astronomi hakkında 5 temel ilkesi şöyledir:
- Dünya, evrenin merkezidir.
- Bütün gök hareketleri daireseldir.
- Bütün göksel hareketler düzenlidir.
- Herhangi bir gök hareketinin yolunun merkezi, hareketinin merkezi ile aynıdır.
- Tüm göksel hareketin merkezi, evrenin merkezi ile aynıdır.
Antik Çağda bilinen 5 gezegen Merkür, Venüs, Mars, Jüpiter ve Satürn’ün geometrik modellemesi üzerine çalışır.
Bu teorisinde, “bütün gök hareketleri daireseldir” prensibinden yola çıkar. Amacı, anlaşılması zor olan gök cisimlerinin hareketlerinin periyodik olarak nasıl gerçekleştiğini bulmaktır. Gezegenlerin hareketlerinin düzensiz, yıldızların hareketlerinin periyodik bir düzen içerdiğini fark eder.
Eudoxus’da küreler yardımıyla bu hareketlerin düzenini anlamaya çalışır. Eş Merkezi Küreler Teorisi ile Güneş saatini ve bir yılın uzunluğunun 365 gün 6 saat olduğunu açıklayan ilk bilim insanı olur.
Eş Merkezi Küreler Teorisi Nedir?
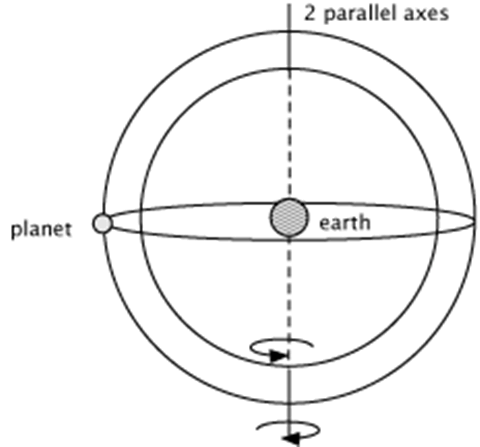
Evreni; dönme eksenleri farklı eğimli ve iç içe geçmiş küreler biçiminde, ortak bir merkeze sahip olarak betimler. Yani her iç içe küre bir sonraki küreye bağlanır. Böylece merkezi küre diğer kürelerin dönüş hareketini de belirler.
Buna karşın her küre bağımsız olarak kendi ekseni etrafında da döner. Bu tasarımdaki tek koşul, “tüm göksel hareketlerin düzenli olması” prensibidir. Gezegenlerin çapları ve dönme eksenleri farklıdır. Fakat bir kürenin ekseni, kendi eksenine sahip başka bir kürenin dönmesine bağlı olduğundan tek bir dairesel yörünge olarak değil, iki yörüngenin hareketlerinin bileşkesi olarak döndüklerini hesaplar.
Dünya hareketsiz bir biçimde en içtedir. Bu esnada küreler de içten dışa doğru Ay, Merkür, Venüs, Güneş, Mars, Jüpiter ve Satürn biçimindedir. En dıştaki kürede periyodik olarak hareketlerini 1 tam günde tamamlayan yıldızlar yer alır.
Gezegenlerin sahip olduğu 4 küreden ilki günlük hareketi, ikincisi periyodik hareketi, diğer iki küre ise duraklama ve gerileme hareketlerini açıklar. Son iki küre birbirine ters yörüngede hareket eder.
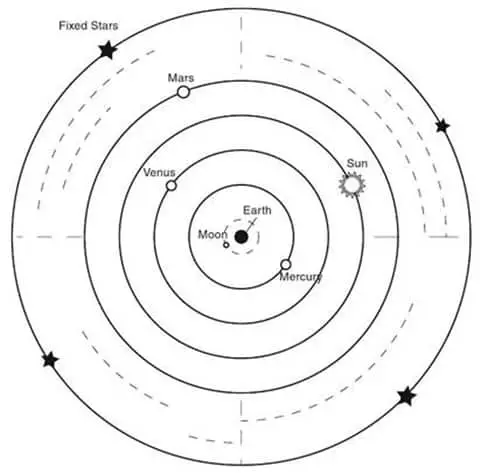
Eudoxus küreler teorisinde fiziksel değil matematiksel yaklaşım sergiler. Eudoxus’un tasarlamış olduğu gök cisimlerin küre şeklindeki gösterimi, modern astronominin kurucularından Kepler’e kadar (Alman Gökbilimci, 1571 – 1630) 2000 yıl boyunca astronomiye yön veren bir teori olur. Göz atmak isterseniz: Müzik İle Evrenin Uyumu: Kürelerin Müziği

Ne yazık ki Eudoxus’un çalışmalarından hiçbiri günümüze kadar ulaşamamıştır. Başarılarının bir kısmı, Aristoteles, Arşimet ve Hipparchus’un çalışmalarındaki alıntılar ve referanslar sayesinde öğrenilmiştir. Böyle bir adamın adını Ay’daki bir kratere vermek yetmezdi elbette. Ancak Mars’taki bir krater de Eudoxus’un adını taşır.
Kaynaklar ve ileri okumalar:
- Eudoxus of Cnidus. (Erişim Tarihi: 23.05.2020) https://web.calstatela.edu/
- Cnidus Eudoxus. (Erişim Tarihi: 23.05.2020);https://www.math.tamu.edu/
- Eudoxus of Cnidus. (Erişim Tarihi: 23.05.2020); tps://www.britannica.com
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel