Gökyüzündeki nesneler arasındaki mesafeleri yalnızca elleriniz ve parmaklarınızla ölçebileceğinizi biliyor muydunuz? Sonuçlar kişiden kişiye bir miktar değişse de yaklaşık olarak elde edeceğiniz sonuçlar gökyüzündeki bir cismin konumunu tarif ederken işinize yarayacaktır.

Dünyadaki iki nesne arasındaki mesafeleri ölçmeye yönelik geleneksel yöntemlerimiz, gök cisimleri arasındaki büyük mesafeleri ölçerken çok az anlam ifade eder. Bu nedenle gökbilimciler gök cisimleri arasındaki mesafeyi, Dünya üzerindeki gözlem noktasıyla yaptıkları açıya göre ölçerler. Bu nedenle de mesafeleri derece, dakika, saniye biçiminde ifade ederler. Bunu yapmak için de dünyayı aşağıda gördüğünüz gibi şeffaf bir kürenin içindeymiş gibi tanımlarlar. Bu durumda da karşımıza gökyüzü koordinat sistemi çıkar.
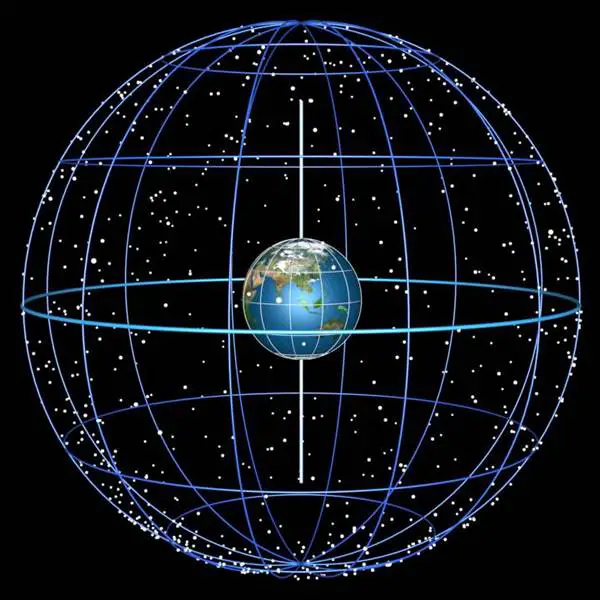
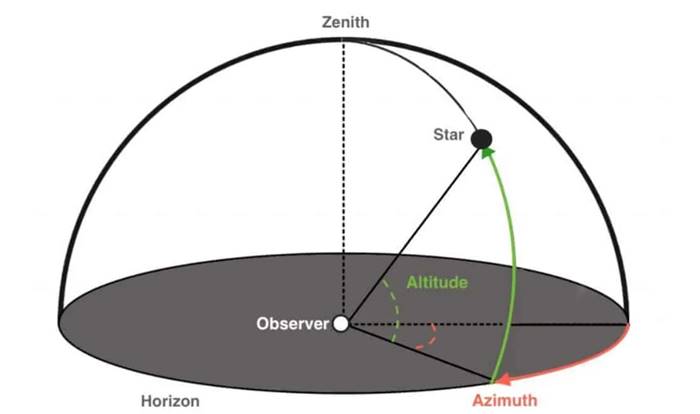
Herhangi bir anda bulunduğunuz yerden tam tepenizi yani başınızın ucundaki nokta başucu ( zenith) olarak tanımlanır. Başucunu 90 derece, ufku 0 derece olarak kabul edersek, karşımıza yeni bir koordinat sistemi çıkar. Buna gökyüzü koordinat sistemi denir. Bu koordinat sisteminde, bir gökcisminin konumu, iki koordinatla verilir. Bunlar yükselim ve meridyendir. Bir gökcisminin gözlemcinin bulunduğu yerde ufuktan yüksekliğine yükselim denir. Meridyen ise yerküredeki boylamlara benzer. Yükselim çizgilerini dik keser ve başlangıç meridyeni kuzey kutbundan geçer.
Büyük şeylerin uzaktayken küçük göründüğünü ve gözünüzün önünde tutarsanız küçük şeylerin büyük göründüğünü ilk fark ettiğinizde muhtemelen bir çocuktunuz. Eski Yunanlılar da bunu fark ettiler ve bir nesnenin görünen boyutu, gerçek boyutu ve mesafesinin nasıl ilişkili olduğunu keşfetmek için geometriyi kullandılar. Bunun için öncelikle küçük açı formülü adı verilen bir şeyi bilmeniz gerekiyor.
Küçük Açı Formülü Nedir?
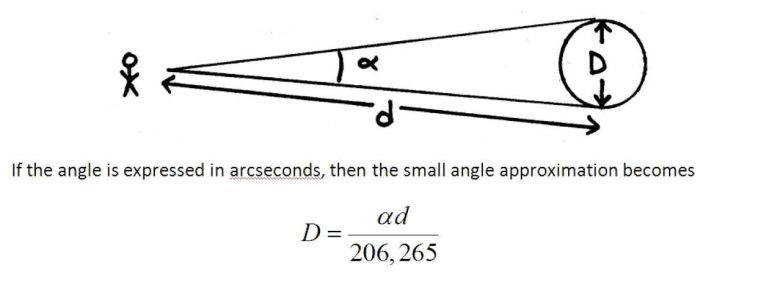
Küçük açı formülü, bir cismin uzaklığıyla görünür boyutu arasındaki ilişkiyi veren formüldür. Bir cismin görünür boyutu bir ucundan diğer ucuna ölçülen açı ile belirlenir. Formül yukarıdaki gibidir.
Gökyüzünü boydan boya çember biçimde 360 parçaya bölerseniz, her parça 1 derece olur. Daha küçük görünen boyutlar için, her dereceyi 60 yay dakikasına ve her bir yay dakikasını 60 yay saniyesine böleriz. Böylece bir derecede 3.600 yay saniyesi (60 × 60) olur. Küçük açı formülü yay saniyesi cinsinden ifade edilmektedir. Formülde gördüğünüz 206,265 sayısı da bu hesaplamanın bir sonucudur.
Gökyüzü ölçümleri için ellerimizi nasıl kullanacağız?
Yukarıda verdiğimiz teknik bilgilerden sonra işin pratik kısmına geçebiliriz. Amatör olarak astronomi ile ilgilenen biri için elleri aslında iyi bir ölçüm aracıdır. Öncelikle elinizi kol mesafesinde tutun ve bir gözünüzü kapatın. Elinizi bir yumruk yapın. Yumruğunuzun genişliği yaklaşık 10 derece olacaktır.

Bu noktada herkesin kolunun eşit olmadığını ve sonucun kişiden kişiye değişeceğini düşünebilirsiniz. Bu elbette doğrudur zaten elde ettiğimiz ölçümler yaklaşık sonuçlardır. Ancak insanların yumruklarının büyüklüğü genellikle kollarının uzunluğuyla orantılıdır. Bu nedenle küçük bir çocuğun kolu ve yumruğu ile yapacağı bir ölçüm, bir yetişkin ile aynı sonucu verecektir.
Bu, yumruğunuzun zıt uçlarında bulunan herhangi iki nesnenin birbirinden 10 derece uzakta olacağı anlamına gelir. Yumruğunuzu açın, serçe parmağınızı ve baş parmağınızı olabildiğince uzatın. Serçe parmağınızın ucu ve baş parmağınız arası yaklaşık 25 derece olur. İşaret parmağınız ile serçe parmağınız arasındaki uçtan uca açıklık ise yaklaşık 15 derecedir. Üç orta parmağınız yaklaşık 5 derece ve serçe parmağınız ise yaklaşık 1derece genişliğindedir.
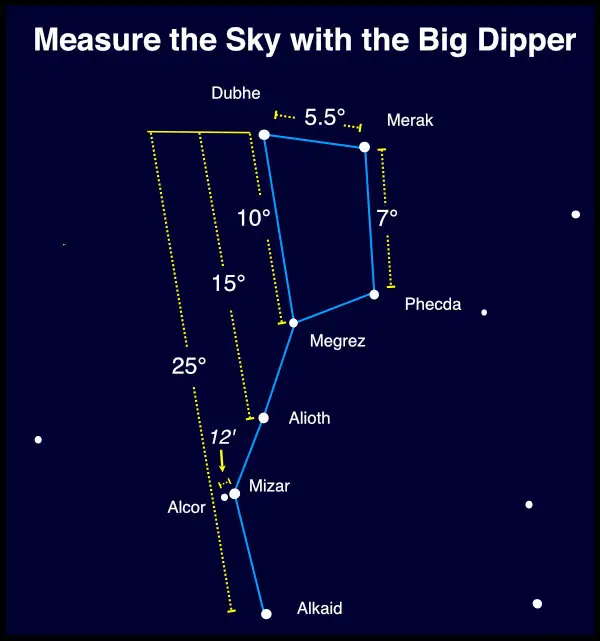
Büyük Ayı takımyıldızı içerisinde bulunan en parlak 7 yıldızın oluşturduğu kepçe veya cezve görünümde yıldız desenini anımsarsınız. Ellerinizi ile yaptığınız ölçümlerde, bu desen üzerinde pratik yapabilirsiniz. Büyük Kepçe’nin açısı mevsime ve gecenin saatine göre değişecektir, ancak Kuzey Yarımküre’nin çoğundan görmek kolaydır.
Ellerimiz İle Güneş Ve Ay’ın Büyüklüğünü Hesaplayalım
Dolunay sizce ne kadar büyüktür? Kaç derece olmasını beklersiniz? Çoğu insan abartsa da ölçüm sonucunda sizin de göreceğiniz gibi dolunayın çapı sadece 1/2 derecedir. Peki güneş? İçgüdüsel olarak boyutundan dolayı Güneş’in daha büyük olduğunu düşünüyor olmalısınız. Ancak Güneş ve Ay’ın kapladığı gökyüzü miktarının eşit, yani 1/2 derece olduğunu biliyoruz. Üstelik bunu bilmek için ölçüm yapmamıza da gerek yok. Tam güneş tutulmaları sırasında ayın geçici olarak güneşin tamamını kapattığını hatırlamanız yeterlidir.

Son olarak, ben astronomi ile ilgilenmiyorum. Bu benim ne işime yarayacak diyenlere bir hatırlatma. Güneş her saat başı 15 derecelik bir açıyla gökyüzünde hareket ediyormuş gibi gözükür. Bu da olası bir zor durum zamanında, gün batımına ne kadar süre kaldığını tahmin etmenize yardımcı olacaktır. Çünkü 15 derece yaklaşık olarak 1 saat yani 60 dakika anlamına gelecektir.

Bu durumda yapmanız gereken avucunuz size bakacak şekilde kolunuzu düz bir şekilde öne doğru uzatmaktır. Parmaklarınız bitişik olarak serçe parmağınızın alt kısmını ufuk çizgisine yerleştirin. Ufuk ile güneşin alt kısmı arasına kaç parmağınızın sığabileceğini ölçmeniz gerekiyor. Dört parmak bir saate eşittir ve her parmak 15 dakikayı temsil eder. Bir elden daha fazla yer varsa, diğer elinizi ilk elinizin üzerine hizalayın ve buna göre sayın. Bu sayede gün batımına kaç saat kaldığını kolayca bulacaksınız.
Kaynaklar ve ileri okumalar:
- A Handy Guide to Measuring the Sky; Bağlantı: A Handy Guide to Measuring the Sky/
- Sky measurements: Degrees, arcminutes and arcseconds. Yayınlanma tarihi: 17 Temmuz 2023. Kaynak site: Bağlantı: Sky measurements: Degrees, arcminutes and arcseconds
- How to Measure Remaining Daylight With Your Hand. Yayınlanma tarihi: 11 Ekim 2018. Kaynak site: TreeHugger. Bağlantı: How to Measure Remaining Daylight With Your Hand
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










