Genelde bunaldığımızda bir de denize erişme şansımız var ise boş bir biçimde denizi seyretmeye hepimiz eğilimliyizdir. Gözlerimizi ileriye doğru dikeriz. Sonrasında da genellikle deniz ile gökyüzünün birleştiği ufuk çizgisi civarına odaklanırız. Peki ama adına ufuk veya ufuk çizgisi dediğimiz bu çizgi acaba ne kadar uzaklıktadır?

Bu sorunun cevabını bulmadan öncelikle bir kere daha hatırlatalım. Ufuk çizgisi dediğimiz yani dünya yüzeyinin ve gökyüzünün birleşmiş gibi göründüğü çizgi gerçekte olmayan bir şeydir. Gökyüzü ve deniz elbette hiçbir yerde birleşmezler. Suyun yüzeyi her ne kadar düz gibi gözükse de kavislidir ve Dünya’nın eğriliğini takip eder.
Yine de ufuk çizgisinin ne kadar uzakta olduğunu hesaplayabiliriz. Ancak cevap kişiden kişiye, daha doğrusu kişinin bulunduğu konumdan konuma değişir. Yani tek bir tanım ve tek bir rakam yoktur. Çünkü ufuk çizgisinin göründüğü yer hava koşullarından kaynaklı atmosferik kırılma nedeniyle günden güne değişmektedir. Ayrıca, gözlemcinin gözleri deniz seviyesinden ne kadar yüksekse, ufuk çizgisi gözlemciden o kadar uzaktadır.

Ufuk Çizgisi Uzaklığını Nasıl Hesaplayabiliriz?
Gözlerimiz yerden yaklaşık 30 cm yukarıdayken Dünya’nın eğriliğine takılmadan görebileceğimiz maksimum mesafe 1,5 km’dir. Ayağa kalkıp gözlerimiz yerden yaklaşık 1,7 metre yüksekte olursa ufkun uzunluğu 5 km’ye çıkar. Ne denli yüksekteyseniz ufuk çizgisi o denli uzun olur
Hesaplama kolaylığı için, Dünya’nın mükemmel bir şekilde küre olduğunu varsayalım. Şekilde, “R” Dünyanın yarıçapını, “h” bireyin yüksekliğini ve kırmızı çizgi ise hayali ufuk çizgisi ile aradaki mesafeyi temsil etmektedir. Bu mesafeyi hesaplamak için, gözlerinizin düz zeminden yüksekliğini ölçmeniz gerekir.
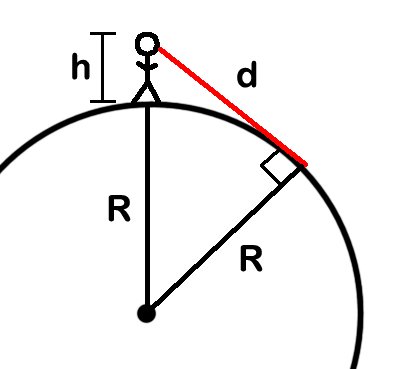
Yani h dediğimiz kişinin yüksekliği değil gözlerinin zemine olan uzaklığı kadardır. Bu değerin 1.5 metre çıktığını varsayalım. Gezegenin küresel olduğunu varsaydığımız için, dünyamızın 6378137 metre olan yarıçapını da biliyoruz. Şimdi yapmanız gereken tek şey yakinen tanıdığımız Pisagor teoremini kullanmak olacak.
Bildiğinizi düşünüyoruz ancak matematiği yeni başlayanlar için anımsatalım. Görsele göre Pisagor teoremini kullanırsak R2+d2=(R+h)2 olur. Biraz önceki değerleri de bu denklemde yerlerine yerleştirip gerekli hesaplamaları yaparsanız göz yüksekliği 1,5 metre olan bir kişi için ufuk çizgisinin yaklaşık 4,4 kilometre uzakta olduğunu bulabilirsiniz.
Ancak, bu mesafenin çok da fazla olmadığını düşünüp yine de gidip orada böyle bir çizginin olup olmadığını görmek için boşuna deneye kalkışmayın. Çünkü siz ufka doğru yaklaştıkça mesafe sürekli olarak değişecektir. Belki de bu bize bazı şeyleri ne kadar elde etmek istersek isteyelim bunun bazen mümkün olamayacağını hatırlatmanın bir yoludur!

İnsan Gözü Ne Kadar Uzaklığı Görebilir?
Az önce yaptığımız hesaplamada dünyamızın şeklinden dolayı bazı sınırlandırmalar vardı. Ancak dünyamız küresel değil de bazılarının iddia ettiği gibi düz olsaydı o zaman işler değişirdi. Aslında, bu şartlar altında bir dağın tepesinde durup gezegenimizi inceliyor olsaydınız, yüzlerce kilometre uzaktaki parlak ışıkları bile algılayabilirdiniz. Hatta karanlık bir gecede, 48 km uzakta yanan bir mumun titreyen alevini bile görebilirdiniz.
İnsan gözünün ne kadar uzağı görebileceği, uzaktaki bir nesnenin kaç tane ışık parçacığı veya foton yaydığına bağlıdır. Çıplak gözle görülebilen en uzak nesne ise, Dünya’dan yaklaşık 2,6 milyon ışık yılı uzaklıkta bulunan Andromeda galaksisidir.
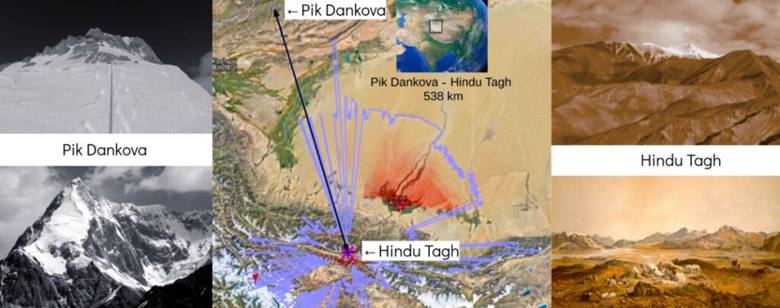
Bilgisayar modelleri Dünya’da görülebilen en uzak mesafenin Kırgızistan’daki Dankova Dağı ile Çin’deki Hindu Tagh Dağı arasındaki 538 kilometre olduğunu gösteriyor.

Kimse henüz bu iki nokta arasını fotoğraflayarak bu görüş hattını doğrulamadı. Yine de 2016’da Marc Bret adlı bir fotoğrafçı İspanya Pireneleri’ndeki Pic de Finestrelles’ten 443 kilometre uzaklıktaki Fransa Alpleri’ndeki Pic Gaspard’ı filme alarak kaydedilen en uzak görüş mesafesine imza atmıştır.
Yazının sonunda ayrıca göz atmanızı öneririz. Tarih Değiştirme Çizgisi Nedir? İki Yer Arası 3,8 Km Ama Zaman Farkı Nasıl 21 Saat Olur?
Kaynaklar ve İleri Okumalar:
- When I stand at the water’s edge and look out over the ocean, how far away is the horizon? Yayınlanma tarihi: 15 Mart 2023. Kaynak site: How stuff works. Bağlantı: ; When I stand at the water’s edge and look out over the ocean, how far away is the horizon/
- How far can the human eye see?; yayınlanma tarihi: 7 Mayıs 2012 Kaynak site: Live Science..; Bağlantı: How far can the human eye se/
- What are the limits of human vision? yayınlanma tarihi: 27 Temmuz 2015; Kaynak site: BBC. Bağlantı: What are the limits of human vision?
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel