Matematik öyle bir şey ki, onu görmediğimiz ya da kullanmadığımız bir alan var mı bilemiyorum. Başta fizik olmak üzere biyolojide hatta sosyal bilimlerde bile matematik karşımıza çıkıyor. Bir de matematik deyince aklımıza gelen ikinci bir bilim daha var: Bilgisayar bilimi. Peki sizce bilgisayar bilimiyle matematiğin arasında ne gibi bir ilişki vardır?

Aslında matematiksel mantık ve bilgisayar programlamaları, birbirlerine çok benzer hatta neredeyse aynı şeylerdir. Öyle ki bu durumu açıklayan görüşün bir ismi bile var: Curry-Howard yazışması. Curry-Howard yazışması (Curry-Howard correspondence), Maxwell’in elektrik ile manyetizmanın aynı fenomenin farklı yönleri olduğunu fark edip elektromanyetizmayı ortaya atmasına benzer bir şey yapar. Birbirinden ayrı olduğunu sandığımız bilgisayar bilimi ve matematiksel mantığı birbirine bağlar.
Basitçe ifade etmek gerekirse Curry-Howard yazışması (bazı kaynaklarda Curry-Howard izomorfizmi olarak da geçer), bilgisayar biliminden iki kavram olan tipler (types) ve programların sırasıyla matematiksel mantıktan kavramlar olan önermelere ve ispatlara eşdeğer olduğunu söyler. Yani program yazmak öylece kodlama yapmak demek değildir. Aynı zamanda bir teoremi kanıtlama eylemi demektir. Ve bu da programların doğruluğu hakkında matematiksel akıl yürütmeler yapabilmemizi sağlar.
Peki Curry-Howard Yazışması Nasıl Ortaya Çıktı?
Curry-Howard yazışması, onu bağımsız olarak keşfeden iki matematikçiden ismini alır. 1934’te matematikçi ve mantıkçı Haskell Curry, matematikteki fonksiyonlar ile mantıktaki iki önerme arasındaki “eğer-öyleyse” biçimini alan çıkarım ilişkisi arasında bir benzerlik fark etti.
Curry’nin gözleminden esinlenen matematiksel mantıkçı William Alvin Howard ise, 1969’da hesaplama ve mantık arasında çok daha derin bir bağ keşfetti. Ve bu keşfiyle de bir bilgisayar programını çalıştırmanın mantıksal bir ispatı basitleştirmeye çok benzediğini gösterdi. Peki bu ne demek?
Bir bilgisayar programı çalıştığında her bir satırı tek bir çıktı verecek şekilde değerlendirilir. Benzer bir şekilde, ispatta da bir sonuca varana kadar karmaşık ifadeleri basitleştiririz. Yani hem ispatta hem de bilgisayar programlarında birçok ara ifadeden türemiş ancak daha öz olan bir ifadeye ulaşmaya çalışırız.
Her ne kadar yukarıda Curry-Howard yazışmasının genel anlamını aktarmış olsak da bu tanım onu anlamak için yeterli değildir. Bu yüzden bilgisayar bilimcilerin tip teorisi (type theory) adını verdiği bir fenomeni anlamamız gerekiyor.
Tip Teorisi Nedir?
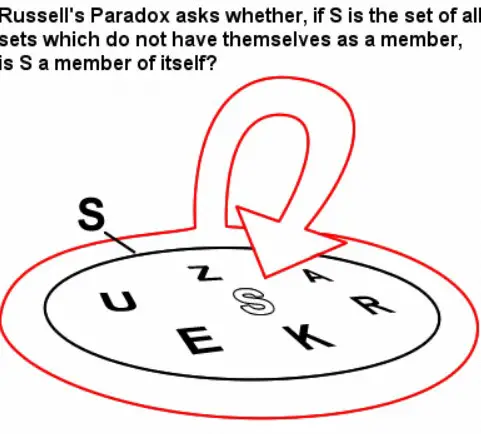
Bu teori, sezgisel küme teorisine ve biçimsel mantığa dayanan bir paradokstan kaçınmak için ortaya atılmıştır. Ve bu paradoks da Bertrand Russell’ın meşhur berber paradoksudur. Paradoksa göre bir köyde kendisini tıraş edemeyen erkekler ve kendisini tıraş edemeyen erkekleri tıraş eden bir berber yaşamaktadır. Sorumuzsa şu: Bu berber kendini tıraş eder mi etmez mi?

Eğer evet cevabını veriyorsanız bu, berberin kendisini tıraş etmemesi anlamına gelir. Çünkü berber sadece kendisini tıraş edemeyen erkekleri tıraş etmektedir. Cevabını hayırsa o zaman da berber kendisini tıraş etmelidir. Çünkü berberimiz kendisini tıraş edemeyen erkekleri tıraş etmektedir. Kısacası bir çelişki söz konusudur. Russell paradoksu olarak da bilinen bu paradoks, Bertrand Russell’ın Gottlob Frege’nin Aritmetiğin Temelleri kitabında fark ettiği bir durumdur.
Frege’nin kitabında kümeler, kendisini de içerebilen tüm olası kümeler kullanılarak tanımlanabiliyordu. Russell da bu durumun bir çelişki yarattığını fark etti. Bunu çözmek için de 1902 ve 1908 yılları arasında çeşitli tip teorileri önerdi. Buna göre belirli bir tipteki varlıklar, yalnızca o tipin alt tipleri tarafından oluşturulur. Bu sayede de bir varlığın kendisi kullanılarak tanımlanması engellenmiş olur.
İşte Curry ve Howard da tiplerin temelde mantıksal önermelerle eşdeğer olduğunu gösterdi. Bir fonksiyon, belli bir tipten bir nesne olan bir fonksiyonu tanımlayabildiğinde aslında karşılık gelen önermenin de doğru olduğunu göstermiş oluyordu.
Yani A tipi bir girdi alan ve bunu A->B olarak gösterip B tipi çıktı veren fonksiyonlar bir çıkarıma karşılık gelmelidir. Mesela bu örnek için çıkarımımız “A ise B” şeklindedir. Ya da daha açık bir örnek olması bakımından “Yağmur yağıyorsa yerler ıslaktır.” önermesini ele alalım. Tip teorisinde bu önerme “Yağmur yağıyor -> Yerler ıslaktır” şeklindedir.
Curry-Howard Yazışması Neden Önemli?
Matematik ispatlarıyla bilgisayar programları arasındaki bu bağlantı başta soyut geliyor. Fakat değil. Çünkü bu yazışma, sadece matematik ve bilgisayar bilimcilerinin çalışmaları hakkındaki düşünüş biçimlerini değiştirmekle kalmadı. Yanı sıra her iki alanda da çeşitli pratik uygulamaların önünü açtı.
Örneğin bilgisayar bilimlerinde için yazılım doğrulaması için teorik bir temel sağlar. Programcılar, istenen davranışları mantıksal önermeler açısından çevreleyerek bir programın istendiği gibi davrandığını matematiksel olarak kanıtlayabilirler. Ayrıca Curry-Howard yazışması, daha güçlü işlevsel programlama dilleri tasarlamak için de güçlü bir teorik temel sağlar.
Curry-Howard yazışması matematik içinse etkileşimli teorem kanıtlayıcıları olarak adlandırdığımız ispat asistanlarının ortaya çıkmasını sağlamıştır. Bunlar Lean ve Coq gibi ispat oluşturulmasına yardımcı olan yazılım araçlarıdır. Örneğin Coq’da ispatın her adımı aslında esasen bir programdır. Ve ispatın geçerliliğini de tip algoritmaları kontrol eder. Bu da matematiğin informal dilinin bilgisayarlar tarafında kontrol edilmesini sağlar.
Kaynaklar ve İleri Okumalar
- The Deep Link Equating Math Proofs and Computer Programs ; Yayınlanma tarihi: 11 Kasım 2023. Kaynak site: Quanta Magazine. Bağlantı: The Deep Link Equating Math Proofs and Computer Programs | Quanta Magazine ;
- Curry–Howard correspondence ; Bağlantı: Curry–Howard correspondence – Wikipedia
Matematiksel










