20. yüzyılın en etkili matematikçilerinden, mantıkçılarından ve filozoflarından biri olan Bertrand Russell, modern dönemin en ünlü ve en etkili mantık paradokslarından biriyle anılmaktadır. Eski paradokslar—örneğin Zeno’nun paradoksları—genellikle mantık ve akıl yürütmenin doğasını sorgularken, Russell Paradoksu, küme kavramına odaklanmıştır.

Russell Paradoksu Nedir?
Russell Paradoksu, naif küme teorisi (naive set theory) ile ilgilidir. Burada “naif” kelimesi, küçümseyici bir anlam taşımaz. Sadece formel mantık aksiyomları üzerine inşa edilmemiş, sezgisel olarak tanımlanmış küme teorilerini ifade eder. Bu küme teorisi, matematikçiler tarafından 19. yüzyılın sonunda geliştirilen orijinal küme teorisidir.
Matematiksel mantık, argümanları ve akıl yürütmeleri incelemek için yapay olarak oluşturulan biçimsel diller kullanır. Buna karşın naif küme teorileri, doğal dillerde bulunan sezgisel tanımlarla başlar ve bu dillerin içsel çelişkileriyle mücadele eder.
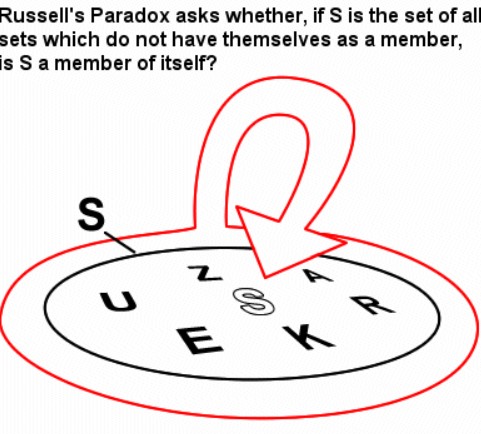
Paradoksun temel noktası, hem kendisinin elemanı olan hem de kendisinin elemanı olmayan kümelerle ilgilidir. Kısaca, bazı kümelerin kendi kendilerinin elemanı olup olmadığını sorgular ve bu durumun bir çelişkiye yol açtığını gösterir.
Matematikçilerin ve mantıkçıların kullandıkları terimlerle paradoksu size açıklamamız yazının anlaşılmasını zorlaştıracaktır. Bu nedenle Russell Paradoksu denildiği zaman akla gelen ilk örnek ile konuyu aktarmaya çalışalım.
Bu bağlamda Berber Paradoksu iyi bir başlangıç noktasıdır. Bir köyde berber, kendini tıraş etmeyen tüm erkekleri tıraş etmektedir ve yalnızca kendini tıraş etmeyenleri tıraş etmelidir. Berber kendini tıraş eder mi?

- Eğer berber kendini tıraş etmiyorsa, o halde tıraş edilmeyen erkekler grubuna girer ve onu tıraş etmesi gerekir. Ancak berber, kendini tıraş etmeyenleri tıraş ettiği için bu durumda kendisini tıraş etmek zorunda kalır.
- Eğer berber kendini tıraş ederse, o halde kendini tıraş eden biri olur. Kural gereği berberin onu tıraş etmemesi gerekir. Ancak berberin işi, kendini tıraş etmeyenleri tıraş etmek olduğundan bu durumda da kendini tıraş etmemesi gerekir.
Bu döngü, mantıksal bir çelişki doğurur. Berber hem kendini tıraş etmeli hem de etmemelidir, bu ise imkânsızdır. Benzer şekilde, Russell Paradoksu da küme teorisinde benzer bir çelişkinin ortaya çıktığını gösterir.
Russell’ın Paradoksuna, Gottlob Frege’nin Katkısı Nedir?

Bertrand Russell, Russell Paradoksu’nu, Alman matematikçi, mantıkçı ve filozof Gottlob Frege’nin kümeler hakkındaki görüşlerine karşı bir eleştiri olarak ortaya koydu. Frege’nin temel amacı, matematiğin tamamının mantığa indirgenebileceğini göstermekti. Ancak Russell, onun küme teorisinde ciddi bir çelişki olduğunu fark etti.
Frege’ye göre her özellik, kendisine sahip olan nesnelerin oluşturduğu bir kümeye karşılık gelir. Örneğin, “Kırmızı olmak” özelliği, evrendeki tüm kırmızı nesneleri içeren bir küme oluşturur. Yani, herhangi bir özellik tanımlandığında, bu özelliğe sahip olan tüm nesneleri içeren bir küme otomatik olarak var olmalıdır.
Ancak Russell, bu görüşe meydan okudu. “Kendinin elemanı olmayan tüm kümelerin kümesi” tanımlandığında büyük bir çelişki ortaya çıktı.
- Bu küme kendinin elemanı mı?
- Eğer kendinin elemanıysa, tanıma göre olmamalıdır.
- Eğer kendinin elemanı değilse, tanıma göre olmalıdır.
Bu durum, mantıksal bir çelişkiye yol açtı ve Frege’nin matematik sisteminin eksikliğini gösterdi. Frege, Russell’ın eleştirisini “Aritmetiğin Temel Yasaları” (Grundgesetze der Arithmetik) adlı kitabının ikinci baskısını yayınlamadan hemen önce aldı. Paradoksun ortaya koyduğu problemi hemen kabul etti. Sonrasındae kitabına bir ek yazarak sorunun çözülmesi gerektiğini belirtti.

Russel Paradoksu ile Küme Kavramına Yeni Bir Bakış Açısı Kazandırdı
Russell Paradoksuna yönelik çeşitli çözümler önerilmiştir. Bunlardan en doğal olanlarından biri, Bertrand Russell’ın kendisi tarafından geliştirilmiştir. A.N. Whitehead ile birlikte geliştirdiği bu çözüm, paradoksu önlemek için tüm ifadeleri belirli bir hiyerarşi içinde düzenlemeyi amaçlamaktadır. Böylece, bir nesnenin tanımı, onu içeren koleksiyonun tamamına bağlı olamaz.
Russell’ın sunduğu bu hiyerarşik çözüm, küme teorisinin temel prensiplerini daha sağlam bir zemine oturtmayı hedeflemiştir ve modern mantık çalışmalarına önemli bir katkı sağlamıştır. Ancak bu, tek geçerli çözüm değildir. David Hilbert, bu soruna “formalist” bir yaklaşım getirerek yalnızca sonlu ve iyi tanımlanmış nesnelerin kullanılmasını savunmuştur. Formalizme göre, matematik tamamen semboller ve belirli kurallar çerçevesinde işleyen bir sistemdir. Çelişkili veya belirsiz kümeler, bu sistemin dışında bırakılmalıdır.
Diğer bir alternatif yaklaşım, Luitzen Brouwer tarafından geliştirilen “sezgicilik” (intuitionism) görüşüdür. Sezgiciliğe göre, bir matematiksel nesnenin var olduğunu iddia etmek için, onun nasıl inşa edileceğini açıkça gösterebilmek gerekir. Başka bir deyişle, sadece var olduğu söylenen, ancak somut bir şekilde oluşturulamayan nesneler matematikte kabul edilemez.
Bu üç farklı yaklaşım matematiksel tutarlılığı sağlamak amacıyla geliştirilmiştir. Bunun yerine, günümüzde en yaygın kullanılan aksiyomatik küme teorisi, tipler teorisinden kaçınan ve yalnızca belirli aksiyomlarla tanımlanabilen kümelerden oluşan bir evren oluşturan Zermelo-Fraenkel küme teorisi (ZF) olmuştur.
Bu teori, küme kavramını mantıksal olarak daha sağlam bir temele oturtmayı amaçlar. Russell Paradoksu gibi çelişkileri önlemek için, her kümenin ancak belirli aksiyomlar çerçevesinde tanımlanabileceği kabul edilir. Böylece, kendini içermeyen kümelerin kümesi gibi problemli ifadeler ortadan kaldırılır.
ZF küme teorisi, matematiksel yapıların büyük bir kısmını tanımlamak için yeterince güçlüdür ve modern matematikte kullanılan standart küme teorisi hâline gelmiştir. Daha sonra bu teoriye Seçim Aksiyomu (Axiom of Choice) eklenerek ZFC küme teorisi oluşturulmuş ve bu sistem, günümüzde matematikçilerin büyük çoğunluğu tarafından benimsenmiştir.
Sonuç olarak
Russell Paradoksu, mantık, matematik ve felsefede büyük bir kriz yaratmıştır. Hiyerarşik sistemler, formel matematik ve sezgicilik gibi yaklaşımlar, bu paradoksun getirdiği çelişkileri gidermek için geliştirilmiş olsa da, her biri kendi içinde avantajlar ve zorluklar barındırır.
Bu paradoksun keşfi, küme teorisinin ve mantığın temel prensiplerini yeniden değerlendirmeye yol açmış, matematiğin daha sağlam temeller üzerine inşa edilmesini sağlamıştır.
Kaynaklar ve ileri okumalar:
- Russell’s Paradox: Here’s Why Math Can’t Have A Set Of Everything. Yayınlanma tarihi: 25 Kasım 2023. Kaynak site: Business Insider. Bağlantı: Russell’s Paradox: Here’s Why Math Can’t Have A Set Of Everything/
- Dunne, Luke. “Bertrand Russell’s Paradox Explained” TheCollector.com, December 22, 2022, https://www.thecollector.com/bertrand-russell-paradox-explained/.
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





