Çeşitli mekanik problemlerin tartışıldığı, “Mechanica” (Yunanca: Μηχανικά) isimli kitap otuz beş soruyu kapsayan bir derlemedir. Bu kitabın, Platon’un öğrencisi ve Büyük İskender’in öğretmeni olan Aristoteles (MÖ 384–322) tarafından yazıldığı kesin olmasa da, kitabın içerdiği problemler, genellikle onun adı ile anılır. Bu durum çember ya da tekerlek paradoksu için de geçerlidir.

Kitabın 15. Probleminde yazar, kıyıda bulunan çakıl taşlarının şeklinin aşınmaları ile ilişkisini tartışmaktadır. Bu olgunun altında yatan neden ise 24. problemde açıklanmıştır ve Aristoteles’in Çember Paradoksu olarak bilinir.
Temelde tüm çemberlerin aynı çevreye sahip olması gerektiğini gösteren bu paradoks bize önemli bir matematiksel argüman vermektedir. Bu argümanı yeniden yapılandırmak, matematikçileri çok uzun bir süre rahatsız eden garip bir gerçek sayı özelliğini ortaya çıkarmıştır.

Çember Paradoksu Nedir?
Bu paradoksu incelememiz için önce büyük çember, sonra o büyük çemberin içine bir de küçük çember çizmemiz gerekecektir. Paradoks şu biçimdedir. Şekilde soldaki büyük tekerleğin yere değdiği noktadan sağa doğru tam tur yuvarlandığını varsayıyoruz. Sonucunda tekerlek, çevresine eşit bir mesafede hareket edecek ve büyük tekerleğin alt kısmı, aşağıda gösterilen kesikli çizgi parçası AB’yi izleyecektir.

Ancak içteki küçük tekerleğin çevresinin büyük tekerleğin çevresinden daha az olduğunu biliyoruz. Ancak aldıkları yola dikkat ederseniz, A′B′ uzunluğu ile AB uzunluğu birbirine eşittir. Bu durumda küçük çemberin çevresiyle büyük çemberin çevresi birbirine eşit olmalıdır.
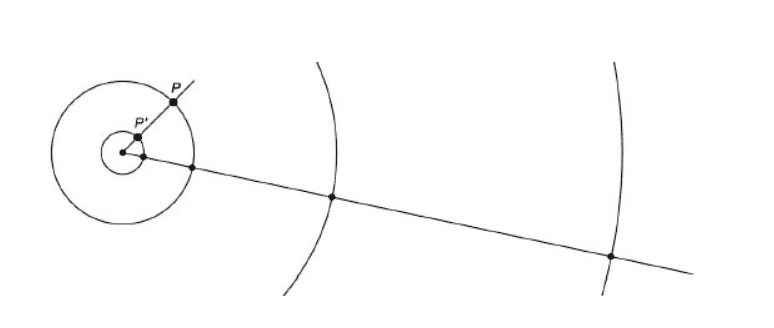
Sonucun hatalı olduğunu bilsek bile, bunu destekleyen ilginç bir matematiksel argüman bile elde ederiz. Büyük daire üzerindeki noktalar ile daha küçük daire üzerindeki noktalar arasında bire bir eşleme yapalım. Çemberlerin merkezinden çıkan herhangi bir ışın ikisini de kesecek ve böylece iki çember üzerindeki noktalar arasında açık bir ilişki (bire bir) kuracaktır.
Herhangi bir çemberin çevresi etrafında kaymadan bir tam tur döndüğünde kat edebileceği mesafenin, çemberin çevre uzunluğuna eşit olduğunu biliyoruz. Örneğin r birim yarıçaplı bir tekerleğin, çevresi etrafında kaymadan bir tam tur döndüğünde alabileceği mesafe 2πr’dir. Peki iki tekerleğin kat ettiği mesafeler nasıl aynı oluyor?
Çember Paradoksunun Çözümlemesi
Aslında internette yapacağını kısa bir araştırmada bu sorunun farklı cevapları olduğunu göreceksiniz. Bu paradoksun ilginç yanı hem matematiksel hem de fiziksel bir açıklamasının olmasıdır. Bu cevaplardan en basit olanının açıklaması aşağıdaki gibidir.

Fiziksel açıklaması aslında akla ilk gelen açıklamadır. Sonucunda bu yol üzerinde her iki tekerleğin aynı anda hareket etmesi imkansızdır. Hata, her iki çemberin de aynı mesafeyi yuvarlayacağı varsayımında yatmaktadır. Oysa ki büyük tekerlek A noktasından B noktasına düzgün bir şekilde yuvarlanırken, küçük tekerlek için aynı şey geçerli olmaz. Her iki tekerleğin de kaymadan hareket etmesi fiziksel olarak imkansızdır.
Ancak sorunu matematiksel olarak ele alırsak daha incelikli bir cevaba ulaşırız. Aslında bu paradoks ile ilgilenen pek çok matematikçi olmuştu ve bu kişilerden birisi de Galileo idi. Kendisi probleme eşmerkezli düzgün çokgenlerin hareketinin bir analizini geliştirerek (altıgenlerle başlıyor) yaklaştı.
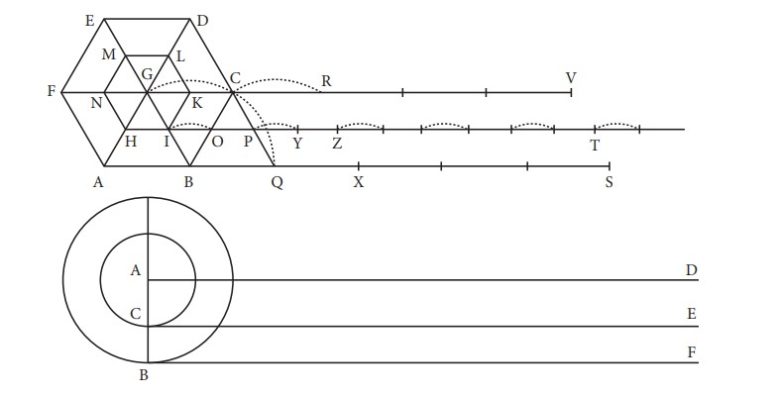
Örneğin altıgen şeklindeki tekerlekler bir tam tur döndürüldüğünde, ilk ve son konumda tekerleklerin merkezleri arasındaki mesafe birbirine eşit olur. Fakat büyük tekerlek tüm yolu tamamlarken, küçük tekerlek yolun bazı bölümlerini atlayarak yol alır. Ancak tekerleğin kenar sayısını arttırdığımız zaman bu atlanan bölümler kısalır.
Bunun neticesinde Galileo, çok sayıda kenara sahip düzgün bir çokgenin sezgisel olarak çembere benzediğini ve bu tekerlekler döndüğünde küçük tekerleğin yolu yine atlayarak tamamlayacağını düşündü. Kendisinin pek çok düşüncesi doğru olsa da bulduğu cevap hatalı olacaktı.
Sonuç olarak
Çember paradoksunu matematiksel olarak ele alırsak da sorun AB ve CD doğruları gibi birebir eşleşen herhangi iki doğrunun aynı uzunluğa sahip olduğu yanılgısını ortaya çıkar. İki doğrunun tüm noktaları arasındaki bire bir eşleşme, doğruların aynı uzunluğa sahip olduğu anlamına gelmez. Örneğin aşağıdaki koyu renkli iki doğru parçasının uzunlukları birbirine eşit değildir. Amca yine de noktalar arasında birebir bir eşleşme vardır.
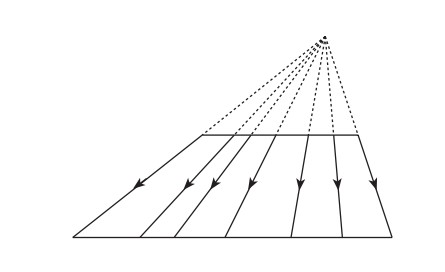
Herhangi iki eğri üzerindeki noktaların bire bir eşleşmesinin eğrilerin aynı uzunlukta olmasını gerektirmediğini kanıtlayarak, Aristo’nun çember paradoksunu çözen ilk kişi ise Alman matematikçi George Cantor’dur. Paradoksun çözüm anahtarı ise süreklilik ve sonsuz kümeler kavramlarıdır.
Kaynaklar ve ileri okumalar için:
- Gal, Ofer & Chen-Morris, Raz. (2012). Nature’s drawing: Problems and resolutions in the mathematization of motion. Synthese. 185. 10.1007/s11229-011-9978-5.
- Lopes, Renato & Ferigolo, Jorge. (2024). Taphonomic significance of Aristotle’s ‘Wheel Paradox. An example with the cerithid gastropod Cerithium atratum (Born, 1778) from Conceição Lagoon. Santa Catarina State, Southern Brazil. Revista Brasileira de Paleontologia. 26. 272-287. 10.4072/rbp.2023.4.03.
- Satisfying explanation of Aristotle’s Wheel Paradox.; https://math.stackexchange.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel