Gündelik hayattaki hemen hemen her şeye uygulanan, ancak bilim dünyasının dışında fazla da bilinmeyen bir fikir söyle derseniz vereceğimiz cevap muhtemelen Fourier dönüşümü olacaktır.
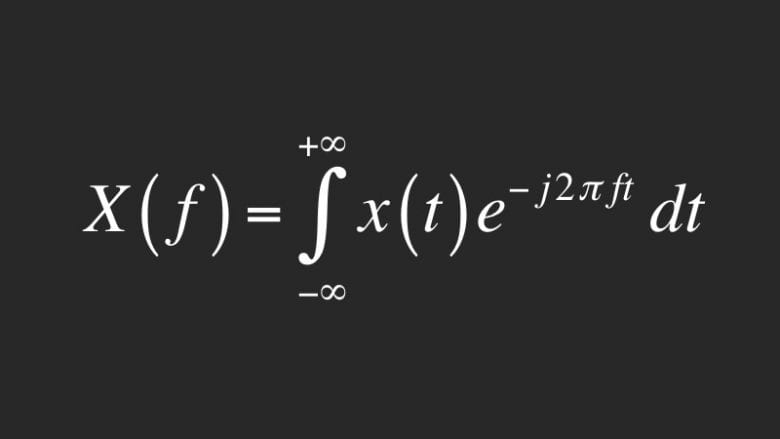
Fransız matematikçi ve fizikçi Jean Baptiste Joseph Fourier tarihteki bazı bilimciler kadar meşhur değildir. Ama çalışmaları fotoğraftan deprem analizine kadar çeşitli alanlarda uygulanma olanağı bulmuştur. Bilgisayarınıza bir şarkı indirdiğinizde veya MP3 çalarınızda bir dijital müzik dosyası çaldığınızda Fourier dönüşümü formülünü kullanırsınız. İnternette gördüğünüz fotoğrafları JPG formatına dönüştüren, hatta ses geçirmez kulaklıklarınızın çalışmasını sağlayan da bu denklemdir.
Bu denklem temelde Joseph Fourier’in 1822’de yazdığı Isının Analitik Teorisi isimli kitabında yer alır. Aslında kendisi ısının malzemeler içinde ve etrafında nasıl aktığıyla ilgilenmekteydi. Bu olguyu çalışırken, aklına karmaşık yollarla değişen nicelikleri, dalgalardan oluşan çok basit bileşenlere ayırma fikri geldi.

O zamanlar önemli bir buluş yaptığının farkında değildi. Ancak onun bulguları ilerleyen süreçte bilim insanlarının dalgalardan oluşan hemen her şeyde ( ses, ısı, ışık, hisse senedi fiyatları) karmaşık bir süreci basitleştirmek için bu denklemi kullanmasına neden oldu. Gelin nasıl çalıştığına bir bakalım…
Fourier Dönüşümü Nedir?
Fourier Dönüşümü ismi size ilk etapta tuhaf gelecektir. Ancak aslında yaptığı şey oldukça basittir. Zor görünmesinin nedeni de aslında formülde karşımıza çıkan ifadelerdir. Elinizde bir kağıt banknot varsa ve minibüse bindiğiniz zaman şoförün bu paraya itiraz edeceğini bilirsiniz. Bu nedenle de paranızı bir yerlerde bozdurmak zorunda kalırsınız. Bir kağıt para karşılığında bir sürü bozuk para elde edersiniz. Harcamanızı yaptıktan sonra da bozuk paralarınızı bir yerlerde yeniden bütünlersiniz.
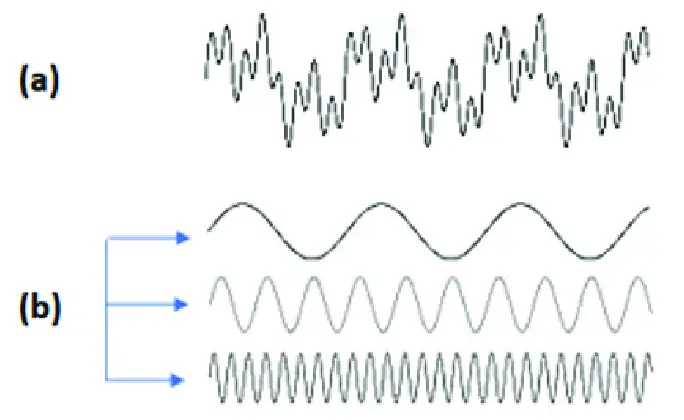
İşte Fourier Dönüşümü de tam olarak aslında bu işi yapar. Ancak paralar ile değil bu sefer dalgalar ile uğraşır. Karmaşık dalgaları alır ve basit sinüs dalgalara ayırır. Daha sonrasında da basit dalgaları tek bir karmaşık dalga olacak biçimde birleştirir.
Diğer bir deyişle, Fourier’in çalışmasının gösterdiği şey, karmaşık dalgaların, farklı frekans ve genliklerdeki bir dizi sinüs dalgasının birbirine eklenmesi ile ortaya çıktığıdır. Bu yöntemlerini kristalografi, optik, sinyal işleme ve jeofizik gibi alanlarda son derece değerli hale getirir. ( Daha fazlası için göz atmak isterseniz: Fourier Serisi: Basit Bir Buluş Birçok Sırrın Kilidini Nasıl Açtı??
Fourier Dönüşümü Ne İşe Yarar?
Ses mühendisleri bir ses kaydını MP3 dosyasına dönüştürmek istediklerinde, ses dalgasının ayrı ayrı frekanslarını ortaya çıkarmak ve her an genliklerini not etmek için Fourier dönüşümünü kullanırlar.
Ses, basit sinüs eğrilerine dönüştürülebilirse bunun tersi de geçerli olmalıdır. Yani gerektiği zamanlarda, sinüs dalgaları herhangi bir sesi yeniden oluşturmak veya sentezlemek için bir araya eklenebilecektir. Modern elektronik müzik sentezleyicilerinin ilkesi budur.
Ayrıca Fourier dönüşümü dosyaları sıkıştırmak istediğimizde de bize destek olur. Aslında veri sıkıştırma sürecine cebir, istatistik, çizge teorisi, Fourier analizi ve fraktallar dahil olmak üzere bir dizi matematiksel konu katkıda bulunmaktadır. Bu yöntem aynı zamanda bir kaydı temizlemek istediğinizde de yararlıdır. Arka planda rahatsız edici bir ses varsa, Fourier dönüşümü ile sesi bileşenlerine ayırıp o sesi ortadan kaldırmanız mümkün olur.

Ses Harici Alanlarda Fourier Dönüşümü
Fourier dönüşümleri, seslerin dışında görüntülerin analizi ve manipülasyonu için inanılmaz derecede faydalı araçlardır. Özellikle görüntüler için, görüntü sıkıştırmanın (JPEG formatı gibi), görüntüleri filtrelemenin ve bulanıklığı azaltmanın arkasındaki matematiksel makine gibidirler.
Bir görseli JPG olarak kaydettiğinizde, tüm görüntü daha küçük parçalara bölünür. Sonrasında bloğun 2 boyutlu Fourier dönüşümü alınır. Bu, görüntünün bu küçük parçası üzerinde renk ve parlaklığın nasıl değiştiğine dair uzamsal frekansların bir tanımını sağlar. Bu esnada görsele keskinlik ve netlik veren bazı yüksek frekanslı parçaları atar. Bu fazlalık frekanslardan kurtulmak görselin kalitesini bozmaz.
Kimyacılar, Fourier dönüşümlü kızılötesi spektroskopisi gibi yöntemler kullanarak bilinmeyen maddeleri analiz etmek için trigonometriye güvenirler. Fourier spektroskopunun öncüsü 1880’de icat edilmiş olmasına rağmen, gerçek hayattaki Fourier dönüşümü hesaplamaları o kadar zaman alıcıdır ki, 1950’lerde dijital bilgisayarlar yaygınlaşana kadar Fourier dönüşüm spektroskopisinin pratik uygulamaları sınırlıydı.

Hızlı Fourier dönüşümü veya FFT olarak bilinen özellikle verimli bir hesaplama yönteminin 1956’da sonraki keşfi, Fourier dönüşüm spektroskopisinin pratik gelişimine yol açan büyük bir ilerlemeydi. Hızlı Fourier dönüşümleri o zamandan beri dijital ses işleme, dijital görüntü işleme ve sismik veri işleme için önemli bir hesaplama aracı haline geldi.
Fourier dönüşümleri, ayrıca MRI ve CAT taramaları dahil olmak üzere tıbbi görüntülemedeki bilgileri işlemek ve hatta depremlerde binaları yıkılmaya karşı korumak için de kullanılır. Bitti mi daha bitmedi.
Depremler ve Dönüşümler
Yer sarsıldığında, bir Fourier dönüşümü size hangi titreşim frekanslarının çevrelerine en fazla enerji verdiğini gösterecektir. Bir deprem esnasında, binalarda kendi doğal frekansında titreşir. Depremin neden olduğu titreşimler binanın doğal frekansıyla eşleşirse, titreşimler yükselir. Bunun sonucunda da binanın hasar görme ihtimali artar. Mimarlar ve inşaat mühendisleri, bilgisayar modellerini kullanarak yerel depremlerin Fourier dönüşümünden gelen bilgileri inceler. Daha sonra binanın frekansını, ayakta kalma olasılığı en yüksek olacak şekilde ayarlamaya çalışır.
Sonuçta bizce tüm bunlar basit bir denklem için gerçekten fazlasıyla etkileyicidir. Bu yazıda denklemin matematiksel olarak nasıl elde edildiğine değinmek istemedik. Ancak merak edenler bu yazıya göz atabilirler.
Kaynaklar ve ileri okumalar:
- Digital Music Couldn’t Exist Without the Fourier Transform; Yayınlanma tarihi: 30 Mayıs 2016; Bağlantı: Digital Music Couldn’t Exist Without the Fourier Transform/
- Fourier transforms of images; yayınlanma tarihi: 7 Nisan 2017; Bağlantı: https://plus.maths.org/
- The Fourier transform lets you have your cake and understand it. Yayınlanma tarihi: 13 Temmuz 2014; Bağlantı: https://www.theguardian.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel