Pasta kesmek ile matematiğin ne ilgisi var demeyelim. Pasta kesme problemi özünde, herkesin kendi payına düşenden memnun kalması için bir pastayı masadaki insanlar arasında paylaştırmanın en iyi yolunu bulmakla ilgilenir.

Bu kadar önemsiz bir sorunun neden yüzyıllardır matematikçileri büyülediğini merak etmiş de olabilirsiniz? Cevap, pastanın gerçekten paylaşılabilecek herhangi bir malın veya kaynağın bir metaforu veya temsili olduğu gerçeğinde yatmaktadır. Ancak aslında bakarsanız pata kesmenin matematiği gerçek bir pasta meraklısının çalışmaları ile başlamıştır.
Francis Galton (1822-1911) Kraliçe Viktoriya çağında yaşamış çok yönlü bir İngiliz bilim insanıdır. Uğraş gösterdiği alanlar arasında coğrafya, meteoroloji, psikoloji, kriminoloji, genetik bilim, öjenik ve istatistik vardır. Ancak anlaşılan kendisi pasta kesme ile de ilgilenmekteydi. 1906 yılında Nature dergisine pasta kesmenin bilimsel ilkeleri hakkında yazdığı bir mektupta mevcut pasta kesme biçiminin hatalı olduğunu dile getirmişti. Sonrasında da ilginç bir öneride bulunacaktı.

Elbette Galton bu öneriyi yaparken yemek yapmak ile ilgilenmiyordu. Sonucunda onun asıl tutkusu ölçümler üzerineydi. Londra’nın merkezinde, halktan insanların geçerken uğrayıp boylarının, kilolarının, kavrama güçlerinin, soluk alma şiddetlerinin, görüş mesafelerinin ölçülebileceği bir antropometrik kütüphane oluşturmuştu. Kütüphanede 10.000’den fazla insanın ölçümlerinin bir derlemesi vardı.
Genç bir bilim insanıyken, günlük olarak çaydanlığın sıcaklığı, kullanılan kaynar su miktarı ve çayın ne kadar lezzetli olduğuna dair veriler topladı. Amacı mükemmel lezzetli bir fincan çayın nasıl yapılacağını bulmaktı. Aslında beş çayı matematiği onun için yaşam boyu bir tutku olmayı sürdürdü. Yaşlı bir adamken de bir pastayı mümkün olabildiğince uzun süre taze tutmak amacıyla en iyi nasıl kesileceğini göstermek için Nature dergisine aşağıdaki diyagramı yolladı.
Galton’un Önerdiği Yöntem Nedir?
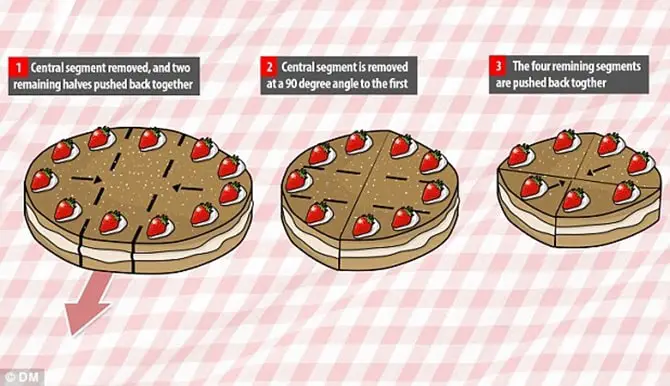
Yuvarlak bir keki bilimsel prensiplere göre kesmek adlı diyagramda Galton bir pastanın nasıl kesilmesi gerektiğini yukarıdaki gibi göstermişti. Onun ifadesine göre bu yöntem geleneksel dilimlemenin neden olduğu kekin içinin kurumasını en aza indiriyordu. İşlemin ikinci ve üçüncü aşamalarında ise kek elastik bir bantla bir arada tutuluyordu.
Bunu pratik olarak şu biçimde düşünebiliriz. Önce pastanızı çapın bir parmak sağ, bir parmak sol tarafından olmak üzere baştan başa kesin. Sonrasında ortada oluşan ince uzun dilimi çıkartıp afiyetle yiyin. Devamında da kalanı saklamak için iki yarım çemberi hafifçe ittirerek birleştirin.
Pasta tekrar kesileceği zaman bu kez daha önceki kesiğe paralel değil, bu kesikleri dik kesecek şekilde pastanıza biraz önce anlattığımız biçimde kesin. Sonrasında da yine oluşan dilimi çıkarın. Ancak bu sefer geriye kalan dört parçayı birleştirin. 3. güne gelindiğinde, kalan dilimleri bir daire olacak biçimde birleştirin ve ilk gün yaptığını kesimi tekrarlayın.
Yukarıda aktardığımız teknik iki boyutta alıştığımız pasta kesme tekniğine bir alternatif. Peki ama dört boyutlu uzayda bir pasta kesiyor olsaydık ne olurdu? Sonuçta hayal gücünün sınırı yoktur. Aslında matematikçiler yakın zamanda bu konuya da el attılar. Ancak onların da temelde ilgilendikleri şey pasta kesmek elbette değildi.
N- Boyutlu Uzay Eşit Pasta Dilimlerine Nasıl Bölünür?
Aslında bakarsanız Massachusetts Teknoloji Enstitüsü’ndeki (MIT) araştırmacıların amacı, 50 yıldan daha eski olan eşkenar çizgilerle ilgili bir geometri problemini çözmekti. Problem, n-boyutlu uzayların teorik olarak eşit pasta dilimlerine nasıl bölüneceğini araştırıyordu.

Konuyu özetle şu biçimde aktarabiliriz. Herhangi bir pastayı 6 eşit parçaya düzgün bir biçimde ayırdığımızı düşünelim. Bu durumda merkez etrafında her biri 60 derecelik 6 tane eş açı oluşacaktır. Pastamızı 8 parçaya bölersek de bu eş açılar bu sefer 45 derece olacaktır. ( Bunu anlamak için gerçekten pasta kesmenize gerek yok. Bir pergel yardımı ile bir kağıdın üzerine düzgün bir çember çizin ve onun üzerinde inceleyin. Şu an iki boyutlu bir pastaya sahipsiniz)
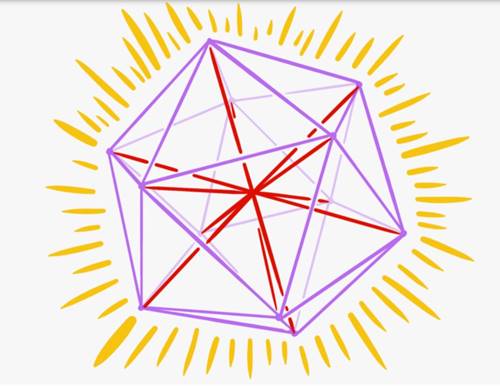
Şimdi üç boyutlu bir pastayı düşünelim. Bu pastayı 6 dilime ayırırsak bu sefer üç boyutlu uzayda eş açılı üçgenleri düşünmemiz gerekiyor. Daha yüksek boyutlar işin içine karıştığı zamanlarda da artık bu pasta hayal gücümüzün ötesine geçiyor. Bu nedenle yaklaşık 50 yıldır matematikçiler yüksek boyutlarda eş açıları belirlemenin bir yolunu bulmaya çalışıyorlardı.
Bunun için de araştırmacılar spektral çizge teorisinden yararlanmaya karar verdiler. Bu matematiksel yöntem grafikleri ve ağları anlamak için lineer cebirden faydalanır. Bir çizgenin “spektrumu”, bir grafiği matrise dönüştürerek ve özdeğerlerine bakarak elde edilir. Sonrasında da bu matrisler matematikçilerin hesaplama yapmasını kolaylaştırır.
Sonuç olarak
Kimimiz bir pastayı sadece lezzeti için severken, eğer bir matematikçiyseniz, konuya bambaşka bir bakış açısı ile bakabilirsiniz. Aslında bu yazıda ele aldığımız pasta kesmek ve matematik ile ilişkili yapılan çalışmalardan sadece bir tanesidir. Bir pastayı sınırlı sayıda adımda adil bir şekilde bölme sorunu ile ilgili de matematikçiler pek çok çalışma yapmaktadır. Pastayı pasta olarak değil de adil biçimde paylaşılması gereken arazi olarak düşünürseniz, yaptıkları çalışmanın önemini anlamanız daha kolay olacaktır.
Sonuçta bir matematikçinin nereden iham alacağı asla belli olmaz! Madem konuyu tatlı açtık, tatlı kapatalım. Bu yazımızda da kek yapmanın arka planını sizlere anlatalım. Mutfağınız Laboratuvarınız: Kek Yapmanın Ardındaki Bilime Göz Atalım
Kaynaklar ve ileri okumalar:
- Cut Your Cake And Keep It (Fresh), Too; Yayınlanma tarihi: 19 Haziran 2014. Bağlantı: Cut Your Cake And Keep It (Fresh), Too/
- How to Slice a Pie in Four Dimensions, According to Math. Yayınlanma tarihi: 16 Mayıs 2022. Kaynak site: Popular Mechanics. Bağlantı: How to Slice a Pie in Four Dimensions, According to Math/
- Mathematicians solve an old geometry problem on equiangular lines. yayınlanma tarihi: 4 Ekim 2021. Kaynak site: MIT News. Bağlantı: Mathematicians solve an old geometry problem on equiangular lines
- Jiang, Zilin & Tidor, Jonathan & Yao, Yuan & Zhang, Shengtong & Zhao, Yufei. (2019). Equiangular lines with a fixed angle.
- The Obsession of Mathematicians With How To Divide a Cake. Yyaınlanma tarihi: 9 Kasım 2023. Kaynak site: BBVA OPen Mind. Bağlantı: The Obsession of Mathematicians With How To Divide a Cake
- The Mathematics of Cake Cutting. Yayınlanma tarihi: 13 Ekim 2016. Kaynak site: Scientific Americab. Bağlantı: The Mathematics of Cake Cutting
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel