Her tür oylama sistemi sorunları ile birlikte gelir. Bu nedenle matematikçiler yüzyıllar boyunca adil bir seçim sistemi bulmak için çabalamıştır ve daha iyi veya daha adil bir sistem bulma girişimleri, ekonomist Kenneth Arrow’un “imkansızlık teoremi”ni yayınladığı 1950’ye kadar devam etmiştir.

Mükemmel bir oylama sistemi var mı? 1950’lerde ekonomist Kenneth Arrow kendine bu soruyu sordu. Arrow aksiyomatik yaklaşımı seçti. Gerçek seçim sistemlerini önermek ve analiz etmek yerine, yerine getirilmesi gereken bir dizi makul kriter ortaya koydu.
Oylama Paradoksu Diğer Adıyla Arrow İmkansızlık Teoremi Nedir?
Mevcut tüm seçmenlerin tüm olası adayların sıralamasını sağladığını ve bu bildirilen sıralamaları kullanarak toplam bir sıralama elde etmek istediğimizi varsayalım. Bu amaçla yapacağımız bir seçimin aşağıdaki kuralları karşılamasını bekleriz.

- Eğer her seçmen aday A’yı aday B’den daha çok tercih ederse, o zaman toplam sıralama A’yı B’den önce koymalıdır. Diğer bir deyişle oybirliği olmalıdır.
- Tek bir kişinin oyu diğer herkesin oyunu geçersiz kılmamalıdır. Başka bir deyişle, hiçbir seçmen tek başına diktatör gibi davranıp diğer seçmenlerin tercihlerini geçersiz kılamaz. Seçmenlerin tercihleri herhangi bir biçimde etkilenmemelidir.
- Eğer her seçmenin A ile B arasındaki tercihi aynı kalırsa, A ve B’nin toplam sıralamadaki göreli sırası da değişmemelidir.
- Oylama sistemi geçişli olmalıdır. Yani bir seçmen A’yı B’ye ve B’yi C’ye tercih ediyorsa A’yı da aynı zamanda C’ye de tercih etmelidir.
- Başka bir seçeneğin tanıtılması seçimin sonucunu etkilememelidir.

Arrow’un kanıtladığı şey, üç veya daha fazla adayın olduğu bir oylama sisteminde, bu koşulların beşinin tamamının karşılanmasının matematiksel olarak imkansız olduğuydu. Başka bir deyişle, hangi oylama sistemi seçilirse seçilsin, aksiyomlardan biri er yada geç ihlal edilecekti. Onun bu bulgusu oylama paradoksu ya da Arrow imkansızlık teoremi olarak biliniyor. İlginçtir ki, Arrow’un tanımladığı paradoks, üçten az aday olduğunda ortadan kalkar. İki aday için, çoğunluğun tercih ettiği adayı seçmek, beş koşulu da karşılar.
Arrow İmkansızlık Teoremi İçin Bir Örnek
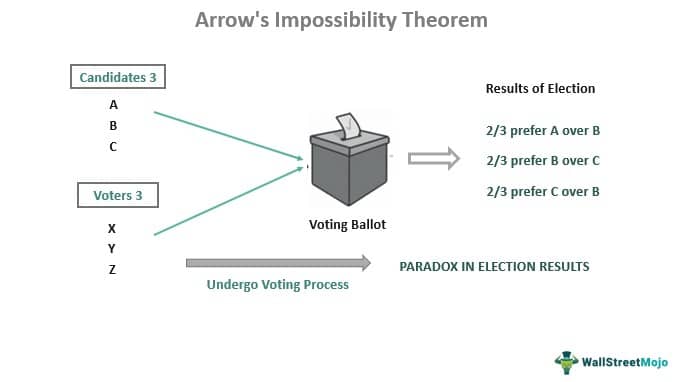
Diyelim ki üç projenin oylanması gerekiyor. Bu projeler bir kere daha A; B; ve C biçiminde olsun. Oy kullanacak 99 kişi var. Oylama yapıldı ve sonuçların aşağıdaki gibi olduğu görüldü.
- A > B > C (1/3’ü A’yı B’ye ve yine 1/3’ü B’yi C’ye tercih eder)…..33 oy
- B > C > A (1/3’ü B’yi C’ye ve yine 1/3’ü C’yi A’ya tercih eder)…..33 oy
- C > A > B (1/3’ü C’yi A’ya ve yine 1/3’ü A’yı B’ye tercih eder)…..33 oy
- Bu durumda; 66 seçmen A’yı B’ye tercih ediyor
- 66 seçmen B’yi C’ye tercih ediyor
- 66 seçmen C’yi A’ya tercih ediyor
Dolayısıyla seçmenlerin üçte iki çoğunluğu A’yı B’ye; B’yi C’ye ve C’yi A’ya tercih ediyor. Gördüğünüz gibi ortaya bir paradoksal sonuç çıktı.
Seçim yöntemleri üzerine yapılan araştırmaların günlük yaşam üzerinde bir etkisi oldu mu? Çok değil. Birkaç örnekte, özellikle politika yapıcıların uzmanlara danışma zahmetine katlandıkları durumlarda, tercih edilen yöntemlerin sınırlamalarının dikkate alındığının görülebildiği doğrudur. Ancak çoğu durumda bu böyle değildir.
Ancak yine de bu bulguların önemli bir karşılığı da oldu. Arrow’un yaklaşımı, ideal bir oylama sisteminin karşılaması gereken temel varsayımlar arasındaki potansiyel gerilimi vurgular. Kabul edilebilir oylama sistemleri sağlamak için bunların nasıl değiştirilebileceğini ve bu sistemlerin teorik doğasını keşfetmemizi sağlar.
Sonucunda Condorcet ve Arrow bize oylama sistemlerinin düşündüğümüzden daha karmaşık olduğunu ve oylama sistemlerini matematiksel olarak nasıl analiz edeceğimizi gösterdiler. Arrow’un teoremi, deneyimlerimizden zaten bildiğimiz bir şeye matematiksel destek sağlıyor. Her koşulda makul derecede adil bir sonuç üreten bir sistem tasarlamak gerçekten zordur.
Ayrıca demokrasi söz konusu olduğunda matematik, gerekli olduğu kadar sınırlıdır. İnsanların oy kullanma haklarını kullanmalarını veya kullanabilmelerini engelleyen sosyal ve politik sorunlar hakkında hiçbir şey yapamaz. Konu ile ilgili başka bir yazımız için: Gerrymandering Nedir? Seçimlerde Yapılan Bir Manipülasyonu Geometri Yardımı İle Nasıl Anlayabiliriz?
Kaynaklar ve ileri okumalar:
- Amadae, S.M.. “impossibility theorem”. Encyclopedia Britannica, 15 Jan. 2015, https://www.britannica.com/topic/impossibility-theorem. Accessed 1 September 2024.
- Maths in a minute: Arrow’s theorem; yayınlanma tarihi: 29 Mayıs 2013. Kaynak site: Plus Math. Bağlantı: Maths in a minute: Arrow’s theorem
- Kenneth Arrow’s legacy and why elections can be flawed. Yayınlanma tarihi: 1 Mart 2017. Kaynak site. Conversation. Bağlantı: Kenneth Arrow’s legacy and why elections can be flawed
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





