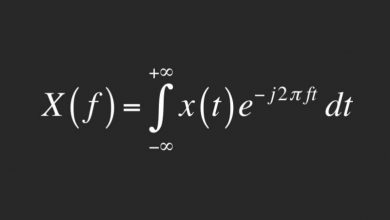Günümüzde faktöriyeller matematiğin her yerinde karşımıza oldukça sık biçimde çıkıyor. Bildiğiniz gibi faktöriyel hesapları negatif olmayan n tamsayıları için, n’den küçük veya ona eşit tüm pozitif tam sayıların çarpımını ifade eder.
Örneğin, 4! = 1 x 2 x 3 x 4 = 24 anlamına gelir. Bu gösterim biçimi de Fransız matematikçi Christian Kramp tarafından 1808’de matematik camiasına tanıtılmıştır. Faktöriyeller, özellikle nesneleri düzenlemenin farklı yollarının sayısını belirlerken önemlidir. Ayrıca sayı teorisi, olasılık ve matematikte de karşımıza sık olarak çıkar.
Faktöriyeller ile ilgili bir sorun sonuçlarının çok hızlı büyümesidir. Buna bir örnek olarak hepimizin aşina olduğu iskambil kağıtlarını verebiliriz. Elinizde 52’lik bir iskambil kağıdı destesi olduğunu ve bunu düzenlemek istediğinizi düşünelim. Bu durumda 52 farklı kart 52!= 52 × 51 × 50 × 49 ×… × 3 × 2 × 1 farklı biçimde düzenlenebilir. Bu çarpımın karşılığı 8.06582 x 1067 kadardır.
52! ne kadar büyük bir sayı olduğunu tarif etmek aslında kolay bir iş değildir. Şu anda hayatta olan tüm insanlar, evren başladığından beri her saniyede bir kart destesi karıştırmış olsaydı, bu sadece 3 × 10 27 karıştırmaya denk gelirdi. Aslında bu sayı da, asıl sayımızla karşılaştırıldığında inanılmaz derecede küçük bir sayı olurdu.
Stirling Formülü Nedir?
52! sayısının yeterince sabrınız ve bir hesap makinanız var ise hesaplanması basittir. Ama bu, hem sıkıcı hem de hata yapmaya açık bir metottur. Bunun yerine İskoç matematikçi James Stirling’in (1692-1770) adını taşıyan herhangi bir faktöriyel hesabının sonucunu yaklaşık olarak bulmamızı sağlayan güzel bir formül kullanabiliriz. Bu formül yerine benzer bir mantıkla Gama fonksiyonunu da kullanabilirsiniz. Detayları burada: Ondalık Sayıların Faktöriyeli Olur mu? Gama Fonksiyonu İle Tanışın
Newton’un yakın arkadaşı olan James Stirling günümüzde 1730 yılında kaleme aldığı Methodus Differentialis isimli kitabı ve soyadını taşıyan Stirling Formülü ile bilinir. Formülü aşağıda görebilirsiniz. Bu formülde n yerine 52 yazdığımızda sonuç 8.0529 x 1067 olacaktır ki bu yazının başlarında verdiğimiz sonuca oldukça yakın bir cevaptır.
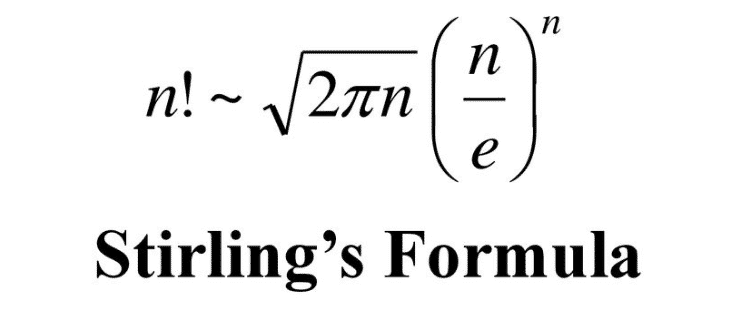
Matematikçe Keith Ball şöyle yazıyor: “Bence bu, on sekizinci yüzyıl matematiğin en önemli keşiflerinden biridir. Bunun gibi bir formül, matematiğin on yedinci ve on sekizinci yüzyıllarda meydana gelen şaşırtıcı dönüşümü hakkında bize bir fikir verir.
Logaritmalar, 1600’lere kadar icat edilmedi. 90 yıl sonra, Kalkülüsün ilkelerini belirleyen Newton’un Principia’sı ortaya çıktı. Devamında matematikçiler Stirling formülü gibi, formüller üretiyorlardı. Matematik artık amatörler için bir oyun değildi – profesyoneller için bir iş haline gelmişti.”
Bir Deste İskambil Kağıdını Rasgele Dağıtmak İçin Kaç Karıştırma Gerekir?
Hazır iskambil kağıtlarından bahsetmişken konuya devam edelim. Varsayımlar yaparak, belirli bir düzenin evrenin yaşamı boyunca asla iki kez gerçekleşmeyeceğini iddia etmek kolaydır. Ancak burada büyük bir şart var.
Gerçek rastgeleliği sağlamak için kartların karıştırılması yeterince kapsamlı olmalıdır. Bu noktada düşünmek gerekir. Rastgelelik nedir ve tamamen rastgele olan bir şeye sahip olmak mümkün müdür? Rastgelelik veya tamamen öngörülemezlik kavramını neredeyse medeniyet kadar uzun süredir tartışıyoruz.
1992’de Bayer ve Diaconis, 52 kartlık bir destenin riffle shuffle denilen yöntemle yedi rastgele karıştırılmasından sonra, her dizilimin neredeyse eşit derecede olası olduğunu gösterdi. Bunun anlamı şudur. Krupiye, karıştırmayı hata yapmadan yapabilirse iskambil kağıtları sadece sekiz mükemmel karıştırma işleminden sonra ambalajlarından ilk çıktıkları zamandaki sıralamasına geri dönebilir.
Ancak bu sonucun mümkün olabilmesi için yukarıdaki videoda gözlemlediğiniz gibi bu işte gerçekten işinizin ehli olmanız gerekmektedir. Bu nedenle kumarhanelerde iskambil kağıdı karıştırılırken kartlar masanın üzerine yayılır ve kuralsız biçimde karıştırılır.
Bu arada aşağıdaki videoda göreceğiniz overhand shuffle denilen yöntem ise, kartları karıştırmanın gerçekten kötü bir yoludur: 52 kartlık bir desteyi rastgele dağıtmak için yaklaşık 2500 bunu yapmanız gerekir. Yazının devamında göz atmak isterseniz: Çay Yaprağı Paradoksu: Çay Çöpleri Neden Bardağın Ortasında Toplanır?
Kaynaklar ve ileri okumalar:
- Stirling’s formula; Bağlantı: https://www.britannica.com
- Seven Shuffles; Bağlantı: https://math.hmc.edu
- What is the purpose of Stirling’s approximation to a factorial?; bağlantı: https://math.stackexchange.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel
