Ondalık bir sayının faktöriyeli nedir? sorusu faktöriyellerin tanımı nedeniyle kulağa saçma gelir. Oysa ki gama fonksiyonu sayesinde bunu hesaplamak mümkündür. Örneğin 2,5! yaklaşık olarak 1,329 değerine eşittir. 1,5! ise yaklaşık olarak 0,886 kadardır. Peki ama nasıl sorusunun cevabı için okumaya devam ediniz.

Faktöriyel Nedir?
Elinizde bir alışveriş listesi, ya da bir isim listesi herhangi bir liste olsun. Siz de bunu düzenlemek isteyin. Liste A ve B gibi iki sembol içeriyorsa, bunun için iki yol vardır: AB ve BA. Liste üç harf A, B ve C içeriyorsa, altı yol vardır: ABC, ACB, BAC, BCA, CAB, CBA. Ya dört harf A, B, C ve D içeriyorsa? Tüm olasılıkları sistematik olarak yazabilirsiniz ve yanıt 24 olur.
Peki 5 harf ABCDE’yi düzenlemenin kaç yolu var? Aynı mantıkla cevap elbette 5 × 24 yani 120 olacaktır. Bu da bizi durumu bir kurala bağlayan faktöriyeller ile tanıştırır.

Aynı mantıkla, n harfi yeniden düzenlemenin farklı yollarının sayısı ise n × (n – 1) × (n – 2) ×… × 3 × 2 × 1 biçimindeki çarpım için “n faktöriyel” ifadesini kullanır ve n! olarak yazılır. Bu kısaca 1’den n’ye kadar olan tüm sayıların çarpımıdır.
52 oyun kartından oluşan bir iskambil destesini sırayla düzenlemenin farklı yollarının sayısı: 52! = 80 658 175 170 943 878 571 660 636 856 403, 766 975 289 505 440 883 277 824 000 000 000 000. Peki ama tüm bunları zaten biliyordum diyorsanız devam edelim. Çünkü ortaöğretim sıralarında tanıştığımız bu gösterim biçimi aslında işin sadece başlangıcıdır. Faktöriyeller genel olarak Gama Fonksiyonu ile de tanımlanır. Bu fonksiyonun formülünü aşağıda görebiliyorsunuz.
Gama Fonksiyonu Nedir?
Gama fonksiyonu matematikte faktöriyel fonksiyonunun karmaşık sayılar ve tam sayı olmayan reel sayılar için genelleyen bir fonksiyondur. Bu tuhaf görünümlü fonksiyonu, Yunan alfabesinden büyük harf gamma ile şuna benzer Γ(z) bir biçimde yazarız. Bu fonksiyon ilk defa 1729 yılında matematikçi Leonhard Euler tarafından keşfedilmiştir.
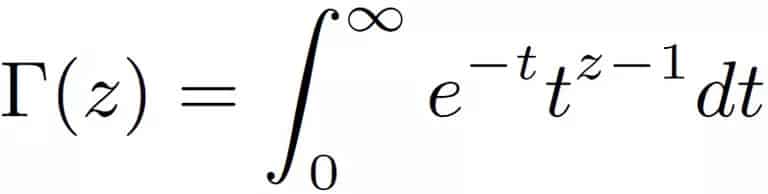
Matematik kariyerimizin en başında faktöriyellerin negatif olmayan tamsayılar için tanımlandığını öğreniyoruz. Şimdi bunu bir fonksiyon mantığı ile ele alalım ve listemizi oluşturalım. (n, n!)= (0, 1), (1, 1), (2, 2), (3, 6), (4, 24), (5, 120), (6, 720)… biçiminde bir sonuç elde ediyoruz. Bu noktaları kartezyen sistemde işaretledikten sonra bazı meraklı beyinlerin aklına şöyle bir soru gelir. Noktaları birleştirip grafiği tamamlamanın bir yolu var mıdır? Evet vardır ve bu noktada Gama fonksiyonu işin içine karışır.
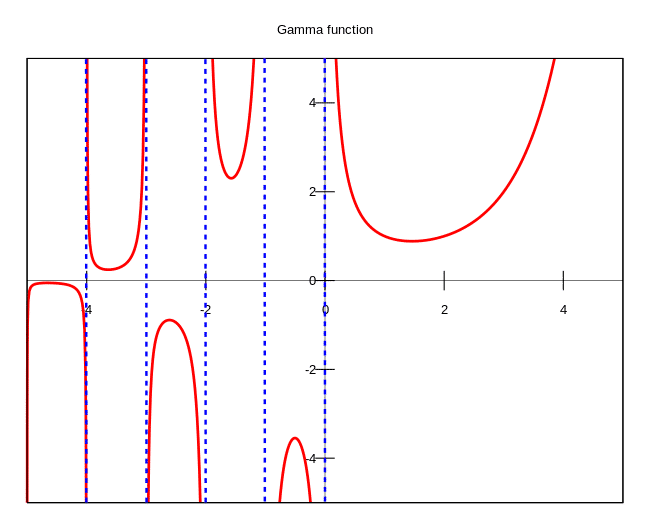
Gama fonksiyonu yardımı ile sayılar ile ilgili bazı özellikleri tanımlarız. Bunlardan bir tanesi Γ (z + 1) = z Γ (z) biçimindedir. Yukarıdaki formül, faktöriyel ve gama fonksiyonu arasındaki bağlantıyı kurar. Bu bağlantı pozitif n tamsayısı için, Γ (n) = ( n-1)! kuralı aracılığıyla kurulur. Bu da bize sıfır faktöriyel değerinin neden 1’e eşit olduğunun cevabını verir.
Gama fonksiyonu z’nin negatif tamsayı değerleri için sonsuz ve diğer tüm karmaşık sayılar için sonludur. İstatistikte önemli uygulamaları vardır. Faktöriyeli tanımlayan anahtar özelliğe sahiptir. Gama fonksiyonu ile uğraşarak ilginç bazı sonuçlara da erişebilirsiniz. En iyi bilinen (ve şaşırtıcı) sonuçlardan biri Γ (1/2) = √π olmasıdır. Γ (n) = ( n-1)! olduğundan buradan da (-1/2)!= √π gibi bir sonuç elde ederiz ki bu sonuç gerçekten ilk bakışta oldukça şaşırtıcıdır.
Gama Fonksiyonu Ne İşe Yarar?
Bu fonksiyon matematiğin görünüşte alakasız birçok alanında ortaya çıkar. Özellikle, faktöriyel genellemesi bazı olasılık problemlerinde bize yardımcı olur. Örneğin, gama dağılımı, gama fonksiyonu cinsinden ifade edilir. Bu dağılım, depremler arasındaki zaman aralığını modellemek için kullanılır. Ayrıca, Gama fonksiyonunun özel bir hali olan Erlang, iletişim teknolojisinde sıklıkla karşımıza çıkan olasılık hesaplarında yer alır.
Google arama motorlarında alınan bazı kararlar, politikada oy hesapları, kişilere özel etkin reklam tasarımı gibi konuların arkasındaki matematiksel çalışmalarda Gama’nın yine özel bir hali olan K-Kare (Chi-square) kendini gösterir. Yani siz fark etseniz de etmeseniz de matematik bir biçimde arka planda çalışmaya devam etmektedir.
Kaynaklar ve ileri okumalar:
- What Is the Gamma Function?; Yayınlanma tarihi: 4 Şubat 2018; Bağlantı: https://www.thoughtco.com
- Britannica, The Editors of Encyclopaedia. “gamma function”. Encyclopedia Britannica, 13 Oct. 2023, https://www.britannica.com/science/gamma-function. Accessed 14 January 2024.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










