Matematikte bazı kavramları genellikle ezberler, nedenini tam bilmeden kullanırız. Bu duruma faktöriyel konusu da güzel bir örnektir. Özellikle sıfır faktöriyel ifadesiyle ilk kez karşılaştığımızda, “0! = 1” olduğu söylenir ve ardından örneklerle konuya devam edilir. Ancak çoğu zaman öğrencilerin aklındaki en doğal soru yanıtsız kalır: Peki ama neden sıfır faktöriyel bire eşittir?

Pek çok matematiksel hesaplamada karşımıza çıkan faktöriyeller, n doğal sayıları için, n’den küçük veya ona eşit tüm sayıların çarpımını ifade eder. Örneğin, 4! = 24 dendiğinde, 4 x 3 x 2 x 1 = 24 işleminin yapıldığını anlarız. Tanım gereği, 0! = 1 ve 1! = 1 olarak kabul edilir.
Bu tanımda kafa karıştıran nokta, sıfır faktöriyelin bire eşit olduğunu belirten ifadedir. 0 faktöriyel, içinde değer bulunmayan bir veri kümesini düzenleme yollarının sayısını bulmak anlamına gelir. Peki ama neden bu sonucun bir olduğu kabul edilir?
Faktöriyellerin Genellemesi Gama Fonksiyonu İle Tanışalım
Ortaöğretim sıralarında tanıştığımız faktöriyel gösterimi aslında işin sadece başlangıcıdır. Aşağıdaki görselde Gama fonksiyonunu görüyorsunuz. “Sıfır faktöriyel neden bire eşittir?” sorusunun asıl cevabı bu fonksiyonda saklıdır.
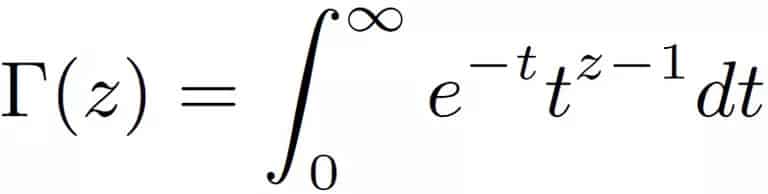
Gama fonksiyonu, matematikte faktöriyel fonksiyonunu karmaşık sayılar ve tamsayı olmayan reel sayılar için genelleyen bir fonksiyondur. Bu fonksiyon, Yunan alfabesindeki büyük gamma harfiyle, Γ(z) biçiminde gösterilir. İlk kez 1729 yılında matematikçi Leonhard Euler tarafından tanımlanmıştır.
Gama fonksiyonunun bazı temel özellikleri vardır. Bunlardan biri Γ(z + 1) = z·Γ(z) eşitliğidir. Ayrıca Γ(1) = 1 kabulü de yapılır. Bu iki özellik birlikte kullanıldığında:
Γ(z) = (z – 1)·Γ(z – 1) = (z – 1)(z – 2)·Γ(z – 2) = … = (n – 1)! ifadesine ulaşılır. Bu bağlantı, gama fonksiyonu ile faktöriyel kavramı arasında doğrudan bir ilişki kurar. Bu da Γ(1) = (1 – 1)! = 0! sonucunu verir. Yani sıfır faktöriyel değerinin neden 1’e eşit olduğu sorusunun temel cevabı burada yatar.
Ayrıca gama fonksiyonu, ondalık sayıların faktöriyelini de tanımlamaya olanak sağlar. Örneğin 2,5! yaklaşık olarak 1,329; 1,5! ise yaklaşık olarak 0,886 değerindedir. Bu da faktöriyelin yalnızca doğal sayılarla sınırlı kalmadığını gösterir.
Sıfır Faktöriyel Nedir?
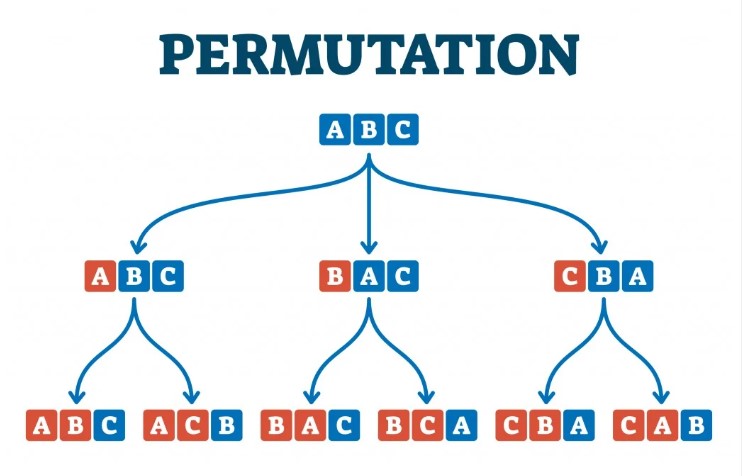
Yukarıda aktardığımız Gama fonksiyonu, sıfır faktöriyel konusuna matematiksel bir açıklama getirir. Ancak bu yaklaşım sezgisel değildir ve temel seviyedeki bir öğrenciye bu yolla açıklama yapmak kolay olmayabilir. Bu nedenle şimdi konuyu daha farklı bir bakış açısıyla değerlendirelim. Bilindiği gibi faktöriyel, permütasyon ve kombinasyon konularının temelini oluşturur.
n! ifadesi, n tane farklı nesneyi kaç farklı şekilde sıralayabileceğimizi belirtir. Örneğin, üç farklı gömleğiniz varsa bunları bir rafa sıralamak için 3! = 6 farklı yolunuz vardır. Gömlek sayınız iki olduğunda ise bu sayı 2! = 2 olacaktır. Eğer sadece bir gömleğiniz varsa, onu sadece olduğu gibi bırakabilirsiniz. Yani 1! = 1 olur.
Peki hiç gömleğiniz yoksa? Burada işin içine biraz düşünsel bir boyut girer. “Hiç gömleğim yok, bunu kaç farklı biçimde sıralayabilirim?” sorusuna sezgisel olarak “hiçbir şekilde” yanıtını verebilirsiniz. Ancak matematikte bu durum, boş küme ile ifade edilir. Boş kümenin de tek bir düzenlenme biçimi vardır: hiçbir şey yapmamak. Bu da matematiksel olarak bir şekilde yorumlanır. Yani 0! = 1 tanımı, bu sezgisel düşünceyle de desteklenmiş olur.
Sıfır faktöriyel neden Bir Yapar sorusunun İkinci Olası cevabı
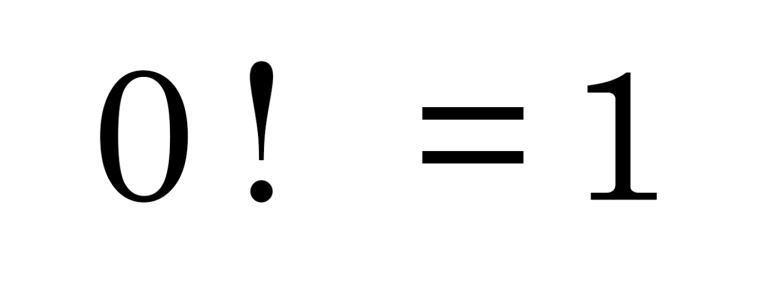
Sıfır faktöriyelin 1 olarak kabul edilmesi, matematiksel işlemlerin ve denklemlerin tutarlı bir şekilde işlemesine de yardımcı olur. Birazdan göstereceğimiz yöntem, size sıfır faktöriyelin neden bir olduğunu açıklamaz. Ancak neden bu biçimde kabul edilmesi gerektiği konusunda bir fikir verir.
Kombinasyon, öğelerin sıraya bakılmaksızın gruplandırılmasıdır. Örneğin {1, 2, 3} kümesini ele alalım. Bu elemanları hangi sırayla seçersek seçelim, sonuçta aynı üçlü grubu elde ederiz. Bu nedenle kombinasyon hesaplamalarında C(n, r) = n! / [r!(n – r)!] formülü kullanılır.
Eğer 3 elemanlı bir kümenin 3’lü kombinasyonlarını hesaplamak istersek, paydanın bir bölümünde (3 – 3)! ifadesi yer alır. Bu da doğrudan 0! = 1 kabulünü kullanmamızı gerektirir.
Sonuç olarak, 0 faktöriyelin 1 olmasının temel nedeni, bunun bir matematiksel kabul olmasıdır. Bu kabul, birçok denklem ve özdeşliğin tutarlılığını korumamıza yardımcı olur.. Yazımızın devamında okumaya devam etmek isterseniz: Verilen Bir Sayıyı Neden Sıfıra Bölemiyoruz?
Kaynaklar ve ileri Okumalar:
- Taylor, Courtney. “Why Does Zero Factorial Equal One?” ThoughtCo, Apr. 5, 2023, thoughtco.com/why-does-zero-factorial-equal-one-3126598.
- Why Is The Factorial Of Zero Equal To One?. Yayınlanma tarihi: 8 Temmuz 2022. Bağlantı: Why Is The Factorial Of Zero Equal To One?
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel