Brown Hareketi Nedir? Sıvılar ile Borsanın Ne İlgisi Vardır?

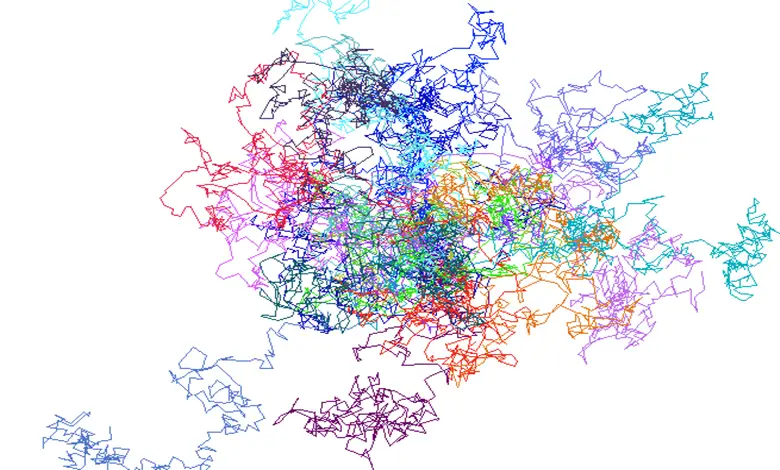
Bilimde rastgele olayları tanımlamak kolay değildir. Ancak yine de bu tip olayları olasılık teorisi ile matematiksel olarak tanımlamanın bir yolunu biliyoruz. Bunun içinde elimizde iki güçlü silahımız var. Bunlardan biri simetri diğeri ise evrensellik. Simetri fikrini açıklamak kolaydır, ancak evrensellik biraz daha incelikli bir anlayış gerektirmektedir. Evrensellik fikri ile ilgili güzel bir örnek Brown hareketi olacaktır.

İki farklı sıvıdaki moleküllere mikroskobik olarak bakarsanız, çok farklı göründüklerini fark edersiniz. Bununla birlikte, iki sıvının büyük ölçeklerde nasıl davrandığına bakarsanız, benzer davranışlar görürsünüz. Aslına bakarsanız tüm akışkanların davranışı sadece birkaç parametreye sahip olan bir matematiksel modelle tanımlanabilmektedir.

Brown Hareketi Nedir ve Nasıl Keşfedilmiştir?

Brown hareketi, adını botanikçi Robert Brown’dan (21 Aralık 1773 -10 Nisan 1858) almıştır. Kendisi güney yarımkürede geçirdiği zaman boyunca Avustralya’ya özgü 4000 bitki türünü sı­nıflandırmıştır. Aynı zamanda hücre çekirdeğine Latince’de küçük tohum, öz manasına gelen nucula’dan türettiği nucleus adını veren kişidir.

Fakat Brown esas olarak, 1827 yılında suda asılı polen tanecikleri üzerine yaptığı gözlemle tanınır. Büyütecinin ardındaki Brown, sudaki taneciklerin, zikzaklar çizerek heyecanlı bir hareket içinde olduğunu gözlemlemiştir. Ne yazık ki kendisi asi polen taneciklerinin sırrını hiçbir zaman çözemedi. Bu konudaki asıl ilerleme için, 26 yaşındaki Albert Einstein’ı beklemek zorunday­dık.

Einstein İle Brown Hareketinin İlgisi Nedir?

Fizikte yeni bir çağın doğuşunu müjdeleyen dönüm noktası, 1905 ‘te bir dizi bildirinin Alman fizik dergisi Anna­len der Physik’te yayınlanması oldu. Çalışmayı yayınlayan kişinin Adı Albert Einstein’dı. Kendisi son derece faal geçen bir tek sene içinde beş bildiri sunmuştu. Bu bildirilerden bir tanesi de Brown hareketini incelemekteydi.

Günümüzde atomların varlığı hepimize küçüklüğümüzden beri anlatıldığı için doğal gelir. Fakat 1900 yılında, bilim camiasında atomların var olup olmadığı tartışmalı bir konuydu. Fotoğraf, telefon ve radyo yeni bir teknoloji çağının başlangıcını müjdelemişti ama maddenin neden yapıldığı konusunda bir fikir birliği yoktu.

Einstein’ı en çok zaman ve uzayla ilgili çalışmalarından, bir de genel ve özel görelilik kuramlarından biliriz. Fakat doktora tezinin konusu, sıvıların istatistiksel moleküler kuramıydı. 1905 ve 1908′ de yayımladığı makalelerinde Brown hareketinin de sağlam matematiksel bir açıklamasını ortaya koymuştu. Einstein’ a göre polen taneciklerinin çılgınca dansının nedeni, küçük su molekülleri tarafından sürekli bir bom­bardımana maruz kalıyor olmalarıydı. Bunu basit bir örnekle anlayabilirsiniz.

İnsan boyunu aşan bir şişme topun geniş bir alanda birçok kişi tarafından itildiğini düşünün. Bu durumda top dengesiz ve düzensiz hareketler yapacaktır. Sonucunda herkesin itme gücü birbirinden farklıdır. Benzer şekilde, polen taneciğinin düzensiz hareketlerinin nedeni de, polenin bir tarafına kıyasla bir diğer tarafında daha çok su molekülü baskısı olmasıdır.

Brown hareketi rastgeledir. Bu mikropartiküllerden birinin konumunu bir andan diğerine kesin olarak tahmin edemezsiniz. Ancak bir parçacığın nereye hareket edebileceğini tanımlayan bir olasılık dağılımı atayabilirsiniz. 

Einstein ve adı pek de bilinmeyen fizikçi Marian Smoluchowski bu olasılık dağılımının zaman içinde nasıl değiştiğinin, ısının nesnelerin içinden akma şeklini tanımlayan aynı matematik tarafından tanımlandığını fark eden ilk kişilerdir. Teori 1908’de Jean Perrin tarafından da deneysel olarak doğrulandı. Aslında bu doğrulama atomların varlığı ile ilgili tartışmalara da bir son verdi.

Brown Hareketi Neden Önemlidir? Ne İşe Yarar?

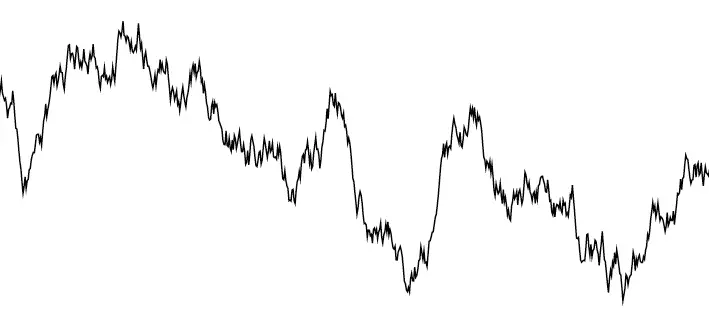
Brown hareketi evrenseldir. Parçacıkların ve ilgili sıvı moleküllerinin belirli şekillerinin altında yatan ayrıntılardan bağımsız olarak birçok mikro parçacığın rastgele hareketinde ortaya çıkar.

Aslına bakarsanız Brown hareketi ilk olarak 1900 yılında finansal sistemler üzerinde çalışırken Fransız matematikçi Louis Bachelier tarafından matematiksel olarak tanımlanmıştı. Louis Bachelier, 1900 yılında borsanın stokastik analizi üzerine bir doktora tezi hazırlamış ve Spekülasyonların Teorisi adlı bir model geliştirmiştir. Bachelier, hisse senedi fiyatlarının evrimini, gerçekleşen sayısız ticaretten kaynaklanan fiyattaki küçük yukarı ve aşağı itmelerin birikimi olarak tanımlamıştı.

Polen mikropartiküllerinin hareketi gibi, hisse senedi fiyatlarının evrimini de tam olarak tahmin etmek imkansızdır. Ancak bir hisse senedi fiyatının değerinin nasıl değişeceğini açıklayan bir olasılık dağılımı atayabiliriz.

Brown hareketinin keşfinin öyküsü ve evrenselliği, matematiğin karmaşık olayları olasılıkları kullanarak tanımlama gücünü gösterir. Aynı zamanda matematik ve fiziğin bütünlüğünün güzel bir örneğidir.  

Bugün, Brown hareketini tanımlayan matematiksel modeller matematik, ekonomi, mühendislik, fizik, biyoloji, kimya ve diğer birçok disiplinde kullanılmaktadır. Yazının devamında göz atmak isterseniz: Mikro Evrenden Makro Evrene: İstatistiksel Mekanik Nedir?

Kaynaklar ve ileri okumalar

• An Introduction to Brownian Motion. Yayınlanma tarihi: 6 Haziran 2019; Bağlantı: https://www.thoughtco.com
• The maths of randomness: universality. Yayınlanma tarihi: 19 Nisan 2018; Bağlantı: https://plus.maths.org/

Size Bir Mesajımız Var!

Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel