Veri bilimi konusunda eğitim almayı düşünüyorsanız ancak içerdiği matematik konusunda bazı endişeleriniz varsa okumaya devam edin. Veri bilimi ile matematik ilişkisi düşünülenden çok daha fazladır.
İnsanlığın kaydettiği bilgi miktarı baş döndürücü bir hızla artıyor. Günümüzde yeni bilgilerin neredeyse tümünü dijital ortamda, bilgisayarların okuyabileceği biçimde üretiyoruz. Yaptığınız alışverişler, Google aramalarınız, iletişiminizin tümü, cebinizde telefonunuzla saat kaçta nereye kaç adım atarak gittiğiniz, bir web sitesini incelerken imleci ekranın neresinde kaç saniye tuttuğunuz, tüm sağlık bilgileriniz, hepsi kayıt altında. İstatistik bilimiyle büyük veri işleme gücünü birleştiren veri biliminin dünyasına hoş geldiniz.
Detaylara geçmeden önce hatırlatalım. Veri bilimi yeni bir tanımlamadır. Veri bilimi bir zamanlar bilgisayar bilimi ile eş anlamlı olarak kullanılıyordu. 2001 yılında William S. Cleveland bağımsız bir disipline ithafen ilk kez “veri bilimi” terimini kullandı. Harvard Business Review ise, 2012’de veri bilimcisinin rolünü “21. yüzyılın en seksi işi” olarak tanımlayan bir makale yayınladı. Önce kısa bir tanım verelim.
Veri Bilimi Nedir?

Veri bilimi, büyük miktardaki verileri analiz ederek anlamlı bilgiler elde etmeye odaklanan bir disiplindir. Veri bilimcileri, karmaşık veri setleri arasındaki desenleri, eğilimleri ve ilişkileri keşfetmeye çalışır. Devamında da bu bilgileri işletmelere, kuruluşlara veya diğer alanlara iç görüler sunmak için kullanır. Yaşadığınız yer, bir veri analisti olarak ne kadar kazanacağınız üzerinde büyük bir etkiye sahiptir. Ancak bu sektörde bir kariyer yapmak ortalamanın üstünde maaş kazanabileceğiniz anlamına gelir.
Durum böyle olunca da bir veri bilimcisi olmak istemeniz mantıklıdır. Ancak bu noktada akılda tutulması gereken şey veri biliminin tüm gücünü matematikten aldığıdır. Veri bilimi kabaca istatistik ve matematik ile bilgisayar bilimlerinin kesişimi olarak düşünülmelidir. Bu nedenle de veri bilimi ile uğraşmak isteyen bir kişinin öncelikle matematiği detaylıca öğrenmesi gerekmektedir. Durum böyle olunca da iyi bir veri bilimcisi olmak kolay değildir.
Veri Bilimi Hangi Matematik Konularını İçerir?
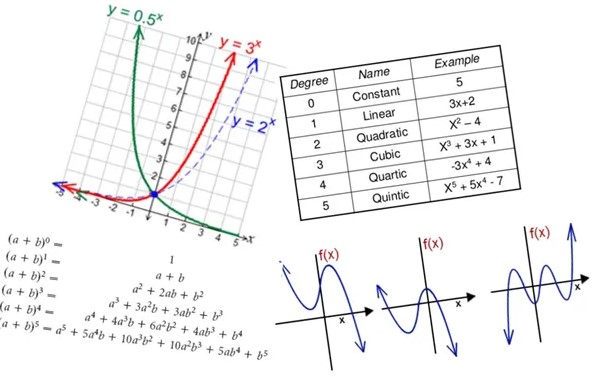
Veri bilimi ile matematik arasında birazdan size aktaracaklarımız kesinlikle detaylı olmayan kısa bir listedir. Bu çalışmalarda yer edinen matematik ve bilgisayar biliminin başka birçok alanı vardır. Önce işin temeli ile başlayalım.
Lineer Cebir: Makine Öğreniminin Omurgası
Günümüzde her türlü veri genellikle diziler ve matrisler olarak temsil edilmektedir. İster basit bir Excel sayfasına, ister karmaşık bir ağ yapısına bakıyor olun, esasen matrislere bakıyorsunuzdur. Doğrusal cebir ya da lineer cebir; matematiğin, vektörler, vektör uzayları, doğrusal dönüşümler, doğrusal denklem takımları ve matrisleri inceleyen alanıdır. Özellikle makine öğrenmesi ve veri bilimi alanında kullanılmaktadır. Matrisleri işlemek için araçlar sunarak verileri anladığımız dil haline getirmeye aracı olur.

Büyük veri çağında verimlilik yalnızca bir lüks değildir bir zorunluluktur. Doğrusal cebir, özellikle optimizasyon teknikleriyle birleştirildiğinde, verimli hesaplamaya olanak tanır. Büyük veri kümeleri üzerindeki işlemlerin hem hızlı hem de doğru olmasını sağlar.
Birçok algoritmanın temelinde doğrusal denklem sistemlerini çözme ihtiyacı yatmaktadır. Lineer cebir ise bunu etkili bir şekilde yapmanız için gereken araçları sağlar. Kısacası Lineer cebir sizi makine öğreniminin tüm gücünden yararlanma becerileriyle donatır. Bu sayede algoritmaları yalnızca kullanmak yerine nasıl işlediklerini de anlarsınız.
Kalkülüs: Değişimi Anlamak
Eğer lineer cebir verinin diliyse, kalkülüs de değişimin dilidir. Özünde bize olayların nasıl ve hangi oranda değiştiğini anlamamız için gerekli araçları sağlar. Bu, veri bilimi ve makine öğrenimi için son derece önemli bir katkıdır. Sonucunda ister zaman içindeki hisse senedi fiyatlarını takip etmek, ister bir uygulamadaki kullanıcı davranışını analiz etmek, ister gelecekteki satışları tahmin etmek olsun, her şey değişimi anlamak ve tahmin etmekle ilgilidir.

Bir virüsün yayılması, bir popülasyonun büyümesi veya bir maddenin bozulması gibi birçok gerçek dünya olgusu, temel bir temel olan diferansiyel denklemler kullanılarak modellenir. Bu denklemleri çözerek gelecekteki durumları tahmin eder veya altta yatan dinamikleri anlarız.
Neredeyse her makine öğrenmesi algoritması, çeşitli kısıtlamaları tabi olan bir tür tahmin hatasını en aza indirmeyi amaçlar. Bu ise bir optimizasyon problemidir. Optimizasyon, bir sistemin veya sürecin en iyi sonuçları elde etmek için tasarlanması, ayarlanması veya iyileştirilmesi işlemidir.
Veri biliminde bu genellikle parametrelerin ayarlanması, algoritmaların iyileştirilmesi veya modellerin en üst düzeyde performans göstermesini sağlamak için en alakalı özelliklerin seçilmesi anlamına gelir. Lojistik şirketleri için teslimat rotalarının optimize edilmesinden akış platformlarındaki önerilere ince ayar yapılmasına kadar, veri biliminde optimizasyon uygulamaları oldukça fazladır. Verimlilik ve hassasiyetin çok önemli olduğu veri biliminin dinamik dünyasında optimizasyon, yol gösterici yıldız görevi görür.
Olasılık ve İstatistik: Veriyi Anlamlandırmak

Olasılık ve istatistiklerin yol gösterici ışığı olmadan veri bilimi anlamlı sonuçlara ulaşamaz. Hayat, verilerde olduğu gibi belirsizliklerle doludur. Olasılık bize bu belirsizliği anlamak ve ölçmek için bir çerçeve sağlar. Geleneksel istatistikler genellikle sabit olasılıklara odaklanırken Bayes istatistikleri, yeni veriler geldikçe bu olasılıkların güncellenmesine olanak tanır. Bu dinamik düşünme biçimi, algoritmaların kullanıldığı makine öğrenimi gibi alanlarda özellikle değerlidir.

Veri analizinin derinliklerine dalmadan önce, bilgi edinmek çok önemlidir. Ortalama, medyan, mod, varyans ve standart sapma gibi ölçümleri içeren tanımlayıcı istatistikler verilerinizin anlık görüntüsünü sunar.
Yeni bir pazarlama stratejisinin satışları artırıp artırmadığını, ya da bir ilacın önemli bir etkisinin olup olmadığını belirlemek istediğinizi düşünün. Bu noktada hipotez testi yapmanız gerekecektir. Hipotez testi, bir hipotezin doğruluğunun istatistiksel bir güvenilirlik aralığında saptanması için kullanılan yöntemdir. Bu aşamadan sonra da tahminlerde bulunmanız gerekecektir. Güven aralıkları ile bir tahminden ne kadar emin olduğunuzu ifade edebilirsiniz.
Veriler nadiren eşit şekilde dağıtılır. Normal, binom veya Poisson dağılımları gibi farklı veri dağılımlarını anlamak, kalıplar ve anormallikler hakkında fikir verecektir. Son olarak istatistikte temel bir kavram olan korelasyon ve nedensellik arasındaki farkı anlamak, verilerinizden anlamlı ve doğru sonuçlar çıkarmanızı sağlar.
Ayrık Matematik: Algoritmalar ve Yapılar
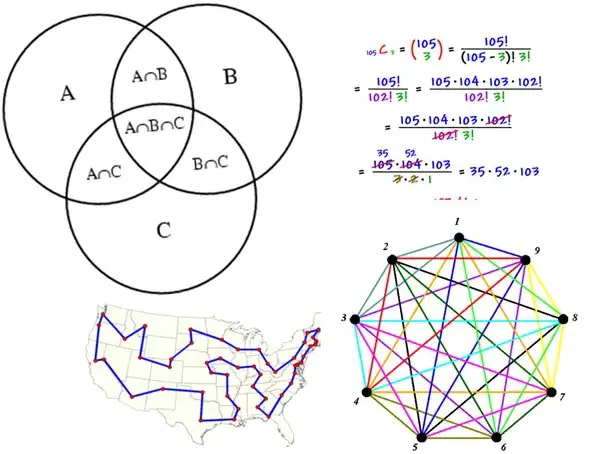
Ağlar her yerdedir; sosyal ağlar, ulaşım sistemleri veya internetin kendisi buna örnektir. Ayrık matematiğin temel direği olan graf teorisi, bu karmaşık ağlara ilişkin bilgiler sunarak ilişkilerin, bağlantıların ve akışın analiz edilmesine yardımcı olur.
Önermeler mantığı gibi kavramlar size sistematik akıl yürütme için bir çerçeve sunarak algoritmalarınızın yalnızca çalışmasını değil aynı zamanda ideal olmasını sağlar. Veriler genellikle farklı kategorilere veya gruplara ayrılır. Küme teorisi bu kategorileri, ilişkilerini ve işlemlerini incelemenin bir yoludur. Permütasyonlar, kombinasyonlar ve verilerin düzenlenmesiyle uğraşırken kombinatorik devreye girer. Özellikle olasılık ve istatistik alanlarında kullanışlıdır ve olası sonuçların ve bunların olasılıklarının belirlenmesine yardımcı olur.
Bilgisayar biliminde temel bir kavram olan özyineleme, temelini ayrık matematikte bulur. Ağaçlar ve fraktallar gibi özyinelemeli algoritmalar ve yapılar, karmaşık sorunları daha basit birimlere bölerek etkili çözümlere olanak tanır. Kısacası ayrık matematik, özünde karmaşık algoritma mimarilerinin ve veri yapılarının inşa edildiği iskeledir. Veri biliminin çok yönlü alanlarında gezinmek için gereken netliği ve hassasiyeti sunar.
Sonuç olarak
Bu yazıda size buzdağının sadece görünen kısmını aktarmaya çalıştık. Veri bilimi ile matematik ilişkisi bundan çok daha fazlasıdır. Sonuçta veri bilimi geleceğin bilimidir. Bu nedenle bu alana dahil olmak ya da en azından olan biteni anlamak için matematik bilmek bir zorunluluktur.
Kaynaklar ve ileri okumalar
- Essential Math for Data Science; Yayınlanma tarihi: 9 Ağustos 2018; Bağlantı: Essential Math for Data Science
- N. Gürsakal, E. Özkan. “Veri Bilim Eğitimi Nasıl Olmalıdır?”. 1st International Data Science & Engineering Symposium (IDSES’19), 2-3 Mayıs 2019, Safranbolu, Karabük,
- Data Science: Overview, History and FAQs. Yayınlanma tarihi: 28 Kasım 2022. Bağlantı: Data Science: Overview, History and FAQs
Matematiksel










