Matrisler Nedir Ve Neden Matematikçiler İçin Çok Önemlidir?

Doğrusal cebir matematiğin en güçlü araçlarından biridir. Doğrusal cebirden bahsedildiği zamanlarda da akla ilk olarak matrisler gelir.Peki ama matris nedir? Ve daha da önemlisi ne işe yarar?

Matris Nedir?

Matrisler aslında satır ve sütunlar halinde düzenlenmiş bir sayı dizisidir. Sayılara matrisin elemanları denir ve yerlerini satırlar ve sütunlar aracılığı ile gösteririz. Aşağıdaki örnek sadece 6 eleman içerirken çok daha büyük veri grupları ile işlemler yapmak zorunda kalabiliriz.

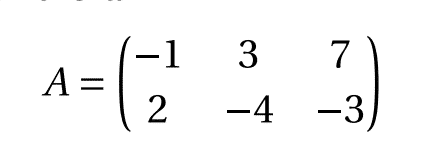
Bir matristeki sayılar verileri temsil edebilir. Örneğin satırlar sıcaklığı, hava basıncını ve nemi, sütunlar bu üç ölçümün yapıldığı farklı yerleri gösteriyor olabilir. Ancak matrisler aynı zamanda matematiksel denklemler için de kullanılır. Örneğin t + 2p + 3h ve 4t + 5p + 6h ifadeleri sıcaklık, basınç ve nem ölçümlerini içeren iki farklı matematiksel işlemi tanımlıyorsa bunları [1 2 3] ve [4 5 6] biçiminde de gösterebiliriz.

Matrisler başlangıçta hepimizin aşina olduğu doğrusal denklem sistemlerini tanımlamanın bir yolu olarak ortaya çıkmıştır. Örneğin x – 2y = 0 ve x – y = 1 denklemlerinin çözümü x= 2 ve y = 1 biçimindedir. (2,1) iki denklemin grafiklerinin kesiştiği noktadır. Bu iki denklem için ilgili matrisi, değişkenlerin katsayılarına karşılık gelecek biçimde [1 -2] ve [1 -1] olarak yazmak mümkündür.

Matrisler günümüzde görüntü işlemeden genetik analize kadar bir çok yerde karşımıza çıksalar da, aslında kullanımları modern zamana özgü değildir. Sayıların bu biçimde dizilmesinin bilinen en eski örnekleri Antik Maya uygarlığına aittir. Onların kullanım amaçları net olmasa da bu sayı diziliş biçiminin matematiksel amaçlar için kullanımına dair ilk örnekler de Antik Çin’den gelir.

1850’de İngiliz matematikçi James Joseph Sylvester bir dizi sayıyı tarif etmek için “matrisler” terimini ilk kullanan kişidir. Sylvester bu terimi tanıttıktan kısa zaman sonra, arkadaşı ve matematikçi Arthur Cayley, matrislerle işlem yapmanın kurallarını formüle etmiş ve matris cebrinin kurallarının standart cebirdekilerden farklı olduğunu göstermiştir.

Gündelik Hayatımızda Matrisler Ne İşe Yarar?

Matrisler matematikte doğrusal dönüşümleri temsil etmek için kullanılır. Lineer dönüşüm veya lineer transformasyon diye de bilinen doğrusal dönüşüm bir vektör uzayındaki vektörleri başka bir vektör uzayındaki vektörlere dönüştüren matematiksel bir işlemdir. Doğrusal cebir, vektörler üzerinde gerçekleştirilen basit dönüşümlerin incelenmesidir.

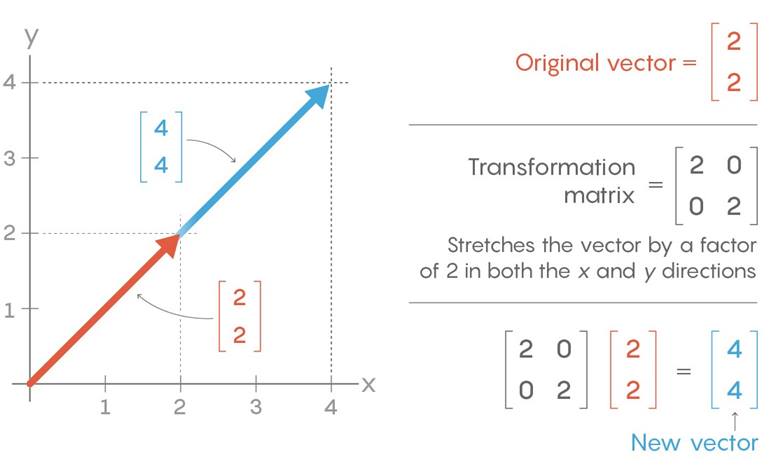
Bu dönüşüm işleminin nasıl olduğunu aşağıdaki görselde kısaca anlayabilirsiniz. Gördüğünüz gibi orijinal vektörümüz, dönüşüm matrisi ile işleme girdikten sonra iki katına çıkmıştır. Bu doğrusal dönüşümün bir örneğidir. Ancak başka matrisler yansıma, dönme ve öteleme gibi farklı türde doğrusal dönüşümler gerçekleştirir. Doğrusal cebir bu dönüşümlerin ardındaki aritmetiği belirtir. 

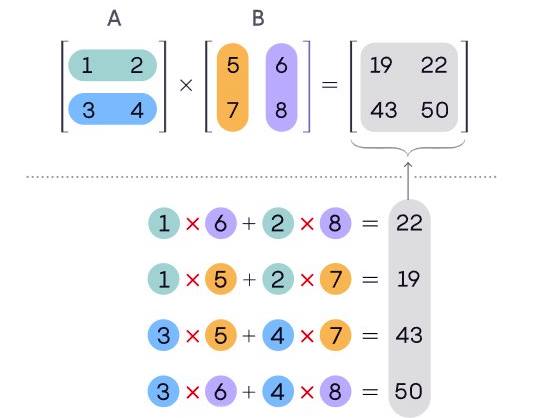
Aynı boyuttaki iki matrisin toplanması, birbirine karşılık gelen elemanların birbirine eklenmesi biçimindedir. Ancak matrislerin konuyu yeni öğrenen öğrencileri şaşırtan bir özelliği vardır. Çarpma yaptığınızda sonuç, çarpımı yaptığınız sıraya bağlıdır. Yani matematik diliyle söylersek matrislerde çarpmanın değişme özelliği yoktur.

Çünkü iki matrisin çarpılması, hem matrisin her sütununda matematiksel işlemlerin yapılması hem de sonuçların yeni bir matrise girilmesi anlamına gelir. Zaten matrisleri yararlı kılan özelliği de budur. Çarpma işleminin nasıl yapıldığına dair fikir edinmek isterseniz aşağıdaki örneğe göz atabilirsiniz.

Sonuç Olarak

Matrisler ile işlem yapmak için kuralları bilmek ve bolca pratik yapmak gerekir. Ancak bunları öğrendikten sonra uygulama yapmak kolaydır. Sonucunda bilgisayarlar devasa matrislerde saklanan verileri işlerler. Bankalar şifreleme için matrislerden faydalanır. Matris büyüdükçe şifrelemenin güvenlik düzeyi de artar. Kısaca aktarmaya çalıştığımız gibi matrisler bir çoğumuzun düşündüğünden çok daha fazla işe yarar.

Kaynaklar ve ileri okumalar:

• Explained: Matrices; http://news.mit.edu
• Matrix Multiplication Inches Closer to Mythic Goal. Yayınlanma tarihi: 23 Mart 2021. Kaynak site: Quanta magazine. Bağlantı: Matrix Multiplication Inches Closer to Mythic Goal
• The Theorem That Applies to Everything from Search Algorithms to Epidemiology. Yayınlanma tarihi: 21 Nisan 2020. Kaynak site: Scientific. Amreican. Bağlantı: The Theorem That Applies to Everything from Search Algorithms to Epidemiology

Size Bir Mesajımız Var!

Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel