Matematikçiler fazla büyük konuşmayı sevmezler. Çünkü söyledikleri sözlerin bir zaman sonra çürütülebileceğini bilirler. Örneğin yakın zamana kadar, π sayısının herhangi bir basamağını örneğin kentilyonuncu ondalık basamağının değerini bilmemiz imkansız görünüyordu. Bunu yapmak için tek yönteminin önceki basamakları birer birer hesaplamak olduğunu düşünüyorduk. Ancak ilerleyen yıllarda yanıldığımızı anladık.

1997 yılında, daha önceki rakamları hesaplamaya gerek kalmadan rastgele bir konumdan başlayarak pi sayısının istenilen basamağının hesaplanmasına izin veren bir formül bulundu. Tahmin ettiğininiz gibi bu formül bu konuda çalışma yapan üçlünün yani David Bailey, Peter Borwein ve Simon Plouffe’nin adı ile isimlendiriliyor. Bu nedenle de formül, BBP formülü ya da tam adı ile Bailey Borwein Plouffe formülü olarak bilinmektedir.
Pi Sayısı Hakkında Bilmediğimiz Çok Şey Var

Binlerce yıldır matematikçiler Pi sayısı ile ilgilendiler. Ancak uzun ve yoğun çalışmalara rağmen, bu sayı hakkında birçok basit soru cevapsız kaldı. Örneğin Pi sayısının rakamları rastgele sıklıkta ortaya çıkıyor gibi görünse de bunu kanıtlayamadık. Öyle gibi gözükse de bu sayının rastgele bir sayı olduğu da söylenemez. Çünkü biz öngöremesek de bu basamaklardaki rakamların ne oldukları belirlidir.
Pi sayısının normal bir sayı olup olmadığını bile bilemiyoruz. Rakamların her sıralanışının görülme olasılığı eşit olan ondalık sayıların normal sayı olduğu söylenir. Teknik olarak rastgele olmasalar bile, böyle sayılar rastgele gibi görünür.
Pi sayısının basamaklarındaki rakamlara bakarak ve istatistiksel sınamalar yaparak, normal olup olmadığını belirleyebilirsiniz. Yine de şimdiye dek gerçekleştirilen testlerden Pi sayısının normal olup olmadığı halen anlaşılamadı. Bildiğimiz tek bir şey var. O da basamak sayısı arttıkça her rakamın görülme sıklığının birbirine giderek yaklaşması.
Pi Sayısını Yıllar İçinde Öğrendik
Arşimet, bir dairenin içine ve çevresine çizilen çokgenleri kullanarak Pi sayısını hesaplamaya çalıştı. (Arşimet’in Pi Sayısını Hesaplamak İçin Kullandığı Güzel Ve Basit Yöntem). 1666 yılında veba salgını karantinası esnasında, Isaac Newton pi sayısının ilk 15 ondalık basamağını hesapladı. Sonra da bunu can sıkıntısından yaptığını söyledi. 1761’de İsviçreli matematikçi Johann Lambert, Pi sayısının irrasyonel olduğunu bizlere gösterdi.
Bir asırdan fazla bir süre sonra, Ferdinand von Lindemann Pi sayısının aşkın bir sayı olduğunu kanıtladı. Bu da tamsayı katsayılı hiçbir polinomun π’ye eşit bir kökü olamayacağı anlamına geliyordu. Bu aynı zamanda antik Yunan’dan beri bilinen bir sorunun cevabı oldu. Pi sayısının aşkın bir sayı olduğunun ispatı verilen bir dairenin alanıyla bir kare oluşturmanın imkansızlığını da gösterdi.
Bilgisayar çağının başlangıcından bu yana, π’nin bilinen rakamlarının sayısı katlanarak arttı. 1949’da π’nin iki binden fazla basamağı ENIAC (Elektronik Sayısal Entegratör ve Bilgisayar) kullanılarak hesaplandı. Bulunan rakam yığınının içinde John von Neumann bir desen aradı ancak ne yazık ki bulamadı.
1973’te π bir milyon basamağa, 1989’da bir milyara ve 2002’de bir trilyona ulaştı. Şu anda bu sayının 62.8 trilyon basamağını biliyoruz. Ümitsizce her geçen gün yeni basamaklar aramaya devam ediyoruz. (Binlerce Yıldır Dünyayı Büyüleyen Pi Sayısı Hakkında Bazı İlginç Bilgiler)
Bailey Borwein Plouffe Neden Farklıdır?
1997’de Bailey, Borwein ve Plouffe Pi sayısı için dikkate değer bir formül yayınladı. ( Çalışmalarını yazının sonunda inceleyebilirsiniz.) Bu formül matematik camiası için bir sürpriz oldu.
Daha önceki çalışmaların hepsi Pi sayısının açılımını hesaplamak ile ilgili idi. Ancak bu formül olaya farklı açıdan yaklaşıyordu. Pi sayısının basamaklarını hesaplamadan istenilen herhangi bir basamağını bulabiliyordu. Formülün keşfi büyük bir ustalık gerektirdi, ancak bir kez bulunduğunda kanıtı şaşırtıcı derecede basitti.
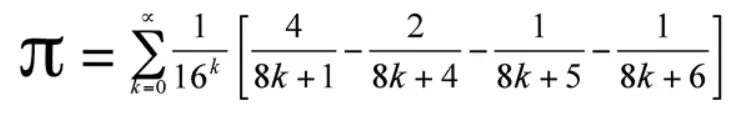
Ancak bu noktada hatırlatmakta fayda var. Yukarıda gördüğünüz korkutucu gibi gözüken formül sayesinde hesaplanan rakamlar, onaltılık sayı tabanında bulunmaktadır. Bu formülün en büyük avantajı pi sayısının herhangi bir basamağını uygun algoritmayı kullanarak çok kısa sürede bulabilmemizdir.
İşin güzel tarafı, Bailey Borwein Plouffe formülünün varyasyonları, pi gibi diğer irrasyonel sayıları da bulmak için kullanılabilir. Onaltılık taban iki, dört ve sekizlik tabanın katı olduğu için bu formülde gerekli düzenlemeler yapıldıktan sonra bu tabanlarda da pi sayısı için istenilen basamak bulunabilir.
Nitekim 2010’da Yahoo’dan Nicholas Sze, π’nin iki katrilyonuncu basamağını bu formülün ikilik sistem versiyonunu kullanarak hesapladı ve bu basamağın 0 olduğunu söyledi. Böyle bir sonuç, Bailey Borwein Plouffe formülü olmasaydı mümkün olamazdı. Bunun gibi başka formüller var mı? Bilmiyoruz. Ancak kesin bildiğimiz şey hayır yok diyemeyeceğimiz.
Kaynaklar ve ileri Okumalar
- Bailey, David, Peter Borwein and Simon Plouffe (1997), ‘On the rapid computation of various polylogarithmic constants’, Mathematics of Computation, 66, 903–13.; Bağlantı: https://www.ams.org/
- David H. Bailey; The BBP Algorithm for Pi; Bağlantı: https://www.davidhbailey.com
- Bailey–Borwein–Plouffe formula; Bağlantı: https://en.wikipedia.org/
- Pi record smashed as team finds two-quadrillionth digit; yayınlanma tarihi: 16 Temmuz 2010; Bağlantı: https://www.bbc.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel