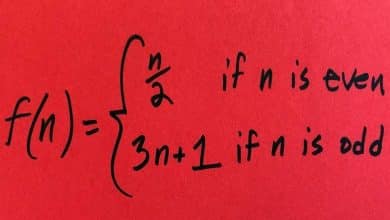Bildiğiniz gibi bir kümenin öğelerinden bazılarını içeren yeni bir küme oluşturduğunuzda, bu yeni küme asıl kümenin alt kümesi olarak adlandırılır. Kümeler ünitesinin başında yer alan alt küme soruları ise öğrencilerin en çok zorlandıkları soru tiplerinden bazılarını barındırır.

Lise sınıflarında alt kümelerle ilgili soruları öğrenciler genellikle sayma (permütasyon ve kombinasyon) bilgileriyle çözerler. Benim bu yazıda göstereceğim yöntem ise kümelerde doğruluk tablosu yapmaya dayanıyor. Bildiğim kadarıyla bu yazı, söz konusu yöntemden bahseden ilk yazı olacak… Şimdi bu farklı yöntemi bir örnek üzerinde açıklayalım.
Soru: A = {a, b, c, d} kümesinin alt kümelerinden kaç tanesinde a ve b elemanı bulunur, c elemanı bulunmaz?
Çözüm: Anlatacağım yöntemde soruyu önermeler mantığı ile çözeceğiz. Kümenin elemanlarını sanki birer mantıksal önermeymiş gibi düşünüp doğruluk tablosunu yapacağız. (Aşağıdaki şekli inceleyiniz.)

Yukarıdaki tablodaki her satır, bir alt kümeyi gösteriyor. 1 sayısı elemanın alt kümeye alındığı, 0 ise alınmadığı şeklinde yorumlanmalıdır. Örneğin birinci satırda tüm elemanlar alınıyor (kümenin kendisi), ikinci satırda d hariç tüm elemanlar alınıyor, üçüncü satırda c hariç tüm elemanlar alınıyor vs. Böylece dört elemanlı A kümesinin tüm alt kümelerini eksiksiz olarak listelemiş oluyoruz.
Tablonun, tüm alt kümeleri verdiğini görünüz. Artık soruyu çözmeye hazırız. Bize A’nın kaç alt kümesinde a ve b’nin bulunup c’nin bulunmadığı soruluyor. Yani tablodaki a ve b sütunlarının 1; c sütununun ise 0 olduğu satırların sayısı istenmektedir. (Aşağıdaki şekilde sarı renkli hücreler.)

Bu şartlara uyan sadece iki satır vardır. Çünkü a, b ve c sütunlarını sadece bir farklı şekilde doldurabiliriz (a=1, b=1 ve c=0) ama d için iki itimal var d=0 ya da d=1 olabilir. Bir kez tablonun mantığını kavradığımızda artık soruyu zihinden de çözebiliriz. Şimdi bu bilgilerimizi aşağıdaki soruyu çözmek için kullanalım.
Alt Küme İle İlgili Sorular
Soru: A={a, b, c, d} kümesinin alt kümelerinden kaçında b bulunur?
Çözüm: Bize tablodaki sütunların kaç tanesinde b’nin değerinin 1 olduğu sorulmaktadır. (4 elemanlı bir kümenin 16 alt kümesi olduğunu hatırlayalım.) Doğruluk tablosunda her sütunda 1 ve 0’ların sayısı eşit olduğuna göre 8 tane “1” ve 8 tane de “0” olmalıdır. O halde cevap 8’dir. Şimdi biraz daha zor bir soru çözelim.
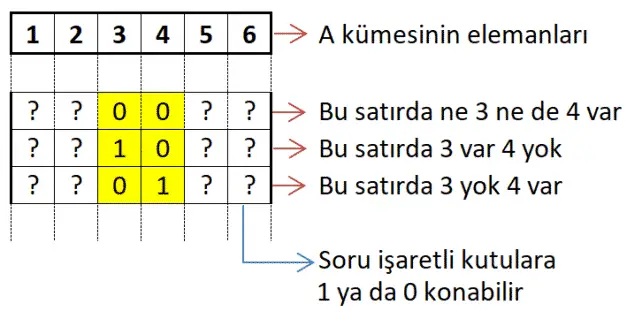
Soru: A = {1, 2, 3, 4, 5, 6} kümesinin, içinde 3 veya 4 elemanlarından en çok birinin bulunacağı alt kümelerinin sayısı kaçtır?
Çözüm: A kümesinin tablosunu yapmak pratik olmaz çünkü 26 = 64 satır içeriyor. Ancak zaten tablo yapmamıza da gerek yok, önemli olan tablo mantığını kavramış olmak. Şimdi, bizden istenen 3 veya 4 elemanlarından en çok birinin bulunduğu alt kümelerin sayısı. Yani bize aşağıdaki tablodaki sarıya boyanmış satırlardan kaç tane olduğu soruluyor. Dikkat edilirse her satırda 4 tane “?” işareti var. Soru işaretlerinin yerini kaç farklı şekilde doldurabiliriz? Tabi ki cevap 24=16’dır. Ve bu şekilde üç farklı satır olduğuna göre cevap 3×16=48 olur. Bu yöntemle bir kez tablo mantığı anlaşıldıktan sonra her soru kolayca çözülebilir. (Aşağıdaki şekli inceleyiniz.)
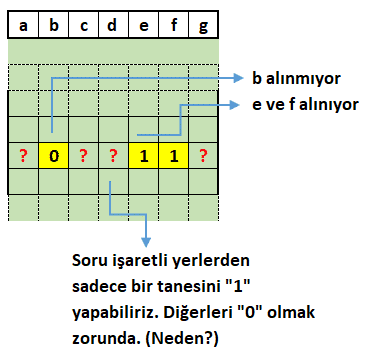
Soru: A = {a, b, c, d, e , f, g} kümesinin üç elemanlı alt kümelerinin kaçında e ve f bulunur, b bulunmaz?
Çözüm: Aşağıdaki şekilde sarı ile boyalı hücrelere dikkat ediniz. Soru işaretli yerlerin sadece bir tanesine 1 koyabiliriz, diğerleri sıfır olmak zorunda. (Üç elemanlı alt küme sayısı sorulduğu için.) b, e, f dışında doldurabileceğimiz sadece 4 pozisyon var. O halde yanıt 4’tür. (Şekli inceleyiniz.)
Bu yazıda sizlere soru çözerken kalıpların dışına çıkmanın bir yolunu göstermek istedim. Bu yöntemi kavradıktan sonra başka soru tiplerini nasıl çözebileceğinizi kendi kendinize keşfedeceğinize inanıyorum.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel