Pi Sayısından Daha İlginç Sayılar İle Tanışın

Matematik dünyasının en ilginç sayısı elbette Pi sayısıdır. Bu sayı o kadar meşhurdur ki kendine has bir kutlama günü bile vardır. Aslında Pi sayısı 3 ile 4 arasında çok da ilginç bir sayı değildir. Ancak onu asıl önemli kılan şey, çember ile ilgili olsun ya da olmasın pek çok yerde karşımıza çıkmasıdır. Pi Günü’nü kutlamanın asıl nedeni, tamamen soyut bir konu olan matematiğin evrenimizi bu kadar iyi tanımladığının ortaya çıkmasıdır. Ancak kutlamayı hak eden başka ilginç sayılar da vardır. Bu yazıda bazılarını sizlere hatırlatalım.

1- Tau sayısı

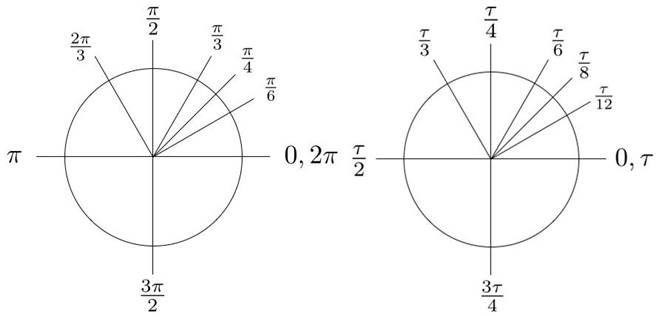
Pi’den daha ilginç bir sayı var ise o da iki Pi’dir. Diğer bir deyişle Pi sayısının iki katıdır. Hatta bazı matematikçiler pi sayısının başka bir matematik sabiti olan bu sayı ile değiştirilmesi gerektiğini öne sürüyor. Bu yeni sabit (τ) ile sembolize edilen Tau sayısıdır. Tau sayısı yaklaşık olarak 6,28 değerine sahiptir. Pi bir çemberin çevresini çapıyla ilişkilendirir. Oysa tau sayısı bir çemberin çevresini yarıçapıyla ilişkilendirir.

Pi sayısı bildiğiniz gibi yarım çemberin radyan cinsinden açı ölçüsüdür. Ancak hesaplamada bazı kolaylıklar sağladığı için Tau sayısı, tam çemberin radyan cinsinden açı ölçüsü olarak daha kullanışlıdır. Ancak Pi sayısı, matematiğe o kadar yerleşti ki, çıkarmak son derece zor. Tau’yu Pi’nin yerine kullanmak yerine ikisini beraber öğretmek daha pratik bir yaklaşım olur.

2- Doğal Logaritma: e

Matematikte bir başka ilginç sayı da hiç kuşkusuz 18. yüzyıl matematikçisi Leonhard Euler’in anısına “e” olarak tanımladığımız bir sayıdır. Sonsuza uzanan değeri ondalık basamakların ilk altısıyla 2,718281 olarak kabul edilen bu sayı, kendisini tanıtan matematikçinin ismiyle “Euler sayısı” olarak da bilinmektedir.

Euler sayısı irrasyonel bir sayıdır, yani onu basit bir kesre indiremezsiniz. Tıpkı pi gibi, e sayısının da ondalık basamakları tekrar etmeden sonsuza kadar gider. Nüfus artışını belirlemede, finansal matematikle uğraştığımız zamanlarda, olasılık ve istatistik hesaplamalarında e sayısı sıkça karşımıza çıkar.

Aslında yaşamda değişim ya da büyümeyi içeren bir şey yapmak istediğimizde muhtemelen arka planda bir yerlerde bu sayı gizlidir. Ama tüm bu büyüme ilişkilerinin içinde ilgimizi en çok çeken şey ise elbette paradır. Çünkü e sayısı, bileşik faiz hesaplarında karşımıza çıkmaktadır. ( Detaylar için: Bileşik Faiz İle Euler Sayısının İlişkisi Nedir?)

3- Hayali Bir Sayı: i

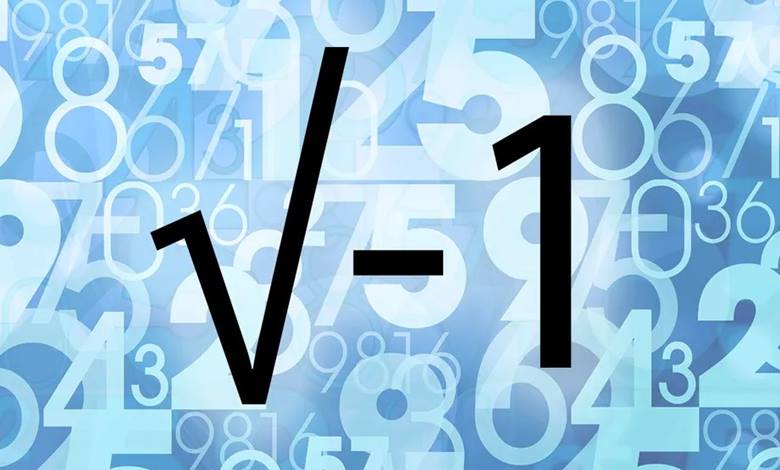
Karmaşık sayılar ve sanal sayıları öğrenen öğrencilerin aklına çoğu zaman bu benim ne işime yarayacak sorusu gelir. Aslında bir yerde de haklıdırlar. Sonucunda gündelik hayatımızda i sayısı ile fazla karşılaşmayız.

20. yüzyılın başlarında fizikteki iki devrim— Einstein’ın göreliliği (önce özel, sonra genel) ve kuantum mekaniği— gerçek sayıların ötesinde bir matematik ihtiyacı olduğunu ortaya koydu. O zamandan beri, hem gerçek hem de sanal parçalardan oluşan karmaşık matematik, Evren anlayışımızla ayrılmaz bir şekilde iç içe geçmiş durumda. 

Bugün okullarımızda doğal sayılardan başlayarak, tamsayılar, rasyonel sayılar biçiminde birbirini kapsayan sayı ailelerini öğretiyoruz. En sonunda da karmaşık sayılara geliyoruz. Çünkü “Hangi sayının karesi -1 yapar?” sorusunu sorduğumuz zaman bir noktadan sonra cevap alamıyoruz. Bu sorunun cevabının -1’in karekökü diğer deyişle x=√ -1 biçiminde olur ve bunun reel sayılarda bir karşılığı yoktur. Bu durumda da yeni bir sayı sistemine daha ihtiyaç duyulur.

Sanal (imaginary) sayılar adı, filozof ve matematikçi Rene Descartes tarafından 1637 yılında verildi. Devamında da Euler bu sayılara bir kimlik kazandırdı. Bu sayede de √-1 , “i” olarak gösterilmeye başlandı. Sanal sayılar işin içine karıştığı zaman karşımıza yeni bir sayı sistemi çıkar. Bu sistemin adı karmaşık sayı sistemidir.

i Üzeri i

i sayısını ilginç buluyorsanız bir de i üzeri i sayısını düşünün. Baştan söyleyelim, şaşırabilirsiniz. Lisede karmaşık sayılar konusunu görenler i sayısının kuvvetlerini hesaplamasını bilir. Bu sayının kuvvetlerini aldığınız zaman aşağıda gördüğünüz gibi sonuçlar elde edersiniz.

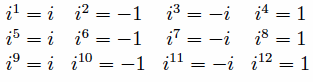
Peki, i sayısı üzeri i sayısının sonucu kaç çıkacaktır. Bu sayının sonucu tam olarak söylemek gerekirse 0.2078795763507619085… biçiminde uzayıp giden bir irrasyonel sayıdır. Bu sonucun nasıl ortaya çıktığını anlamak için göz atabilirsiniz. ( Sanal Sayılar ( i Sayısı) Hakkında Bilmeniz Gereken 3 İlginç Şey)

5- Apéry Sabiti

Matematikçilerin en ilginç bulduğu sayılardan biridir Apery sabiti yani zeta(3). 1979’da Fransız matematikçi Roger Apery, 1,2020569 ile başlayan ve sonsuza dek devam eden bir sayının irrasyonel olduğunu kanıtlayarak ona Apery sabiti dedi ve ayrıca zeta(3) olarak yazılır. Burada zeta(3), 3 sayısını yerleştirdiğinizde Riemann zeta fonksiyonudur.

Peki bu sabiti bu denli ilginç kılan nedir? Apery sabiti, elektronun manyetizmasını ve açısal momentuma olan yönelimini gösteren denklemler gibi fizikteki büyüleyici noktalarda ortaya çıkıyor. Bunun nedeni de henüz net olarak bilinmiyor.

6- Belphegor Asalı: 1000000000000066600000000000001

Yukarıdaki sayıya dikkatli bakacak olursanız bazı ilginçlikler fark edeceksiniz. Sayıda rakamlarının dizilişi soldan sağa ve sağdan sola aynıdır yani palindromik bir asal sayıdır. Ayrıca tam ortasında 666, bunun iki yanında da 13’er adet 0 bulunmaktadır. Bu şeytani sayı 1 0(13) 666 0(13) 1 olarak kısaltılır. Buradaki (13), 1 ile 666 arasındaki sıfırların sayısını gösteriyor.

Batı kültürlerinde 666 ve 13 sayılarına atfedilen uğursuzluktan dolayı bu sayıya cehennemin yedi prensinden biri olan Belphegor’un adı verilmiş. Sayının, pi’nin baş aşağı hali gibi görünen kendi şeytani sembolü bile var. Sembol, gizemli Voynich el yazmasındaki bir gliften türetildi.

7- Altın Oran:  Phi Sayısı

Matematiği sevin ya da sevmeyin altın oran ismini mutlaka bir yerlerde duymuş olmalısınız. Bu sayı matematiğin pi sayısından sonra en ünlü sayısıdır desek hata yapmış olmayız. Altın oran, Bir başka irrasyonel sayı olan Yunanca phi (φ) harfi ile gösterilmektedir. Değeri ise φ = (1 + √5) / 2 = 1.6180339887498…biçimindedir.

Ne yazık ki altın oran ile ilgili duyduğumuz olağanüstü bilgilerin çoğu abartılıdır. Ancak bu altın oranın kendi başına ilginç bir sayı olmadığı anlamına gelmemelidir. Altın oran, ünlü Fibonacci dizisiyle yakından ilişkilidir. Fibonacci dizisi, hem popülasyonların büyümesiyle hem de şekillerin birbirine uydurulabilmesiyle bağlantılı olduğu için kesinlikle doğada ortaya çıkar. 

Örneğin, çam kozalaklarının dip kısmındaki spirallerin sağa dönük olanlarının sayısı genelde 8, sola dönük olanların sayısı ise genelde 13’tür. Bir çok çiçek cinslerinin (özellikle de papatyaların) taç yapraklarının sayısı da genellikle Fibonacci Dizisi’nin bir elemanı olmaktadır. Ancak bunun da mistik değil, bilimsel bir açıklaması vardır. Detaylar burada: Altın Oran Nedir? Hakkında Duyduklarımıza İnanmalı mıyız?

Kaynaklar ve ileri okumalar:

• 12 numbers that are cooler than pi; Yayınlanma tarihi: 14 Mart 2023. Kaynak site: Live Science. Bağlantı 12 numbers that are cooler than pi/
• Pi gets all the fanfare, but other numbers also deserve their own math holidays. Yayınlanma tarihi: 8 Mart 2023. Kaynak site: Conversation. Bağlantı: Pi gets all the fanfare, but other numbers also deserve their own math holidays

Size Bir Mesajımız Var!

Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel