Bir “an” ne kadar kısadır? Bir saniye mi? Saniyenin onda biri mi? Bir mikrosaniye mi? Peki ya 100 yıl? Bu kesinlikle bir an gibi görünmüyor. Ancak dev bir sekoya ağacı için 100 yıl çok da önemli bir zaman değildir. Peki bir anı matematiksel olarak nasıl tanımlayabiliriz? Bu sorunun cevabı bizi sonsuz küçükler (infinitesimal) tanımına götürecektir.

İki sayı aldığımız zaman bu iki sayının arasında her zaman bir başka sayının var olacağını biliriz. Bu mantıkla 0 ile 1 sayısının arasına istediğimiz kadar reel sayı sığdırabiliriz. Bu sayılardan biri 0.00000000000000001 olsun. Bu sayı çok küçük gibi görünse de, daha küçük bir sayı elde etmek için yapmamız gereken tek şey 10’a bölmektir. Yani bir şey ne kadar küçük gözükürse gözüksün daha küçüğünü elde etmek her zaman olasıdır.
Newton ve Leibniz kalkülüsü geliştirdikleri zaman sonsuz küçüklükle yüzleşmek zorunda kaldılar. Çünkü bir nesnenin “anlık hızı” ile ilgili hesaplamayı yapmak zorunda kalmışlardı. Anlık hız bir şeyin zaman içinde belirli bir anda hareket ettiği hızdır (arabanızın hız göstergesindeki sayı gibi). Bu hızı hesaplamak için de aşağıdaki yaklaşım benimsenecekti.

Belirli bir zaman aralığında ortalama hızın nasıl hesaplanacağını biliyoruz. Bunun için kat edilen toplam mesafeyi bulmak ve toplam süreye bölmek yeterlidir. Örneğin cisim 1 saniyede 1 metre yol alıyorsa ortalama hızı 1 m/s’dir. Peki ya daha iyi bir ölçüm cihazınız varsa? Bu cihazla nesnenin saniyenin ilk 10’da birinde 20 cm yol kat ettiğini hesapladığımızı varsayalım. Şu anki anlık ortalama hız 2 m/s’dir ve bu ilkine göre daha iyi bir yaklaşımdır.
Ancak bu yine de sadece bir yaklaşımdır. Gerçek değeri elde etmek için giderek daha küçük zaman aralıkları almanız ve doğruluğu giderek artan ölçüm ekipmanlarına sahip olmanız gerekir. 17. yüzyılda matematikçilerin bunu aşma yöntemi sonsuz küçüklerden bahsetmekti.
Sonsuz Küçükler Hesabı Nasıl Yapılır?
Kalkülüs son 400 yıldaki en önemli matematiksel keşif olarak kabul edilmektedir. Fizik ve mühendislikteki pek çok gelişme kalkülüs ile bir biçimde ilişkilidir. Bu, dikkatli bir gözlem ve sonsuz küçükler hesabı sayesinde mümkün olabilmiştir. Bunun nasıl olduğunu anlamak için bir örneğe bakalım.
Bu örnekte bir dairenin alanını, içine çizilen üçgenlerin alanı yardımı ile toplamaya çalışalım. İlk dairemizi dört üçgene böldük. Ancak görselde de görebileceğiniz gibi dairenin içinde önemli bir miktar boşluk kaldı. Bu nedenle bu üçgenlerin alanlarının toplamı dairenin alanına eşittir diyemez. Bu hatayı azaltmak için daha fazla üçgen oluşturmaya çalışabiliriz. Evet, bu biçimde hata azalır ancak sonucumuz yine de hatalıdır.
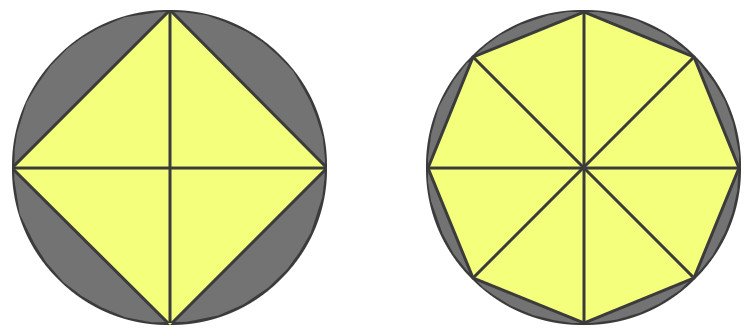
Bu hatayı tamamen ortadan kaldırmak için onu sonsuz sayıda üçgene bölmemiz gerekir. işte bu noktada sonsuz sayıda üçgenin, sonsuz sayıda tabanı hemen hemen dairenin çevresini kaplayacaktır. Bu tabanlarımız artık o kadar küçüktür ki aradaki eğrilik neredeyse yok olmuştur. İşte bu sonsuz küçükler fikrine güzel bir örnektir.
Şimdi devam edelim. Aşağıda soldaki şekli biraz bozalım. Sonuçta elimizde aynı alana sahip sonsuz sayıda üçgenimiz var. Bu üçgenleri kesip, tek bir noktada birleştirdiğimizi düşünelim. Gördüğünüz gibi yeni üçgenimizin tabanı aslında çemberin çevresine neredeyse eşittir. Bu sayede de bir dairenin alanını neredeyse bulmak mümkün olacaktır. Teoride bu cevap doğrudur ancak pratikte yine hatalıdır.
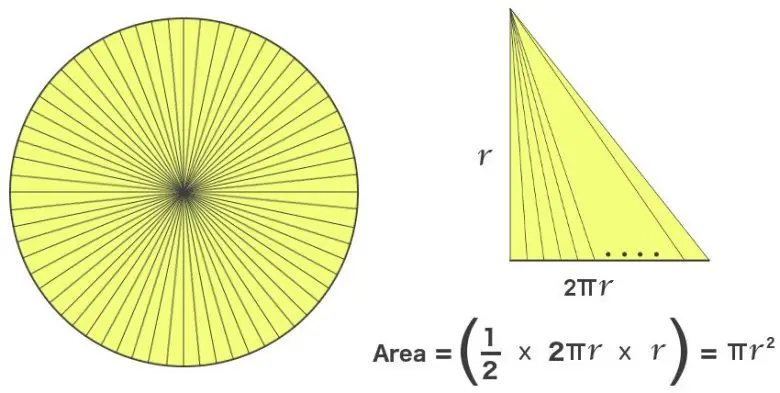
Bu hesaplamanın doğru olması için tabanın sonsuz küçük olması gerekir. Ancak ne kadar ince üçgen çizersek çizelim aslında daha da küçüğünün çizilebileceğini biliyoruz. Bu sonuç bir matematikçiyi rahatsız etse de, yani yukardaki neredeyse cümlesinden çok hoşlanmasak da, çoğunluk bunu görmezden gelir. Çünkü gördüğümüz gibi, elde edilen sonuçlar yanlış değildir. İşte bu nedenle sonsuz küçükler hesabı uzun bir süre matematikçileri ikiye ayırmıştır.
Sonsuz Küçükler Fikri Kolay Kabul Edilmeyecekti
Sonsuz küçükler ile ilgili hesaplamalar matematikte önemli bir kırılma anıydı. Ancak zamanın bazı bilim insanları ve çeşitli kurumlar bu fikri saçma bularak reddettiler. Eleştiriler, sonsuz küçüklerin matematiğin temelini çürüttüğü ve kaçınılmaz olarak ciddi hatalara neden olacağı şeklinde suçlamalar içeriyordu. Bir şeyin sonsuza kadar bölünebileceği fikri, Platon’un bölünemezler idealine de ters düşüyordu.
Gökbilimci Johannes Kepler’i genellikle gezegenler ile ilgili çalışmaları ile tanırız. Ancak aslında kendisinin matematiğe de büyük katkıları bulunmuştur. Bunlardan bir tanesi de 1615’te, variller gibi kavisli şekillere sahip katıların hacimlerini hesaplamanın bir yolunu bulmasıydı.

Kepler, bir fıçının veya herhangi bir 3 boyutlu şeklin hacmini bulmak için onu ince katmanlardan oluşan bir yığın olarak hayal etti. Toplam hacmi bulmak için yapmamız gereken şey, tüm katmanların hacimlerini toplamaktı. Kepler’in çözümü, sonsuz küçükler kavramını kabul ettiği için doğruydu. 1615’te sonuçlarını Nova stereometria doliorum vinariorum’da (Şarap fıçılarının yeni katı geometrisi) adlı kitabında yayınladı. Kepler bu çalışması ile 17. yüzyılda Isaac Newton ve Gottfried Leibniz tarafından kalkülüsün geliştirilmesinin yolunu açtı.
Sonsuz Küçükler Ve İntegral Hesabı
Sonsuz küçükler metodunun öncüleri bilimsel çevrelerin bu fikri kabul etmemesini fazla da umursamadılar. Sonunda 19. Yüzyılın başında Fransız matematikçi Augustin-Louis Cauchy sayesinde de sonsuz küçükler fikri matematikte hak ettiği konuma oturdu. Sonsuz küçükler sonsuz derecede küçük olanlarla başa çıkmamıza yardımcı olur. Ancak bunun işlemlere nasıl dahil edileceği Cauchy’nin limit kavramını tanımlaması ile olası olmuştur.
“Günlük yaşamda limit ne işime yarayacak?” diye sorarsanız; buna cevap vermek pek kolay değil. Hatta doğrudan hiçbir işine yaramayacak desek çok da yanılmış olmayız. Tabi büyük resme odaklanırsak bazı şeyler değişecektir.
Asla değişmeyecek bir şey, dünyanın sürekli değiştiği gerçeğidir. Türev ve integral değişimin matematiğidir. Dolayısıyla değişimin olduğu her yerde bu iki kavram kendisini gösterecektir. Bunların olduğu her yerde de aslında limit karşımıza çıkacaktır.
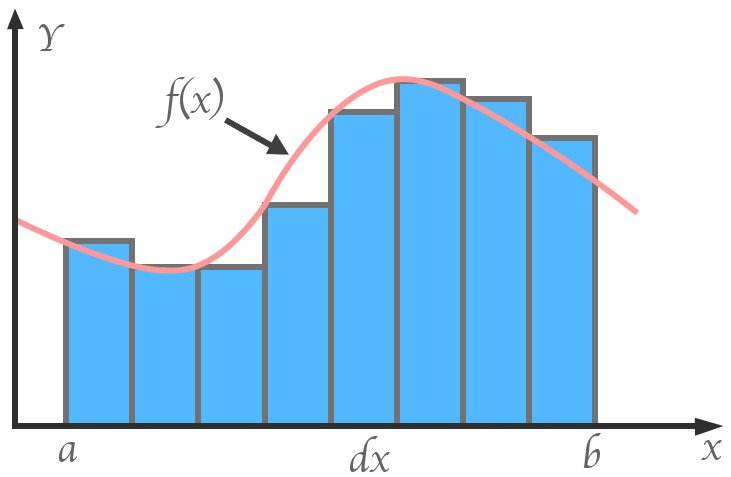
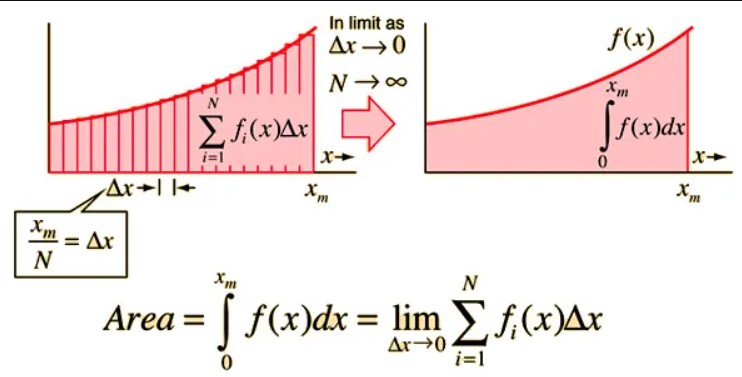
Bir fonksiyonun integralini hesaplamaya kalktığımız zaman, esasen fonksiyona karşılık gelen eğrinin altındaki alanı hesaplarız. Ancak, yukarıda bir dairenin alanını hesaplama örneğinde anlattığımız gibi, bunu eğriyi sonsuz derecede küçük tabana sahip dikdörtgenlere bölerek yaparız. Dikdörtgenler ne kadar ince olursa, hata payı da o kadar küçük olur. Yukarıda ‘dx’ dediğimiz şey aslında sonsuz küçük bir birimdir.
Kaynaklar ve İleri Okumalar:
- Kepler: The Volume of a Wine Barrel; Bağlantı: https://www.maa.org/
- The Opposite of Infinity – Numberphile; Kaynak site: Youtube. Bağlantı: The Opposite of Infinity – Numberphile/
- What Is The Opposite Of Infinity?; Yyaınlanma tarihi: 19 Ekim 2023. Kaynak site: Science ABC. Bağlantı: What Is The Opposite Of Infinity?/
Matematiksel



