Matematikte çözülemeyen en eski problem yaklaşık iki bin yıllıktır ve size tek mükemmel sayı olup olmadığını sorar.

Mükemmel sayılar hem matematikçileri hem de matematikçi olmayanları tarih boyunca büyülemiştir. Bunun en temel nedeni tanımlanmalarının ve anlaşılmaların kolay olmasından gelir. Ayrıca günümüzde asal sayılar üretmek için bir formül bulma çalışmasında mükemmel sayılar önemli rol oynar. Tek mükemmel sayılar sorununu anlamak için öncelikle mükemmel sayıların ne olduğunu hatırlamalısınız.
Mükemmel Sayı Nedir?
Her pozitif tamsayı çarpanlarına ayrılabilir. Bir sayıyı çarpanlarına ayırmak, onu iki tam sayının çarpımı olarak yazmak anlamına gelir. Her sayının çarpanlarından ikisi kendisi ve 1 sayısı olacaktır. Bir sayının kendisi ve 1 sayısından başka çarpanı ( ya da böleni) yoksa da o sayı bir asal sayı olarak kabul edilecektir.
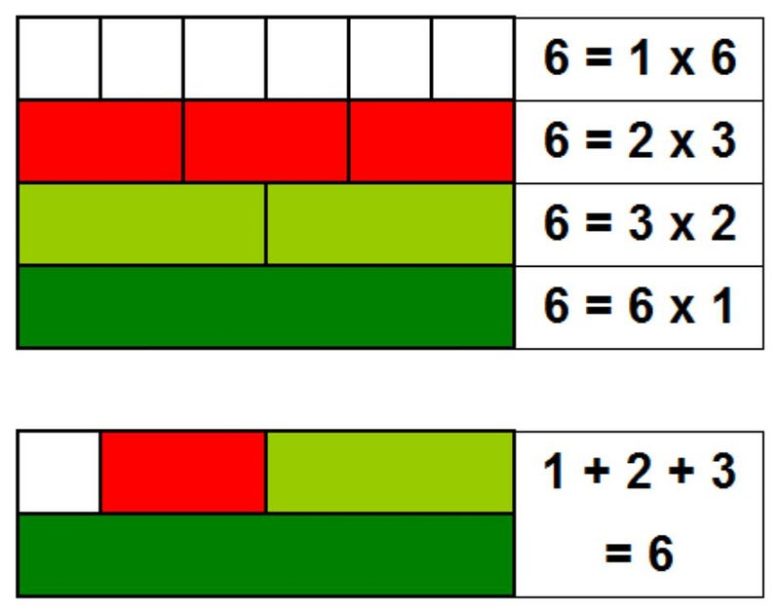
Bir sayının mükemmel olabilmesi için (kendisi hariç) pozitif tam bölenlerinin toplamı bu sayıya eşit olmalıdır. Bunun ne anlama geldiğini 6 sayısı için yukarıda görebilirsiniz. En küçük mükemmel sayı 6’dır. Çünkü bu sayı 6, 2, 3 ve 1’e tam bölünmektedir. Ayrıca 1+2+3=6 toplamına da eşittir. İkinci sırada gelen ise 28 sayısıdır. Bu sayı da 1, 2, 4, 7 ve 14’e bölünür ve 1+2+4+7+14=28’e eşittir.
Mükemmel sayıları tanımlamak kolaydır ancak örneklerini bulmak farklı bir konudur. Öklid mükemmel sayıların temellerini 2000 yıl önce attı ve ilk dört mükemmel sayının 6, 28, 496 ve 8128 olduğunu biliyordu.
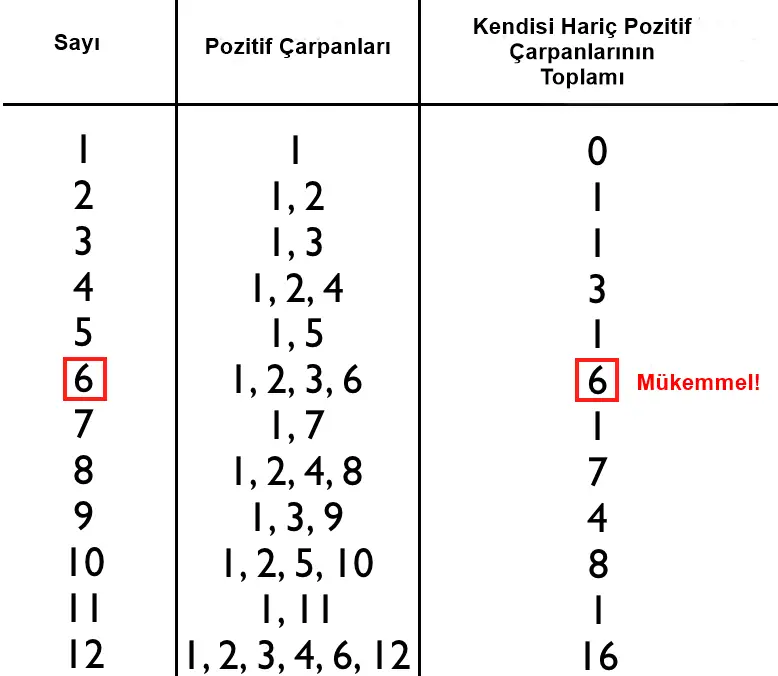
Bugüne kadar 51 mükemmel sayı keşfedildi. Aşağıda mükemmel sayıların bazılarının bir listesini görebilirsiniz. Ancak sizin de dikkatinizi çekeceği gibi bu listedeki tüm sayılar çifttir. İşte bu nedenle de matematikçiler tek mükemmel sayı olup olmadığını yıllardır sorguluyor.
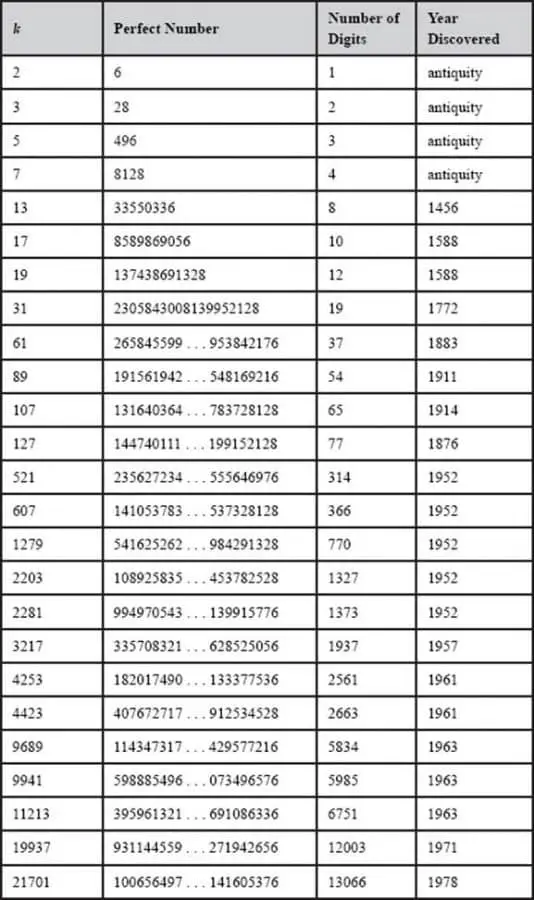
Mükemmel Sayılar Nasıl Hesaplanır?
- 6’yı çarpanlara ayırmanın iki yolu vardır. ( 6=1×6 ve 6=2×3) ve listenin ilk iki sayısı 1 ve 2’dir.
- 28’i çarpanlara ayırmanın üç yolu vardır. ( 28=1×28, 28=2×14 ve 28=4×7) ve listenin ilk üç sayısı 1 ve 2 ve 4’tür.
- 496’yı çarpanlara ayırmanın beş yolu vardır. Listenin ilk beş sayısı 1, 2, 4, 8 ve 16 biçimindedir.
- 8128 sayısını çarpanlara ayırmanın yedi yolu vardır. Listenin ilk yedi sayısı 1, 2, 4, 8, 16, 32 ve 64 biçimindedir.
Gördüğünüz gibi ilk dört mükemmel sayı belli bir düzeni takip ediyor. Örneğin, 496’yı çarpanlarına ayırmanın beş yolu 1, 2, 4, 8 ve 16’yı yani 2⁰, 2¹, 2², 2³ ve 2⁴’ü içeriyor.
Dördüncü mükemmel sayı olan 8128’i, 8128 × 1 = 8128, 4064 × 2 = 8128, 2032 × 4 = 8128, 1016 × 8 = 8128; 508 × 16 = 8128, 254 × 32 = 8128, ve 127 × 64 = 8128 biçiminde gösterebiliyoruz. Bu çarpanların hepsini ( kendisi hariç) topladığınız zaman da 8128 sonucunu elde ediyoruz. Bu durumda aşağıdaki gibi bir ilişki tanımlamamız mümkündür.

- 6 = 2 × 3 = 2¹ × (2²–1),
- 28 = 4 × 7 = 2² × (2³–1),
- 496 = 16 × 31 = 2⁴ × (2⁵–1),
- 8128 = 64 × 127 = 2⁶ × (2⁷–1).
Yukarıda mükemmel sayılar için güzel bir ilişki bulduk gibi gözüküyor. Bu durumda mesela 2¹⁰ × (2¹¹–1)’in mükemmel bir sayı olmasını beklersiniz. Ancak bunu hesapladığınızda, 1024 × 2047= 2096128 sonucunu elde edersiniz. Kontrol ederseniz, bu mükemmel bir sayı değildir.
Tek Mükemmel Sayı Arayışı Nasıl Devam Etti?
MÖ 4. yüzyılda Öklid, 2p − 1 asal ise 2p − 1(2p − 1) çarpımının mükemmel bir sayı olduğunu ileri sürmüştü. Örneğin, p=2 ise, formül size 21 × (22 – 1)= 6; p=3 ise 22 × (23 – 1)=28 sonuçlarını verecektir. Öklid mükemmel sayıları bile üretmenin bir yolunu bulmuştu ama bunun tek yol olduğunu kanıtlamadı.
400 yıl sonra Yunan filozof Nicomchaus Introdutio Arithmetica isimli, kitabını yayınladı. Bu kitabında mükemmel sayılar ile ilgili doğru olduğuna inandığı ( ama ispatlamadığı) beş varsayım ileri sürdü.
- n’inci mükemmel sayının n rakamı vardır.
- Tüm mükemmel sayılar çifttir.
- Tüm mükemmel sayılar dönüşümlü olarak 6 ve 8 ile biter.
- Öklid algoritması her çift mükemmel sayıyı üretir.
- Sonsuz sayıda mükemmel sayı vardır.
Gelecek bin yıl boyunca hiç kimse bu varsayımlardan herhangi birini kanıtlayamadı veya çürütemedi. Sonucunda bunlar gerçek olarak kabul edildi. Ancak 13. yüzyılda Mısırlı matematikçi İbn Fallus 10 mükemmel sayının yer aldığı bir liste yayınladı. Beşinci mükemmel sayı sekiz basamak uzunluğundaydı ve bu da Nikomakhos’un ilk varsayımını çürütüyordu. Bu listedeki hem beşinci altıncı mükemmel sayı 6 ile bitiyordu. Bu da üçüncü varsayımı çürütüyordu.
Ancak diğer üçü doğru kabul edildi ve problem Rönesans Avrupa’sına ulaştı. 18. yüzyılda konu ile ilgili çalışmalar yapanlara arasında Mersenne, Pierre de Fermat ve Rene Descartes gibi isimler de vardı. Descartes bir mektubunda ” … hangi yöntemi kullanırsanız kullanın, uzun zaman alır.” diye yazacaktı ve gerçekten de haklıydı.
Tek Mükemmel Sayılar Gerçekten Var mı?
Yaklaşık yüz yıl sonra St. Petersburg Akademisi’nde, Prusyalı matematikçi Christian Goldbach, 20 yaşında bir matematik dahisiyle tanıştı. İkisi posta yoluyla iletişim halinde kaldılar ve 1729’da Goldbach bu genç adamı Pierre de Fermat’ın çalışmaları ile tanıştırdı.
Bu genç adam sayılar teorisi konusunda tutkulu oldu ve sonraki 40 yılını bu alandaki farklı problemler üzerinde çalışarak geçirdi. Çalıştığı problemler arasında mükemmel sayılar da vardı ve bu genç adamın adı da Leonhard Euler’di.

Euler problemle ilgili üç atılım gerçekleştirdi. İlk olarak 1732’de sekizinci mükemmel sayıyı keşfetti. Diğer iki buluşu da sigma fonksiyonunu ile ilişkiliydi. Aşağıda tanımını gördüğünüz bu fonksiyonun yaptığı şey aslında çok basitti. İşlevi bir sayının kendisi dahil tüm bölenlerini toplamaktı.
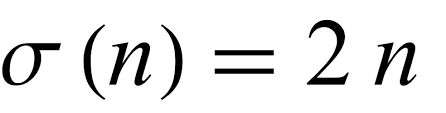
Ancak bu fonksiyon ile her zaman sayının iki katı hesaplanacaktır çünkü sayının kendisi de toplanmaktadır. Euler bu fonksiyon ile her çift mükemmel sayının Öklid formuna sahip olduğunu kanıtladı. Bu durumda Nikomakhos’un dördüncü varsayımını da kanıtlamış oldu.
Ancak Euler’in işi henüz bitmemişti. Ayrıca tek mükemmel sayılar problemini de çözmek istiyordu. Bunun için Descartes’ın her tek mükemmel sayının belirli bir forma sahip olması gerektiği yönündeki ifadesini kullanacaktı. Euler tek bir mükemmel sayının aşağıdaki koşulu karşılaması gerektiğini gösterdi, ancak Euler bile bunu kanıtlayamadı.

Sonraki 150 yıl boyunca çok az ilerleme kaydedildi ve yeni mükemmel sayılar keşfedilmedi. Matematikçiler bu bulunması zor mükemmel sayıların peşine düşmeye devam etti ve çoğu, Mersenne’in önerdiği asal sayılar listesiyle işe başladı. Ancak büyük Mersenne sayılarının gerçekten asal olup olmadığını kontrol etmek kolay iş değildi.
Mersenne Asallarının Mükemmel Sayılar İle İlişkisi Nedir?

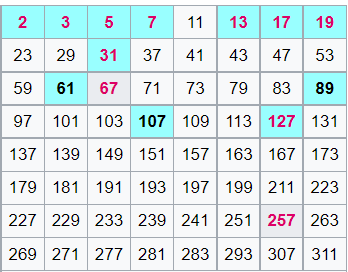
Fransız bilge Marin Mersenne mükemmel sayıları kapsamlı bir şekilde incelemişti. 1644 tarihli Cogitata Physica-Mathematica adlı kitabında asal sayılara karşılık geldiğini iddia ettiği P’nin 11 değerinden oluşan (p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 ve 257) bir liste de yayınlamıştı.
Bu nedenle günümüzde p doğal sayısı için 2p – 1 şeklindeki sayılara Mersenne sayıları, bunların asal olanlarına da Mersenne asalları deniyor. Bu listedeki ilk 7 sayı ise mükemmel sayıya karşılık geliyor. Mersenne gerçekten mükemmel bir iş çıkarmıştı. Matematikçiler mükemmel sayıları ararken onun bu listesini kullandı.
Ancak Mersenne’in listesini yayınlamasından 230 yıl sonra Edouard Lucas 2 üzeri 67 eksi 1’in, listede olmasına rağmen, asal olmadığını kanıtladı. Bugün Mersenne’in beş hata yaptığını biliyoruz. İlk olarak p = 67 ve 257 için Mersenne sayıları bileşik sayıdır. Ayrıca listede yer almayan p = 61, 89, 107 gibi üç asal sayı da Mersenne Asalıdır.
1952’de Amerikalı matematikçi Raphael Robinson bu görevi gerçekleştirecek bir bilgisayar programı yazdı. 10 ay içinde sonraki beş Mersenne asal sayısını ve bunlara karşılık gelen mükemmel sayıları buldu. Sonraki 50 yıl boyunca, hepsi bilgisayar kullanılarak, hızla yeni Mersenne asal sayıları keşfedildi.
Bilgisayarlar yeni Mersenne asal sayılarını ve bunlara karşılık gelen mükemmel sayıları bulmada inanılmaz derecede başarılı oldular ama şu ana kadar sadece 51 tane bulduk. Ancak hala tek mükemmel sayı var mı sorusuna cevap veremedik.
Buna bir cevap bulmak için yapılması gereken şey tek sayıları yazmak ve mükemmel olup olmadıklarını kontrol etmek. Matematikçiler yıllar içinde arayışlarına bazı sınırlamalar getirdiler ama yine de bir cevaba ulaşamadılar. Günümüzde varsa bu sayının 10 üzeri 3000’den büyük olması gerektiğini ve en az 10 çarpana sahip olması gerektiğini biliyoruz.
Belki de Tek Mükemmel Sayıları Aramaktan Vazgeçmeliyiz
Euler, tek mükemmel sayıların olup olmadığını belirlemenin çok zor bir soru olduğunu söylemişti ve haklıydı. Pek çok kişi, eğer gerçek dünyaya yönelik uygulamalar yoksa, o zaman üzerinde çalışmanın bir anlamı olmadığını düşünebilir. Ancak sayılar teorisindeki bir çok problemin başlangıçta gerçek dünya ile ilişkisi yoktu. Şu anda ise bu problemler güvenliğimizi sağlamada kullanılıyor. Sayılar teorisinde yapılan çalışmalar için sabır gereklidir. Tek mükemmel sayıların arayışı da buna bir örnektir. Ancak bu emeğin sonucunda elde edilen ödül tüm çabalara değebilir.
Kaynaklar ve ileri okumalar
- Mathematicians Open a New Front on an Ancient Number Problem; Kaynak site: Ouanta Magazine. Yayınlanma tarihi: 10 Mayıs 2020. bağlantı: Mathematicians Open a New Front on an Ancient Number Problem/
- Dris, Jose Arnaldo. (2023). Some new results on odd perfect numbers – Part I. 10.13140/RG.2.2.14240.35845/2.
Matematiksel