Başlıktaki soru ilk bakışta çok kolay görünüyor. Sonuçta 1-1+1-1+1-1+… şeklinde devam eden 1 ve -1’leri toplamak son derece kolaydır. Fakat Grandi serisi adını verdiğimiz bu seri, hiç de göründüğü gibi kolay değildir.
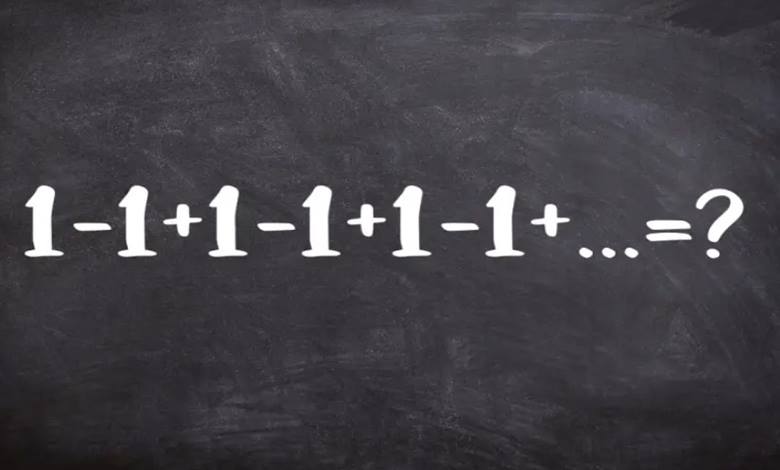
Görünüşteki basitliğine rağmen Grandi serisi, matematikteki oldukça ilgi çekici serilerden bir tanesidir. 1-1+1-1+1-1+… şeklinde sonsuza kadar devam eden bu seri, ismini İtalyan matematikçi Guido Grandi’den alır.
Grandi serisi, ıraksak serilerin klasik bir örneğidir. Iraksak seriler, yakınsak serilen aksine belli bir değere yaklaşmaz. Bu nedenle ıraksak seriler matematiksel merak ve tartışma için harika bir zemin sunar. Ayrıca Grandi serisinin bu kadar ilgi çekmesinin bir nedeni de toplamanın tartışmalı doğasıdır. Çünkü uygulanan toplama yöntemine bağlı olarak seri farklı sonuçlar vermektedir.
“Öyle şey olur mu canım, bu serinin toplamı basbayağı 0’dır” diyorsanız, okumaya devam etmenizi öneririz. Zira 1-1+1-1+1-1+… işleminin sonucu kimilerine göre 0, kimilerine göre 1, kimilerine göreyse 1/2!
Guido Grandi ve Grandi Serisinin Ortaya Çıkış Hikayesi
Guido Grandi 1671 yılında İtalya’nın Cremona kentinde doğdu. Matematikçi olmasının yanı sıra bir keşiş olan Grandi, Camaldolese tarikatının bir üyesiydi. Fakat dine olan bağlılığı akademik çalışmalarının önünde bir engel değildi. Aksine, bu sayede akademik kaynaklara ve ağlara erişimi daha kolaydı. Biraz da bu yüzden Grandi’nin çalışmaları genellikle teolojik ve matematiksel ilgilerinin iç içe geçmesiyle oluşuyordu. Bu sayede Grandi, matematiksel fenomenlere benzersiz bir bakış açısı getirmişti.

İtalyan keşiş, kendi adını taşıyan Grandi serisini ilk kez 1703 yılında incelemiştir. 1-1+1-1+1-1+… serisinde sadece parantezlerin yerini değiştirerek serinin toplamını 0 ya da 1 bulabildiğini gözlemlemiştir. Grandi bu gözlemini şu şekilde yapmıştı:
- (1 – 1) + (1 – 1) + (1 – 1) + …= 0 + 0 + 0 + …= 0
- 1 + (-1 + 1) + (-1 + 1) + (-1 + 1) + …= 1 + 0 + 0 + 0 + …= 1
Guido Grandi’ye göre serinin toplamının hem 0 hem de 1 edebilmesi teolojik bir anlam barındırıyordu. Başlangıçta 0 olan toplam sadece bir parantezin kaymasıyla 1 oluyordu. Grandi’ye göre bu durum, yoktan yaratılışın nasıl mümkün olduğunu gösteren bir kanıttı.
Grandi’nin bulguları matematik camiasında oldukça yankı yapmıştı. Bazı çağdaşları Grandi’nin vardığı sonuçları paradoksal ve saçma olarak değerlendiriyordu. Bazıları ise Grandi’nin fikirlerinin daha fazla araştırılması gerektiğini düşünüyordu. Böylece ondan sonraki matematikçiler, matematikteki yakınsama ve ıraksama kavramları üzerine derinleşerek Grandi serisine bir çözüm bulmaya çalıştı.
1-1+1-1+1-1+… İşleminin Sonucu Kesirli Olabilir mi?
Bir serinin toplamının iki farklı sonucunun olması pek kabul edilebilir bir şey değildir. Bu nedenle Grandi de dahil olmak üzere birçok matematikçi Grandi serisinin sonucunu aramıştır. Böyle bu serinin sonucuna ilişkin birçok yorum ortaya atılmıştır.
1-1+1-1+1-1+…. işlemi için en kabul gören sonuçların başında 1/2 cevabı gelir. Grandi ve ondan sonra gelen birçok 18. yüzyıl matematikçisi cevabın 1/2 olduğunu savunmuştur. Ama tam sayıların toplamından oluşan bir serinin cevabı neden 1/2 olsun ki?
Grandi cevabın 1/2 olmasını şu şekilde özetliyor: İki kardeşe babalarından tek bir tane mücevher miras kaldığını hayal edin. Her iki kardeş de bu mücevheri dönüşümlü olarak kendi evinde sakladığını düşünün. Eğer bu mücevher iki kardeşin çocukları arasında da devredilecek olsaydı, bu ailelerin mücevher üzerindeki mülkiyet hakları 1/2 olurdu.

Ünlü matematikçi G. W. Leibniz ise Grandi’nin bu açıklamasına katılmış ancak bunu olasılıksal akıl yürütmeyle doğrudan desteklemeye çalışmıştır. Bu noktada Leibniz, serileri rastgele bir noktada toplamayı bıraktığımızda o noktaya kadar olan toplamın eşit olasılıkla 0 ya da 1 olacağını, bu nedenle bunların ortalaması olan 1/2’yi cevap olarak almanın mantıklı olacağını savunmuştur. Her ne kadar Leibniz sonucun doğru olduğunu düşünmüşse de argümanının matematiksel olmaktan çok metafiziksel olduğunun farkındaydı.
Bir diğer ünlü matematikçi Leonhard Euler ise 1/2 cevabını savunmak için daha karmaşık yöntemler kullanmıştır. 1760 tarihli De Seriebus divergentibus (Farklı Seriler Üzerine) adlı makalesinde 1-1+1-1+1-1+… ile 1/2 kesrinin eşdeğer nicelikler olduğunu ve birini diğerinin yerine her daim koyabileceğimiz konusunda hiçbir şüpheye yer olmadığını iddia etmiştir.
Cesàro ve Abel Toplamlarına Göre Grandi Serisinin Toplamı Kaçtır?
Bunun için öncelikle matematikteki ıraksama ve yakınsama kavramlarına bakmamız gerekir. 1-1+1-1+1-1+… gibi bir seride kısmi toplamların dizisi sonlu bir limite yakınsamıyorsa, sonsuz serimiz ıraksak demektir. Grandi serisi de ıraksak serilere bir örnektir.
Grandi serisinin kısmi toplamlarını incelediğimizde değişen bir model gözlemleriz. İlk kısmi toplam 1, ikincisi 0, üçüncüsü yine 1’dir ve bu böyle devam eder. Bu durum serinin tek bir sonlu değere yakınsamadığını gösterir. O nedenle de seri ıraksak olarak sınıflandırılır.
Iraksak olmasına rağmen matematikçiler bu tür serileri sonlu değerler atamaya çalışmıştır. Bunu yaparken kullandıkları yöntemlerden biri de Cesàro toplamasıdır. Cesàro toplamasında serilerin kısmi toplamlarının ortalamasını dikkate alırız.
Grandi serisi için düşünecek olursak Sn, n’inci kısmi toplamsa Cesàro toplamı n sonsuza yaklaştıkça bu kısmi toplamların ortalamasının limitidir. Bu durumda kısmi toplamlar dizisi 0 ile 1 arasında değişir. Ve n çok büyüdükçe 1/2’ye yaklaşan (0+1+0+1+…)/n ortalamasını verir. Böylece, Cesàro toplamı Grandi Serisine 1/2 değerini atar.

Grandi serisinin sonucuna ilişkin bir diğer teknik de seriyle ilişkili kuvvet serisini dikkate almayı ve değişken belli bir limite yaklaştıkça davranışını inceleyen Abel toplamıdır. Abel toplamında Grandi serisi için 1 – x + x2 – x3 + x4 -… kuvvet serisini alıyoruz ve x soldan 1’e yaklaştıkça toplamına bakıyoruz. Bu kuvvet serisi 1/(1+x) olarak ifade edilebileceğinden 1/2’ye yakınsar. Bu yüzden Abel toplamı da Grandi serisinin toplamına 1/2 der.
Grandi Serisinin Günlük Hayattaki Yeri ve Önemi
1-1+1-1+1-1+… ile ifade edilen Grandi serisi sadece matematiksel bir merak ürünü değildir. Bu serinin çeşitli disiplinlerde derin etkileri vardır. Grandi gibi ıraksak serilerin anlaşılması teorik fizik, sinyal işleme ve bilgisayar bilimi gibi alanlarda son derece önemlidir.
Teorik fizik alanında bakacak olursak ıraksak seriler, kuantum alan teorisi ve sicim teorisinde karşımıza çıkar. Grandi serisi gibi seriler burada renormalizasyon sürecine yardımcı olur. Böylece fizikçiler görünüşte paradoksal olan sonsuz toplamlardan sonlu ve anlamlı sonuçlar elde eder.
Sinyal işlemedeyse Grandi serisi sinyallerin analizi ve manipülasyonu sırasında karşımıza çıkar. Iraksak serilerin anlaşılmasından türetilen teknikler gürültü azaltma ve sinyal iyileştirme algoritmalarında kullanılır.
Bir diğer alan olan bilgisayar bilimlerindeyse özellikle algoritma tasarımı ve analizi alanında ıraksak serilerden yararlanılır. Bu serilerin davranışını anlamak büyük veri kümelerini daha etkili bir şekilde işleyen optimize edilmiş kodların oluşturulmasını sağlar.
Kısacası Grandi serisinden türetilen kavramlarının birçok pratik uygulaması olduğunu söylemek mümkündür. Bu nedenle 1-1+1-1+1-1+… gibi basit görünümlü bir serinin geniş kapsamlı incelenmesi saf matematiğin ötesinde, geniş kapsamları etkilere sahiptir.
Yazının devamında göz atmak isterseniz: Ramanujan Toplamı: 1+2+3+4+…= -1/12 İfadesi Nedir?
Kaynaklar ve İleri Okumalar
- The Paradox of 1 – 1 + 1 – 1 + 1 – 1 + … ; Bağlantı: The Paradox of 1 – 1 + 1 – 1 + 1 – 1 + … | Scientific American ; Yayınlanma tarihi: 16 Ağustos 2024
- Grandi’s series ; Bağlantı: Grandi’s series – Wikipedia
- Grandi’s Series: Exploring the Sum of 1−1+1−1+1−1… ; Bağlantı: Grandi’s Series: Exploring the Sum of 1−1+1−1+1−1… (diversedaily.com)
Matematiksel