19. yüzyılda “kuaterniyonlar – dördey” adı verilen sayıların keşfi, matematikçilere uzaydaki dönüşleri tanımlamanın bir yolunu vererek fizik ve matematiği sonsuza dek değiştirdi.
Yeni geometrilerin icadından önce, insanlar matematiğin benzersiz ve evrensel olarak doğru bir bilgi sistemi olduğuna inanıyorlardı. Yanılıyorlardı. Matematik bir değil, çoktu. Ve yeni geometriler göz önüne alındığında, fizikçiler yavaş yavaş eski geometrinin doğanın kesin tanımı için en iyi araç olmadığını kabul etmek zorunda kaldılar. Sonunda Einstein, teorisini geleneksel olmayan bir geometri kullanarak formüle etti.
Benzer bir durum matematik için de geçerli idi. “Gerçek sayılar” aşina olduğumuz tüm sayılardır. Gerçek sayıları toplayabilir, çıkarabilir, çarpabilir ve bölebiliriz ve bunları hem sınıflarda hem de günlük hayatımızda soruları cevaplamak için kullanabiliriz.. Ancak gerçek sayılar tüm matematik problemlerimizi çözmek için yeterli değildir.
Kuaterniyonlar Fikri Nasıl Doğdu?
x2=1 denklemini çözmek kolaydır. Cevabın x=1 veya x=-1 olduğunu kolayca anlayabilirsiniz. Sıra x2=-1 denklemine geldiği zaman işler biraz garipleşir. Çünkü bu sorunun cevabının -1’in karekökü diğer deyişle x=√ -1 biçiminde olur. Bu da bizi sanal sayılar fikrine götürecektir. -1’in karekökünü içeren sayılara da karmaşık sayılar denir.
Cardano bu gerçek olmayan sayılara tereddütle yaklaştı, hatta onlarla yaptığı aritmetiği işe yaramaz olarak tanımladı. Ancak gerçek sayılarla aynı kuralların çoğuna uyduklarını görünce şaşırdı. Ve biraz zaman alsa da, Cardano’nun √ -1 ‘i gönülsüzce kullanması, gerçek sayıların güçlü ve üretken bir uzantısı olan “karmaşık sayılar”ın geliştirilmesine yol açtı.
Karmaşık sayılarda da normal sayılarda yaptığımız bir çok işlemi yapabilirsiniz. Toplamak ve çıkarmak için, gerçek kısımları ve sanal kısımlar ile kendi aralarında işlem yapmanız yeterlidir. Karmaşık sayıların çarpımı da, dağılma özelliği yardımı ile yapılır ve elde edeceğiniz sonuç yeni bir karmaşık sayı olur. Peki ama neden burada duralım ki?

Hamilton, 16 Ekim 1843 Pazartesi günü, Kraliyet Ailesi’nin bir Konsey toplantısına başkanlık yapmak için Kraliyet Kanalı boyunca eşiyle birlikte yürürken matematikteki en ünlü vandalizm eylemini gerçekleştirdi. O esnada tam da Brougham Köprüsü’nün üzerindeydi.
Kalemini çıkardı ve oradaki taşa aklına gelen formülü çizdi. Yazdığı formül şu şekildeydi: i2 = j2 = k2 = ijk = –1. Buluşunu “kuaterniyonlar” ( dördey) olarak adlandırdı.

Hamilton’un kuaterniyonları icat etmesinin ardından, matematikçiler yeni cebirler icat edebileceklerini fark edeceklerdi. Kuaterniyonlar, garip özelliklere sahip yeni bir sayı türüydü. Bu sayılar sadece bir değil birden fazla sanal kısma sahipti. Üstelik matematiğin geleneksel “yasalarından” bazıları kuaterniyonlar için geçerli değildi. Ancak yine de teori, mevcut cebir kuralları ile uyumluydu.
Kuaterniyonlar Nedir?
Bir kuaterniyon q ile gösterilmek üzere q=a + bi + cj + dk şeklinde yazılabilir. Burada a, b, c ve d gerçek sayılar ve i, j ve k ise sanal sayılardır. Yani karşılıkları √-1 ‘dir. Bu dörtlüyü kısaca (a, b, c, d) biçiminde gösterebiliriz.
Buradaki i, j ve k sanal sayılar olmasına rağmen her birinin vektörel anlamda anlamları birbirinden farklıdır. Gerçek ve karmaşık sayılarla yapabileceğiniz her şeyi, bir çarpıcı fark dışında, kuaterniyonlarla da yapabilirsiniz. 2 × 3 ve 3 × 2’nin her ikisi de 6’ya eşitken, kuaterniyon çarpımında sıra önemlidir.
Karmaşık sayılar, hayal gücünün tuhaf figürleri değildir. Aslında kendi başlarına geometrik anlamları da vardır. Koordinatları (x,0) olan yatay eksende bulunan sayıları düşünün. Onları -1 ile çarpmak onları (0,0) noktasının diğer tarafına çevirecektir. Yani (1,0) noktasını -1 ile çarparsanız (-1,0) noktasını elde edersiniz. Bu nedenle -1 ile çarpmayı 180 derece döndürme olarak düşünebilirsiniz.
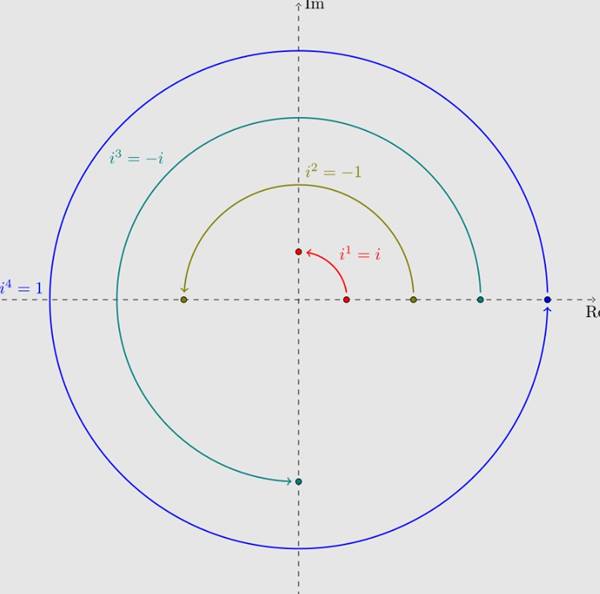
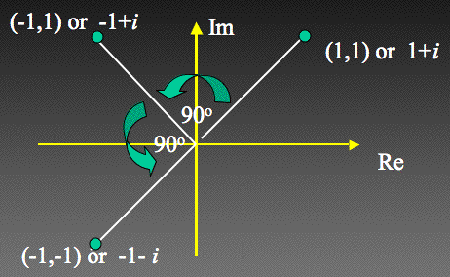
Şimdi i ile çarpmaya ne dersiniz? Herhangi bir karmaşık sayıyı i ile çarptığımız zaman aslında sayımızı söndürmüş oluruz. Örneğin 1+i sayısının i ile çarpımı bize -1+i sonucunu verecektir. Ancak bu eylemi iki boyutlu olarak gerçekleştiririz. Aslında, yalnızca 90 derecelik değil, herhangi bir döndürme, karmaşık bir sayı ile çarpma kullanılarak elde edilebilir.
Kuaterniyonlar Ne İşe Yarar?
Kuaterniyonlar çok sayıda fiziksel uygulamayla ilişkilidir. Karmaşık bir sayı, iki boyutlu bir düzlemdeki noktaları temsil ederken, bir kuaterniyon, üç boyutlu uzaydaki noktaları tanımlar. Işık hızına yaklaştıkça uzunlukların nasıl kısaldığını ve zamanın nasıl genişlediğini açıklayan Lorentz dönüşümleri kuaterniyonları kullanır.
Her ne kadar kulağa soyut bir kavram gibi gelse de kuaterniyonlar, akıllı telefonunuzun ve tabletlerinizin dönüşünü programlamak için de kullanılır. Üstelik burada da bitmez. Gerçek sayıların ötesindeki bu uzantılar, Hamilton’un meslektaşları tarafından keşfedilen ve yedi sanal birime sahip daha da garip bir sayı sistemi olan sekiz boyutlu oktonyonlarla devam eder.
Oktonyonlar sekiz ayrı birim sayının lineer kombinasyonu olarak ifade edilen hiperkompleks sayılardır. Daha basitçe söylememiz gerekirse bunlar sekiz boyutlu uzaydaki noktalardır. Bu sayılar bize farklı boyutlara kapı açar. Ancak bunun karşılığında da bir ödün vermemiz gerekir. Çünkü bu sayılar da hem değişme hem de birleşme özelliğini sağlamaz.
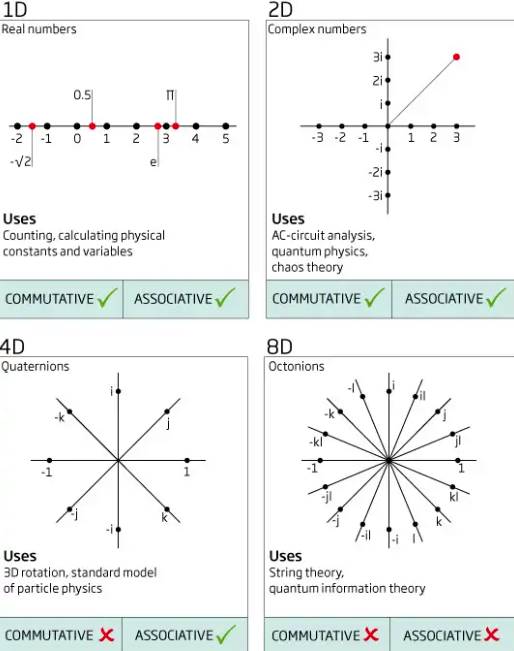
Gerçek sayıları genişleterek yarattığımız bu sistemler ile her adımda gerçek olarak düşündüğümüz şeyle de bağımızı kaybedebiliriz. Ancak kazandığımız şey, dünya hakkında düşünmenin yeni yollarıdır. Ve bunun için her zaman bir kullanım alanı bulabiliriz. Hamilton fikirlerini bir köprüye karalamış olabilir ancak bunlar belki de çoktan kozmosun dokusuna işlenmiştir.
Kaynaklar ve ileri okumalar:
- The Many Modern Uses of Quaternions; Yayınlanma tarihi: 4 Ocak 2016; Bağlantı: https://thatsmaths.com/
- The Strange Numbers That Birthed Modern Algebra. Yayınlanma tarihi: Kaynak site: Quanta Magazine. Bağlantı: The Strange Numbers That Birthed Modern Algebra
- Maths goes to the movies; yayınlanma tarihi: 24 Kasım 2017; Bağlantı: https://plus.maths.org/content/maths-goes-movies-0
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel







Derli toplu ve faydalı yazınız için çok teşekkürler.
Rica ederim. Keyifli okumalar :)