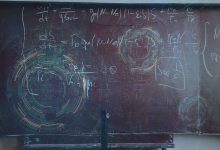İdealist bir öğretmen ve akıllıca düşünülmüş bir matematik sorusu eşliğinde Pisagor sayılarını öğrenelim.
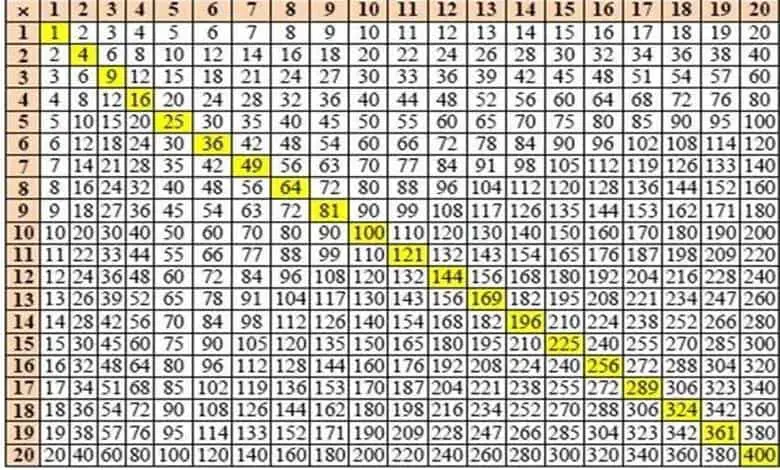
Matematikte bir çoğumuzun aklından en çok kalan teoremlerin başında Pisagor Teoremi gelir. Her ne kadar ilk kendisi formüle etmese de günümüzde Pisagor adıyla hatırlanan bu teorem bize, bir dik üçgende kenarların karelerinin toplamının hipotenüsün karesine eşit olduğunu söyler. Cebirsel olarak da, a ve b kenarlar olmak üzere, a2 + b2 = c2 biçiminde gösterilir. Burada c hipotenüsü temsil eder.
Pisagor teoremini öğrendikten sonra da Pisagor üçlüleri ile tanışırız. Kuşkusuz ki bu üçlüler arasında en çok akılda kalan 3, 4 ve 5 sayılarıdır. Bir Pisagor üçlüsünde en büyük sayı hipotenüstür. Hipotenüsü 100’den küçük olan bazı Pisagor üçlüleri ise yukarıdaki gibidir.

Listeye dikkatle bakarsanız kırmızı ve mavi ile yazılmış olan bazı üçlülerin birbirinin katı olduğunu fark edersiniz. Geometrik olarak, eğer bir Pisagor üçlüsü diğerinin katıysa, karşılık gelen üçgenler benzerdir. Bir Pisagor üçlüsü başka bir Pisagor üçlüsünün katı değilse, o zaman bunun temel üçlü olduğunu söyleriz. Örneğimizde (3, 4, 5) temel bir Pisagor üçlüsü iken (6, 8, 10), (9, 12, 15) ve (12, 16, 20) değildir.
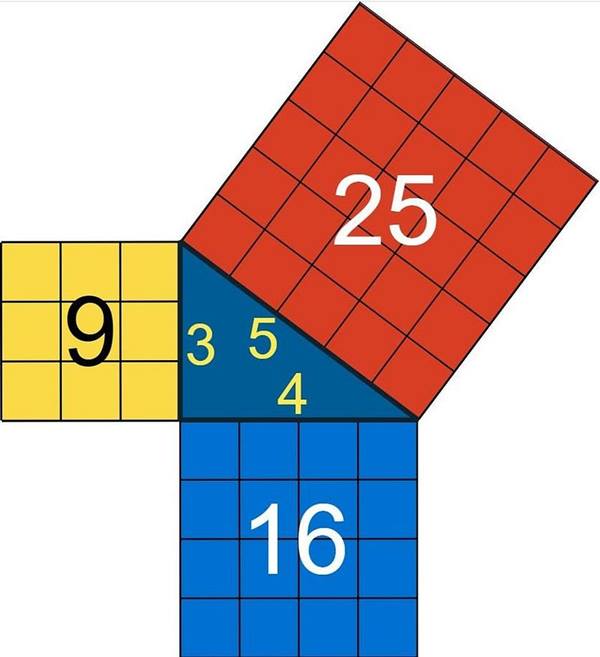
Pisagor üçlüleri arasında 3, 4 ve 5 özel bir yere sahiptir. Bunun nedeni Pisagor Teoremine uyan ardışık tam sayılar olmalarıdır. Aslında a ² + b² = c ² denklemini sağlayan başka ardışık sayı olmadığını görmeniz mümkündür. Şimdi kenarlarımızdan birine b diyelim. Şimdi a, b ve c’nin ardışık sayılar olmasını istiyorsak a ve c kenarlarını b cinsinden yazmamız gerekecektir. Bu nedenle c= b + 1 ve a= b-1 olsun.
Bundan sonrasında yapmamız gereken tüm bunları denklemde yerine yerleştirmek ve çözmektir. Denklemimiz ( b - 1)² + ( b )² = ( b + 1)² biçiminde olacaktır. Buradan da b² – 4b = 0 sonucunu elde ederiz. Yani b’nin ya 0 ya da 4 olması gerekir. Sonucunda b sıfır olamaz bu durumda b=4 olmalıdır. Bu sonucumuzu yerine yazarsak da 3² + 4² = 5² eşitliğini elde ederiz.
Pisagor Teoreminine Sezgisel Yaklaşmak İlginç Sonuçlar Elde Etmemizi Sağlar.
Şu ana kadar size aktardıklarımız size zaten bildiğiniz şeyleri anlattığımızı düşünmenize neden olmuş olmalıdır. Peki ama neden kendimizi sadece 3 sayı ile sınırlayalım ki? Mesela a² + b² + c² = d² + e² veya a² + b² + c² + d² = e² + f² + g² için bu eşitlikleri sağlayan ardışık tamsayılar bulmamız mümkün olabilir mi? Bu sorunun cevabını merak ediyorsanız öncelikle aşağıdaki resme dikkatle bakın.

On dokuzuncu yüzyılın sonunda, Rus ressam Nikolai Petrovich Belsky (1868–1945), 1895 yılında “Mental Arithmetic. In the People’s School of SA Rachinsky” isimli bu tablosunu tamamladı. Resim, 19. yüzyılın sonlarına ait bir köy okulunu ve bu okuldaki bir aritmetik dersini tasvir ediyordu. Resimdeki öğretmen ise Sergei Alexandrovich Rachinsky (1833-1902) idi.
Tahtada yazılan bir soru üzerine düşünen ve kafalarından hesap yapmaya çalışan öğrencileri görüyoruz. Yüz ifadelerine bakıldığı zaman bu öğrencilerin soru karşısında zorlandıklarını görmek de mümkün. Aslında resme daha dikkatli bakıldığı zaman tahtada gerçek bir matematik sorusu yazıldığı görülüyor. Tahtadaki soru aşağıdaki gibi.
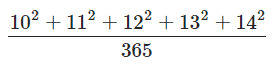
Hesap makinesi olmadan bu soruyu çözmeye çalıştığınızı hayal edin. Kesinlikle yapılabilirsiniz ancak bu biraz zaman alıcıdır. Bununla birlikte, sayılar arasında var olan ilişkiler sayesinde, sorunun cevabını çok kısa sürede yapmanız mümkündür. Hatta bu ilişkiyi anladıktan sonra siz de başka rakamlar ile başka sorular oluşturabilir ve etrafınızda aynı şaşkınlığı yaratabilirsiniz.
Tahtadaki soruyu aşağıdaki gibi düşünürsek, çözümü sağlayan tek sayının 12 olduğunu kolayca görebiliriz. ( Zamanınızı almamak adına çözüm detaylarına girmeyeceğiz. Ancak eşitliğin parantezleri açıp, gerekli sadeleştirmeleri yaparsanız denklemi sağlayan tek sayının 12 olduğunu göreceksiniz.)
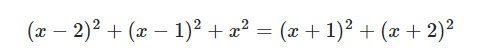
Gördüğünüz gibi resim aslında oldukça akıllıca düşünülmüş bir matematik sorusu içermektedir. Peki bu matematik sorusundan yola çıkarak bir genelleme yapabilir miyiz? Şimdi cebirsel gösterimden geometrik gösterime geçelim. Pisagor denklemimize yani a2 + b2 = c2 eşitliğimize geri dönelim.
Pisagor Sayıları İle Tanışın
Öncelikle aşağıdaki mavi kare bir kenarı b olan bu kareyi temsil etsin. Şimdi bu b karesinin bir kenarını 1 birim genişliğinde parçalara bölelim. Sonrasında da (b-1) karesinin ( sarı renkli olan) her kenarına böldüğümüz bu parçaları ekleyelim. Son durumda elde ettiğimiz karenin ( yeşil olan) bir kenarı (b+1) kadar olacaktır.
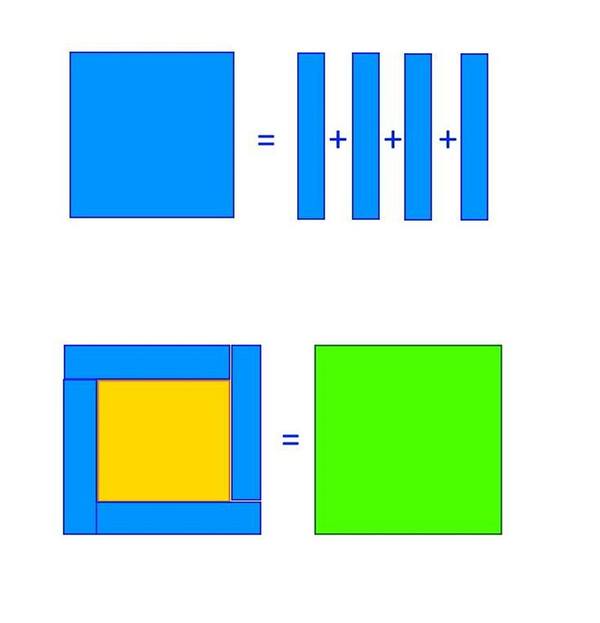
Şimdi yaptığımız işlemi genelleyelim. Elimizde 3 kenar varsa, ortada olanın bir kenarını 1’er birimlik parçalara bölersek, sonrasında da bunu kısa olan kenara eklersek, uzun olan karenin bir kenarını elde edebiliyoruz. Şimdi aynı mantığı 10² + 11² + 12² = 13² + 14² için yapalım. Bu sefer de tam ortadaki kenar uzunluğunu (12) bir birim uzunluğunda parçalara böleceğiz.
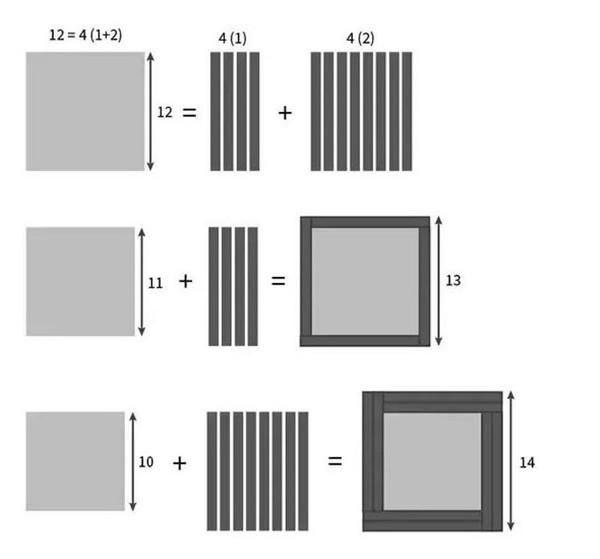
Ancak bu sefer elimizde daha büyük hale getirmemiz gereken iki tane karemiz var. Bu nedenle bu parçalardan 4 tanesini bir küçük olan yani 11 birimlik karenin kenarlarına ekleyeceğiz. [Bu durumda (x-1)’i ( x+1) yapmış olduk]. Diğer kalan 8 tanesini de en küçük olanın kenarlarına iki defa ekleyeceğiz. [Bu durumda (x-2)’yi ( x+2) yapmış olduk.] Ancak bu hile sadece ortadaki sayı 12 olduğu için işe yarar.
Bu noktada matematiksel açıdan ilginç bir örüntünün ortaya çıkmaya başladığını fark etmiş olabilirsiniz. Şimdi a² + b² + c² + d² = e² + f² + g² denkleminin çözümünü nasıl bulacağımıza bakalım. Bu sefer ortadaki terimimiz yani bir birimlik parçalara ayıracağımız karemizin bir kenarı d. Şimdi aşağıdaki görsel bize bir yol haritası çizecektir.
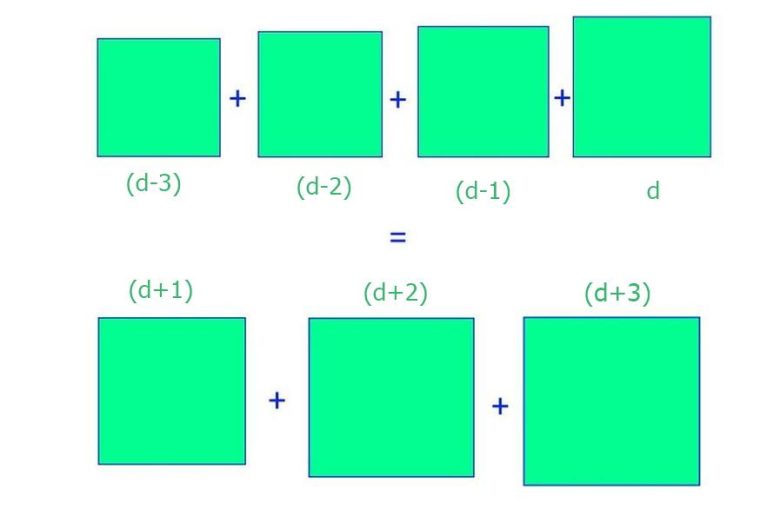
Bize (d-1) karesini (d + 1) karesine dönüştürmek için 4 parça; (d-2) karesini (d+2) karesine dönüştürmek için 8 parça ve (d-3) karesini (d + 8) karesine dönüştürmek için 12 parça gerekecektir. Bu durumda da ortadaki karenin uzunluğunun d=4 + 8 + 12 = 24 olması gerekecektir. Yani 21² + 22² + 23² + 24² = 25² + 26² +27² sonucunu elde ederiz. Sonucu aşağıdaki çizimde de inceleyebilirsiniz.
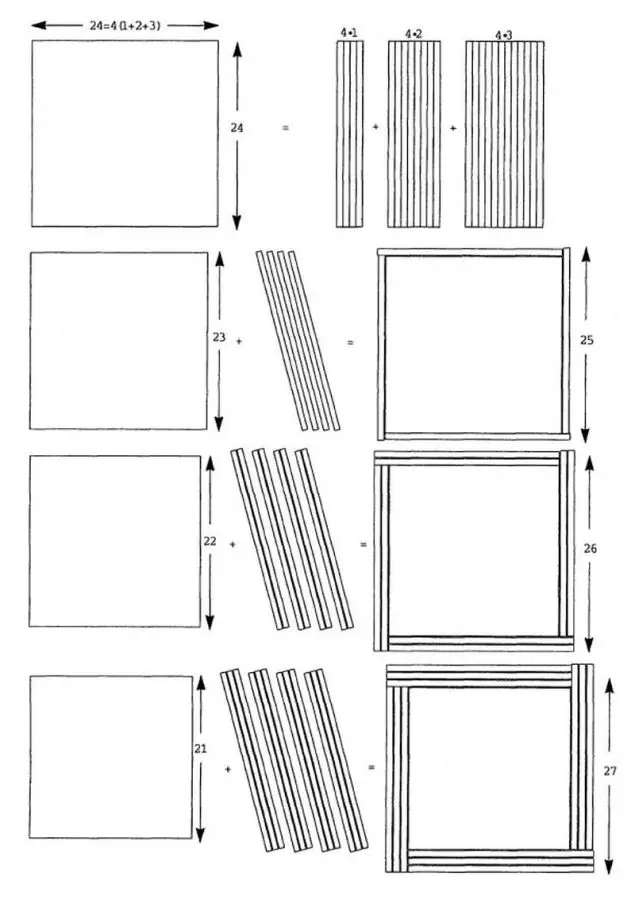
Sonuç Olarak;
Ortadaki sayıyı bu biçimde hesaplamaya devam ederek hesaplamaları istediğimiz kadar uzatabiliriz. Ortadaki sayılara ise yani 4, 12, 24, 40, 60, 84, 112 vb. gibi sayılara Pisagor sayıları denir. Pisagor işe a2 + b2 = c2 ile başlamıştı. Ve bunu sağlayan ardışık sayıların (3, 4, 5) olması gerektiğini göstermişti.
Gördüğünüz gibi cebir yerine geometrik yaklaşım kullanarak a² + b² + c² = d² + e² için gerekli ardışık sayıların (10, 11, 12, 13, 14) ve a² + b² + c² + d² = e² + f² + g² için ise (21, 22, 22, 23, 24, 25, 26, 27) olduğunu bulduk.

Peki ama bu bizim ne işimize yaradı diyeceksiniz. Pisagor sayılarının sayılar kuramında çeşitli uygulama alanları vardır. Resimdeki çocukların bunu bilmesi elbette mümkün değildi. Ancak öğretmenlerinin önemli bir matematikçi olduğu düşünülünce, bu soruyu tahtaya yazmasının belli bir amacı var gibi gözüküyor.
Kaynaklar ve ileri okumalar
- This One Equation, 10² + 11² + 12² = 13² + 14², Takes Pythagoras. To A Whole New Level. Yayınlanma tarihi: 13 Mart 2020. Bağlantı: This One Equation, 10² + 11² + 12² = 13² + 14², Takes Pythagoras. To A Whole New Level
- Michael Boardman (2000) Proof Without Words: Pythagorean Runs, Mathematics Magazine, 73:1, 59, DOI: 10.1080/0025570X.2000.11996805
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel