Matematikte zaman zaman karşımıza beklemediğimiz durumlar da çıkar. Bunlardan bir tanesi 1951 yılında Alfred Moessner tarafından keşfedildi. Aynı yıl bu keşfin geçerliliği Oskar Perron tarafından gösterildi. Bu keşif günümüzde Moessner teoremi ancak daha çok Moessner mucizesi adı ile biliniyor. Bir mucizeyi öğrenmek istiyorsanız okumaya devam ediniz.

Muhtemelen bir çok kişi ardışık pozitif tek sayıların toplamı ile ilgili 1 + 3 + 5 + … + (2n – 1) = n 2 formülüne aşinadır. Aslında bu toplamı istersek geometrik olarak aşağıdaki gibi de gösterebiliriz. Bu sayede ispata gerek kalmadan şekle bakarak nedeni fark etmeniz mümkün olacaktır.
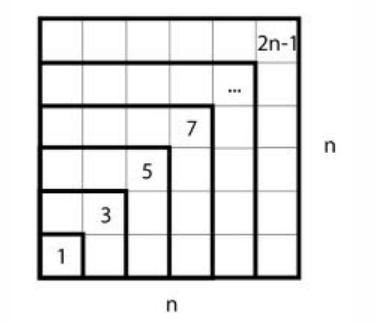
Aslında yukarıda gördüğünüz ispat Pisagor tarafından yapılmıştı. İnsanlar bu ispatı o kadar çok sevmişti ki uzun süre yeni bir arayış içine girmediler. Ancak yaklaşık 70 yıl önce Alfred Moessner bu ispata farklı bir biçimde bakınca işler değişecekti. Alfred Moessner olaya farklı bir bakış açısı ile yaklaştı ve bulgularını 1951 yılında yayınladı. Ancak yayın dili Almanca olduğu için çalışması, fazla da kimsenin başlangıçta dikkatini çekmedi.

Alfred Moessner Tam Olarak Ne Yapmıştı?
Alfred Moessner, en sevdiğimiz dizilerden bazılarının şaşırtıcı ve yeni bir yolla bulunabileceğini keşfetti. Gelin şimdi onun gibi düşünmeye çalışalım. Önce yanyana sayma sayılarını yazalım. Ardından da her ikinci sayıyı daire içine alalım. Sonrasında da daire içine alınmamış sayıların kümülatif toplamlarını bulalım. Eğer dikkat ederseniz bulduğunuz sonuç tam kareler olacaktır.

Bu bulduğumuz sonuç sonuçta yukarıda elde ettiğimiz ile aynı. Bu size fazla cazip gelmemiş olacaktır. Ancak Moessner burada durmayacaktı. Şimdi sayma sayılarını bir kere daha sıralayalım. Ancak bu sefer her 3 sayıda bir rakamları daire içine alalım.
Sonrasında da o rakama o kadar olan, daire içine alınmamış olan sayıların toplamlarını bulalım ve altlarına yazalım. Yani ikinci satırda bir dolu bir boş biçiminde, her ikinci sayıyı yuvarlak içine alalım. Sonrasında da kalan sayıları toplayıp altına yazalım. Sonuçta bir şey fark ettiniz mi?
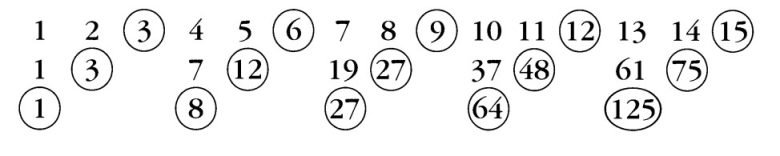
Evet sizin de fark ettiğiniz gibi elde ettiğimiz sayılar, yani 1, 8, 27, 64, 125 sırasıyla 1, 2, 3, 4 ve 5 sayılarının küpüdür. Muhtemel bu güne kadar kimse pozitif tam sayıların küplerini elde etmek için bu yöntemi düşünmemiştir.
Moessner Mucize Teoremi Ortaya Çıkıyor
Aslında bu noktada durmak zorunda değiliz. Aynı işlemi bu sefer her dört sayıda bir yuvarlak içine alıp, ardından da yuvarlak içine almadığımız sayıları toplarsak ne elde edeceğimize bakalım. İlk satırda her 4 sayıda bir, ikinci satırda her üç sayıda bir, üçüncü satırda her iki sayıda bir yuvarlaklarımızı çizdik. Sonrasında da yuvarlaklara kadar olanları toplayıp altlarına yazdık. Ne fark ettiğiniz? Evet gördüğünüz gibi elde ettiğimiz 1, 16, 81 ve 256 sayıları; 1, 2, 3 ve 4 sayılarının 4. kuvveti.
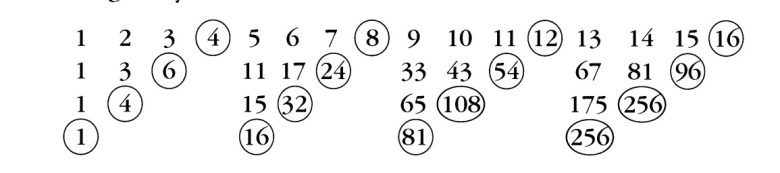
Bu durumda artık genelleme yapabiliriz. Ancak öncesinde son bir çalışma daha yapalım. Bu sefer 1 + 2 + 3 + … + n toplamını bulmaya çalışalım. Yani aşağıda da göreceğiniz gibi öncelikle 1, ardından 2, ardından 3 sayı atlayarak bir sonraki sayıyı yuvarlak içine alalım. Sonrasında da her satırsa yuvarlak içine almadıklarımızı toplayalım.
Bu sefer ne fark ettiniz? Evet 2=2!; 6=3!; 24=4!; 120=5!…Sonuçlarımız giderek daha ilginç olmaya başladı. Moessner mucizesi sayesinde sayıların faktöriyellerini nasıl hesaplayabileceğimizi gördük.
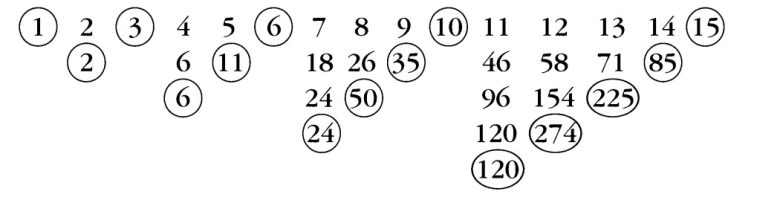
Bu Teoremin Bir İspatı Var mı?
Sonuç olarak Moessner Teoremi bize şunu der: Öncelikle pozitif tam sayıları sıralayıp ardından bu sayılardaki her n. terimi diziden çıkaralım ( Yani yuvarlak içine alalım) ve kalanların kısmi toplamlar dizisini bulalım. Ardından kısmi toplamlar dizisinin her (n-1). terimini diziden çıkaralım ve yine dizinin kısmi toplamlarını hesaplayalım. Bu şekilde yöntemi devam ettirdiğimizde elde edeceğimiz son dizi, pozitif tam sayıların n. kuvvetleri olacaktır
Yazımızı bu noktaya kadar okuduysanız neler olup bittiğini merak etmiş olmalısınız. Aslında Moessner’in de bilip bilmediğinden emin değiliz. Sonucunda sadece 1 sayfadan oluşan çalışmasında herhangi bir ispat mevcut değildi.
Elbette yıllar içinde matematikçiler bu ilginç teorem ile uğraşmaya başladı. Sonucunda matematikçi Oscar Perron bir ispat bulmayı başardı. Ancak bu ispat bir web sitesinde anlamlı bir biçimde aktarılamayacak kadar karışıktı. Aslında bu güne kadar başka da bir ispat bulunamadı. ( Kaynaklar arasından erişeceğiniz bir videoda görsel bir ispat mevcuttur.)
Matematikçiler farklı ispatlar ararken sizler de Moessner mucizesini denemeye başlayabilirsiniz. Sayıların kuvvetleri veya faktöriyeller dışında bu sayı dizisinin farklı özellikler de sakladığı düşünülüyor. Denemenin eğlenceli olacağını düşünüyoruz. Yazıdan sonra okumaya devam etmek isterseniz: Hesap Makinesinden Hızlı Toplama Yaparak Arkadaşlarınızı Şaşırtın!
Kaynaklar ve ileri okumalar
- J. H. Conway and R. K. Guy, 1996: Moessner’s magic. In The Book of Numbers, pages 63–65. Springer-Verlag.
- Moessner’s Magical Method; yayınlanma tarihi: 14 Temmuz 2019; Bağlantı: https://thatsmaths.com/
- Moessner’s theorem; bağlantı: https://en.wikipedia.org/wiki/Moessner%27s_theorem
- The Moessner Miracle. Why wasn’t this discovered for over 2000 years?; Yayınlanma tarihi: 17 Temmuz 2021; Bağlantı: https://www.youtube.com
Matematiksel