Günümüzde kullandığımız rakamların kökeni hakkında önemli bir bilgi verdiğini iddia eden aşağıdaki görseli bir yerlerde görmüş olmanız olasıdır. Bu görseldeki iddia, her rakamın aslında sahip olduğu açı sayısı ile ilişkili olmasıdır. Yani sekiz sayısında sekiz tane açı vardır ve bu nedenle de adını sekiz denmiştir. Harika bir bilgi değil mi? Elbette harika olabilirdi. Ancak ufak bir sorun var. Bu bilgi kesinlikle yanlış.
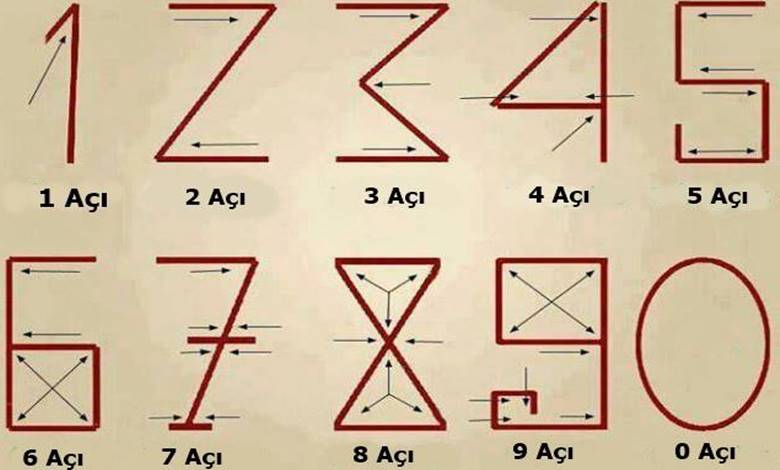
İşin üzücü tarafı yanlış olmasına rağmen hem ülkemizde hem de sınırlarımız dışında bu veya buna benzeyen gönderiler sosyal medyada sıklıkla karşımıza çıkıyor. Basit bir açıklama olması ve kulağa ilginç gelmesi nedeniyle de özellikle matematik ile fazla ilgisi olmayan kişiler tarafından kolayca kabul görebiliyor. Aşağıda onlarca defa karşılaştığımız paylaşımlardan bir tanesini görebilirsiniz.

Sayılar binlerce yıl boyunca dostumuz olmuştur. Onları keşfetmemiz taşı yontmaya başlamamızla aynı zamana denk düşse de, bugün alışık olduğumuz biçimlerine kavuşmaları uzun zaman almıştır. Yani hiç kimse sayıları bir gecede belli kuralları ortaya koyarak yaratmamıştır.
Sayılar biz değişip geliştikçe, bugün dünyaya hükmeden katı biçimlerine kavuştu. Babilliler, Çinliler, Mayalar, Mısırlılar, İbraniler ve Yunanlılar ve daha bir çok kültür kendi sayı sistemini geliştirdi. Ancak nedense onları belli kalıplara uydurmaktan evrensel olarak keyif alıyoruz gibi gözüküyor. İşte size bir örnek daha

Günümüzde Kullandığımız Rakamların Kökeni Nedir?
Rakamların gelişiminin ilginç bir geçmişi vardır. Hatta bu tarihi anlatmak için ciltler dolusu kitap yazılmıştır. Ancak bunun geometri ile herhangi bir bağlantısı yoktur. Öncelikle günümüzde kullandığımız rakamlar yani 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 simgelerini içeren rakam sistemi, Hint-Arap rakamları (Hindu-Arabic numerals / figures) olarak adlandırılmaktadır. Bu rakamların dünya genelinde Hint – Arap rakamları olarak bilinmesinin nedeni de ilk olarak Hindistan’da şekillenmiş ve daha sonra Arap matematikçiler tarafından Batıya tanıtılmış olmasıdır.
Hindistan’da matematik, MS 1. binyılın ilk yüzyıllarında hızla ilerledi. Bu rakamların kökeni ise Hintli matematikçi Aryabhata’nın ve çağdaşlarının çalışmalarına dayanıyor. 476-550 yılları arasında yaşayan Aryabhata Hint matematiğinin altın çağının ilk matematikçilerinden ve astronomlarındandır.

Yukarıda gördüğünüz Bakhshali el yazması, 1881’de Mardan, Bakhshali köyünde (günümüz Pakistan’ında Peşaver yakınında) bulunan huş ağacı kabuğu üzerine yazılmış eski bir Hint matematik metnidir. Hint matematiğine dair günümüze ulaşan en eski metin olarak kabul görmektedir. El yazması çeşitli problemlerden ve bunların açıklamalarından oluşmaktadır.

Yukarıda ise bu el yazmasında kullanılan rakamları görüyorsunuz. Hint matematikçileri bizim bugün kullandığımız rakamların orijini olan eski Brahmi rakamlarını kullanırlardı. Kullanılan sayı sisteminde Hint alfabesindeki 33 sessiz harfe sayısal değerler verilmekteydi. Gördüğünüz gibi Sanskritçe tabanlı olan bu rakamların açılar ile herhangi bir bağlantısı bulunmuyor. Ayrıca hoş bir şekilde bu el yazmasında sıfır sayısı da karşımıza çıkıyor.
Hint Rakamlarının Arap Dünyasına Yayılması

Sıfır sayısı 3. ve 4. yüzyıllarda, bir yer tutucu olarak Hint matematiğinde kullanılmaktaydı. Bilindiği üzere sıfırın sayı olarak kullanımını da Hintli bir matematikçi olan Brahmagupta‘ya (598–668) borçluyuz.
Arapların, Hint rakam sistemi ile bilinen ilk tanışmalarından biri M.S. 773 yılında Halife Mansur’a sunulan Hint astronomi kitapları ile olmuştur. İslamiyet’in yayılması ile birlikte artan Hint-Arap ilişkileri sonucunda da Hint rakamları Ortadoğu’da zaman içinde yaygınlaşmaya başlamıştır.
Bu esnada da akla gelen en önemli isim elbette M.S. 825 tarihlerinde Halife Memun’un izni ile, Hint matematiğini incelemek üzere Hindistan’a giden Harezmi gelmektedir. Harezmi, Abbasi Döneminin tanınmış matematik, coğrafya ve astronomi uzmanıdır.

Aynı zamanda cebirin babası olarak da tanıdığımız ünlü matematikçi Hindistan’daki matematik biliminden etkilenerek, Aryabhata’nın çalışmaları üzerine 820 yılında bir kitap yazmıştı. Bu kitabın Latince’ye çevrilmesiyle Hindistan’dan çıkan rakamlar Batı dünyasında hızlı bir yayılışa neden oldu.

Bunun için de İtalyan Leonardo Bigollo Pisano (1170 – 1250), ya da bildiğimiz adıyla Fibonacci’ye teşekkür etmeliyiz. Fibonacci, babasıyla yaptığı yolculuklar sonucunda tanıştığı Hint-Arap matematiğinden son derece etkilenmişti. Kendisi 13. yüzyılda Akdeniz dünyasını dolaştı ve zamanın en iyi Arap matematikçilerinden ders aldı. Bunun sonucunda 1202’de Liber Abaci adlı kitabı kaleme aldı. Kitap, Hint-Arap sembollerini Avrupa’ya tanıttı.
Avrupa’nın Yeni Rakamlara Adapte Olması Kolay Olmadı
Ancak ondalık aritmetiğin Avrupa’da tamamen yerleşmesi için birkaç yüzyıl daha geçmesi gerekiyordu. Romen rakamlarıyla hesaplama yapmak, ondalık sistemimize göre önemli ölçüde daha fazla zaman alır ve hataya açıktır. XXXI (31) ve XIV (14) Romen rakamlarını çarpmaya çalıştığınızı hayal edin. CDXXXIV (434) sonucunu elde etmek için ciddi bir çaba harcamanız gerekir. Ancak alışkanlıklardan vazgeçmek de kolay değildir.

Sonucunda zamanla Roma rakamlarının yerini bugünkü 0, 1, 2, 3, 4, 5, 6, 7, 8, ve 9 sembolleri aldı. Görüldüğü üzere günümüzde kullandığımız rakamların kökeni bir kaç açı ile açıklanamayacak kadar kapsamlıdır. Bu nedenle rakamlar ve açılar ile ilgili, tık tuzağı gibi de düşünmeniz gereken paylaşımlara itibar etmeyiniz.
Kaynaklar ve ileri okumalar:
- How Humans Invented Numbers—And How Numbers Reshaped Our World. Yayınlanma tarihi: 13 Mart 2017. Bağlantı: How Humans Invented Numbers—And How Numbers Reshaped Our World
- Magic numbers: the beauty of decimal notation. Yayınlanma tarihi: Kaynak site: Conversation. Bağlantı: Magic numbers: the beauty of decimal notation
- Why are the Arabic numerals shaped as they are?; Bağlantı: https://www.quora.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel