Sosyal medya uygulamalarından Netflix’e kadar algoritmalar tercihlerinizi öğrenir ve size gösterilen içeriğe öncelik verir. Google Haritalar ve yapay zeka, algoritmalar olmadan bir hiçtir. Bu cümleleri daha önceden duymuş olmanız olasıdır. Peki algoritma kelimesinin nereden geldiğini biliyor musunuz?

İnternet ve akıllı telefon uygulamalarından 1000 yıldan fazla bir süre önce, İranlı bilim insanı ve bilge, tam adı ile Ebu Abdullah Muhammed Bin Musa el Harezmi (780-850) – kısaca Harezmi- modern bilime şekil veren kişilerden biri olarak tarihe adını yazdırdı. Algoritma kelimesinin kökeni de onun adının Latince versiyonunda yer alan “algorithmi” kelimesinden gelmektedir.
Harezmi Kimdir?
El Harezmi, Abbasi Döneminin tanınmış matematik, coğrafya ve astronomi uzmanıdır. Onun sayesinde Avrupalı bilginler kullanılmakta oldukları Romen rakamları ile aritmetik yapmanın zorluğunu fark etmiştir. Harezmi onlara aritmetik hesaplamalar yapmanın daha kolay bir yolu olduğunu göstermiştir. Bu nedenle kendisi (Diophantus ile birlikte) “cebirin babası” bazılarına göre ” Bilgisayar biliminin büyükbabası ” olarak kabul edilir.

Harezmi’nin hayatı hakkında çok az ayrıntı bilinmektedir. Orijinal çalışmalarının çoğu zaman içinde kaybolmuştur. Ancak El-Harezmi’nin, günümüz Özbekistan’ında Aral Denizi’nin güneyindeki Harezm bölgesinde doğduğu kabul edilmektedir. Ayrıca “Bilimde Müslümanların Altın Çağı” olarak bilinen Abbasi Halifeliği döneminde yaşadığı da bilinmektedir.
Bu dönemde Halife el-Memun, Bağdat’ta Beyt-ül Hikmet adlı bir bilimsel akademi, bir rasathane ve bir kütüphaneden oluşan bir yer açmıştı. Bilinen adı ile “Bilgelik Evi” doktorların, hukukçuların, müzikçilerin, şairlerin ve bilim insanlarının bir arada toplandığı bir mekan halini almıştı.
Burada değerli kitaplar toplanıp Arapça ’ya çevrildi. Bu yer zamanla dönemin en zengin kütüphanesini, gözlem evini ve çoğunlukla matematik, astronomi ve yer bilimleri ağırlıklı, çeşitli çalışma birimlerini içine alan, çevrenin en yetkin bilim adamlarını toplayan, bir araştırma merkezi ve akademisi oldu. İslam matematikçilerinin Bilgelik Evi’nde üstlendiği en büyük projelerden biri cebiri geliştirmekti. Bu işin başında da Harezmi vardı.

Aryabhatta ve El Harezmi Elele: On Tabanlı Rakam Sistemi
Bir çok kişinin içine düştüğü yanılgı, 10 tabanlı rakam sistemini Harezmi’nin geliştirdiğidir. Oysa ki günümüzde kullandığımız rakamlar yani 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 simgelerini içeren rakam sistemi, Hint-Arap rakamları (Hindu-Arabic numerals / figures) olarak adlandırılmaktadır.
Bu rakamların dünya genelinde Hint – Arap rakamları olarak bilinmesinin nedeni de ilk olarak Hindistan’da şekillenmiş ve daha sonra Arap matematikçiler tarafından Batıya tanıtılmış olmasıdır. Bu rakamların kökeni ise Hintli matematikçi Aryabhata’nın ve çağdaşlarının çalışmalarına dayanıyor. 476-550 yılları arasında yaşayan Aryabhata Hint matematiğinin altın çağının ilk matematikçilerinden ve astronomlarındandır.

Hint rakam sistemi ile bilinen ilk tanışmalarından biri ise M.S. 773 yılında Halife Mansur’a sunulan Hint astronomi kitapları ile olmuştur. Harezmi ise Hindistan’daki matematik biliminden etkilenerek, Aryabhata’nın çalışmaları üzerine 820 yılında bir kitap yazmıştı. Bu kitabın Latince’ye çevrilmesiyle Hindistan’dan çıkan rakamlar Batı dünyasına hızla geçiş yaptı.
Cebiri Harezmi’mi Buldu?
Hayır. Cebiri Harezmi bulmadı. Onun yaşadığı dönemde cebri ve uygulamaları zaten biliniyordu. Ancak Harezmi bu konuda bir kitap yazan ilk kişiydi. MS 830 civarında, Halife el-Memun, Harezmi’yi “El Cebir V’el Mukabele” (Modelleyerek ya da Dönüştürerek Hesaplama) isimli kitabını yazmaya teşvik etti. Bu, onun en önemli eseri oldu. Eserinin pratik bir öğretim aracı olması amaçlanmıştı. Ancak Latince çevirisi, 16. yüzyıla kadar Avrupa üniversitelerindeki cebir ders kitaplarının temeliydi.

Kendisi kitabının birinci bölümde cebir kavramlarını, kurallarını ve şekillerin hacim – alan hesaplama yöntemlerini tanıttı. İkinci bölümde de miras davaları, arazi paylaşımı ve ticaret için hesaplamalar gibi gerçek yaşam problemlerine yer verdi ve çözümler üretti.
Harezmi kitabında sayılar ve semboller gibi modern matematiksel gösterimleri kullanmadı. Bunun yerine, basit bir düzyazıyla yazdı ve geometrik diyagramlar kullandı. Onun düşünce mantığını kavramak için bir örnek üzerinden gidelim.
Harezmi’nin Denklem Çözme Mantığı
Denklemimiz x2+10x=39 olsun. Bu denklem Harezmi tarafından bu denklemi “Hangi sayının karesi, sayının 10 katı ile toplanırsa 39 eder?” biçiminde ifade edilmekteydi.
Burada x2 terimi kenar uzunluğu x olan bir kareyi temsil eder. Denklemdeki +10x terimi ise kenar uzunluğunun 10 katının, karenin alanına eklendiğini gösterir. Denklemin sağındaki 39 sayısı, karenin alanına kenarın 10 katı eklendikten sonraki toplam alanın değeridir. Diğer bir deyişle, x2 +10x teriminin temsil ettiği yeni alan 39’a eşittir.
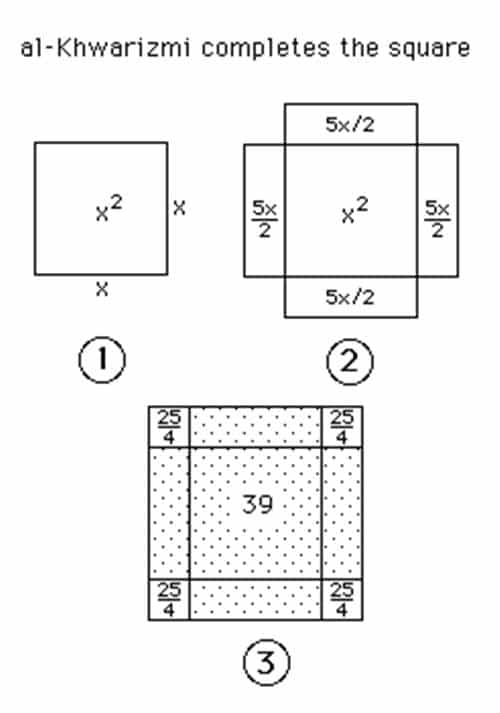
Harezmi, alanı 39 olan şekli, kareye tamamlamak ister. Böylece yeni (hayali) karenin kenar uzunluğunu hesaplayabilecektir. 10x terimi ile gösterilen dikdörtgenin alanı 4 eşit parçaya bölüp, kenar uzunluğu x olan orijinal karenin dört tarafına ekler. Bu dikdörtgenlerin bir kenarı x uzunlukta olacağı için, diğer kenar doğal olarak 10/4 veya 5/2 olur.
Yeni şeklin toplam alanı 39’a eşittir. Ancak yeni şekil henüz kare değildir, çünkü köşelerde dört küçük boşluk vardır. Köşelerdeki boşluklar, kenar uzunluğu 5/2 olan karelerdir. Bu nedenle her küçük karenin alanı, 5/2’nin karesine eşittir veya 25/4’tür. Dört küçük karenin toplam alanını bulmak için 25/4’ü 4’le çarpınca 25 çıkar.
Bir önceki yeni şeklin alanı 39 idi, bu alana 25 eklenince 64 çıkar ve karenin bir kenarını 8 bulur. Sonrasında 8 sayısından iki küçük karenin kenar uzunluğunu çıkartarak, x değerini bulur. Küçük karelerin kenar uzunlukları 5/2 idi. İki küçük karenin kenarlarının toplamı, 2 çarpı 5/2 yani 5’tir. Büyük karenin kenar uzunluğu olan 8’den 5 çıkarılınca x değeri 3 olarak bulunacaktır.
Algoritma ile Harezmî’nin İlgisi Nedir?
El-Harezmi’nin matematiksel problemleri hesaplama biçimi, modern algoritma kavramının temelini oluşturmuştur. Ayrıca kendisi kitabında, dört temel işlemi (toplama, çıkarma, çarpma, bölme) gerçekleştirmek ve kesirleri hesaplamak için ondalık gösterimi kullanmaya ilişkin ilk ayrıntılı açıklamaları yapmıştır.

El-Harezmi, matematik ve bilgisayar biliminin bugün bildiğimiz şekliyle gelişmesinde merkezi bir rol oynamıştır. Bir dahaki sefere sosyal medya akışınızdan çevrimiçi banka hesabınıza ve Spotify uygulamanıza kadar herhangi bir dijital teknolojiyi kullandığınızda, bunların hiçbirinin onun öncü çalışmaları olmadan mümkün olmayacağını unutmayın.
Kaynaklar ve ileri okumalar:
- Why algorithms are called algorithms. Yayınlanma tarihi: 9 Temmuz 2022. Kaynak site: BBC. Bağlantı: Why algorithms are called algorithms./
- Why are algorithms called algorithms? A brief history of the Persian polymath you’ve likely never heard of. Yayınlanma tarihi: 8 Mayıs 2024. Kaynak site: Conversation. Bağlantı: Why are algorithms called algorithms? A brief history of the Persian polymath you’ve likely never heard of
- Renima, A., Tiliouine, H., Estes, R.J. (2016). The Islamic Golden Age: A Story of the Triumph of the Islamic Civilization. In: Tiliouine, H., Estes, R. (eds) The State of Social Progress of Islamic Societies. International Handbooks of Quality-of-Life. Springer, Cham. https://doi.org/10.1007/978-3-319-24774-8_2
Matematiksel



