MS 628’de, Rajasthan’daki bir dağda yaşayan bir Hintli bilge, dünyanın en önemli matematiksel keşiflerinden birini yaptı. Büyük matematikçi Brahmagupta (598-670), hiçlik ve boşluk hakkındaki Hint felsefi fikirlerini araştırdı ve sıfır kavramını tanımlayan bir inceleme ortaya koydu.
Biz ona sıfır desek de dünya onu sūnya, nulla, ṣifr, zevero, zip ve zilch gibi isimlerle tanımladı. Bunların hepsi olmayan bir şeyi bir hiçliği tanımlamaya çalıştı. Tarihçiler ve diğerleri bu sayının doğum yeri için birbirinden farklı yerlere işaret etti. Sıfır sayısının tarihini anlamak çok da kolay olmadı.
Sıfır sayısı bir şeyin yokluğu anlamına gelir ve aslına bakarsanız bir şeyin yokluğunu kavramak zor kavramdır. Brahmagupta’nın ona bir anlam katmasından önce başka uygarlıklar da sıfır sayısını kullanmıştı. Ancak tüm gösterimlerde sıfır bir sayı olarak değil, yer tutucu görevi görüyordu. Aşağıdaki görselde bilinen ilk sıfır sayısını görüyorsunuz.
Gördüğünüz nokta sembolü daha sonrasında günümüz sıfır sayısına evrilecekti. Noktanın sayı statüsünü kazanması is Hintli gökbilimci ve matematikçi Brahmagupta sayesinde mümkün olacaktı.
Brahmagupta Kimdir?
Brahmagupta, Hint matematikçi ve astronomdur. Yaklaşık olarak MS 598 – 668 yılları arasında yaşadığı düşünülmektedir. Hindistan’da Aryabhata’dan sonraki en etkili matematikçilerden biri olarak kabul edilir.
Hayatı hakkında pek bir şey bilinmese de onun matematik, astronomi ve bilime yaptığı katkılar modern dünyayı şekillendirmiştir. Bunun nedeni de sıfır sayısının özelliklerini keşfeden ve fikirlerini yazılı olarak kaydeden ilk matematikçi olmasıdır.
“Herhangi bir sayıdan kendisinin çıkarılması sıfırdır. Bir sayının sıfır ile çarpılması sonucu sıfır yapar. Herhangi bir sayının sıfır ile toplanması ya da çıkarılması sayının kendisini verir. ” gibi günümüzde sıfır sayısı ile ilgili aşina olduğumuz tanımlamaları ilk ortaya koyan kişi kendisidir.
Brahmagupta aynı zamanda pozitif ve negatif sayıların sıfır ile olan aritmetik kurallarını ortaya koyan ilk kişidir. Ancak bunu servetler ve borçlar adı altında yapacaktı. Kendisi pozitif sayıları “servet”, negatif sayıları “borç” olarak adlandırır.
Sonrasında da bunu “Borç eksi sıfır borçtur. Bir servet eksi sıfır bir servettir. Sıfırdan çıkartılan borç bir servettir. Sıfırdan çıkarılan bir servet borçtur.” gibi cümlelerle tanımlamıştır. Sonucunda tanımlamalar bakıldığında kavram olarak karşımıza pozitif ve negatif sayılar çıkar.
Aslına bakarsanız ikinci dereceden denklem çözümünün formülünü bulan ilk kişidir. İlk n doğal sayının karelerinin toplamını n(n + 1)(2n + 1) / 6 olarak ve ilk n doğal sayının küplerinin toplamını (n(n + 1) / 2 olarak verir. Fakat bu özellikleri nasıl bulduğuna dair kanıtları yayınlamadığından işlem yollarına nasıl eriştiği günümüzde mevcut değildir.
Ayrıca Pi’nin yani bir çemberin çevresinin çapına oranının genellikle 3 olabileceğini ve bunun için 10’nun karekökünün kullanılması gerektiğini söyler ki bu değer 3,162’ye eşittir. Yani Pi’nin gerçek değerini yüzde 0,66 daha yüksek bulur. Elbette bu çalışmaları yaparken Brahmagupta yalnız değildi. Aslında kendisi daha önceki bir Hint dehası olan Aryabhata’nın (476–550) omuzlarında duruyordu.
“Brahmagupta Teoremi” Nedir?
Bu iki adamın fikirleri, antik Hindistan’ın matematiksel öğrenimini bir araya getirerek önce Arap dünyasına, sonra da uzak batıya doğru seyahat etti ve bize yalnızca sıfır gibi önemli matematiksel kavramları değil, aynı zamanda bugün kullandığımız sayıların biçimini de verdi.
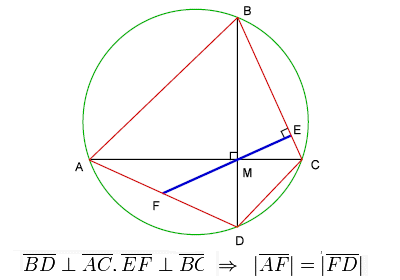
Brahmagupta aynı zamanda, köşeleri bir dairenin içine değen dört taraflı bir şeklin alanını göstermek için de bir formül bulur. Aslında günümüzde bir üçgenin alanını hesaplamak için kullandığımız Heron formülü, onun bulduğu formülün özelleştirilmiş halidir.
Öklid geometrisinde, Brahmagupta formülü, kenarların uzunlukları göz önüne alındığında herhangi bir kirişler dörtgeninin (daire içine çizilebilen dörtgen) alanını bulmak için kullanılır. ( Detaylara buradan erişebilirsiniz.)
Brahmagupta öncelikle bir gökbilimciydi, ancak bu alandaki çalışmalarının çoğu matematiğe yayılacaktı. Mesela Dünya’nın Ay’a Güneş’ten daha yakın olduğunu keşfetti. Brahmagupta bunu Güneş’in yarattığı ışık ve gölgelerin açılarını ve Ay’ın görünümünü yorumlayarak hesapladı. Ayrıca bir yılın tam uzunluğunu ve Dünya’nın çevresini şaşırtıcı bir doğrulukla hesapladı.
Ancak Brahmagupta’nın en uzun süreli keşifleri cebir, sayılar teorisi ve geometri alanındaydı. Genel doğrusal denklemin ve genel ikinci dereceden denklemin çözümü de dahil olmak üzere birçok çığır açan cebirsel fikir ortaya koydu. Brahmagupta aynı zamanda kesirleri bugün düşündüğümüz görsel forma sokan ilk matematikçiydi. Kitabında kesirlerin nasıl toplandığını, çıkarıldığını, çarpıldığını ve bölündüğünü açıklar.
Sonuç olarak;
Brahmagupta’nın çalışmaları, Hint matematiğinin ve astronomisinin gelişimine büyük katkılarda bulundu. Onun eserleri önce Arap dünyasına ve sonrasında da ve Orta Çağ’da Avrupa matematiğine önemli katkılarda bulundu.
Kaynaklar ve ileri okumalar:
- ‘In Britain, we are still astonishingly ignorant. The hidden story of how ancient India shaped the west. Yayınlanma tarihi: 1 Temmuz 2024. Kaynak site: Guardian. Bağlantı: ‘In Britain, we are still astonishingly ignorant. The hidden story of how ancient India shaped the west
- “Brahmagupta” (Erişim Tarihi: 17.11.2019); http://mathshistory.st-andrews.ac.uk/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel
