Günlük yaşamda, tamamen mantıksız olmadığımız zamanlarda, genellikle iki tür akıl yürütme kullanırız. Bunlardan biri tümevarımdır. Bu akıl yürütme yöntemi sayesinde de çevremizde gördüklerimizden genel bir sonuç çıkarmaya çalışırız.

Örneğin şu ana kadar her zaman beyaz kürklü koyunlar ile karşılaştıysanız, tümevarım yöntemi ile genelleme yapıp tüm koyunların beyaz olduğunu söyleyebilirsiniz. Bu akıl yürütme biçimi elbette dönem dönem faydalıdır ve bilimde bu nedenle de sık kullanılır.
Ancak bazı sakıncaları da vardır. Evrendeki her koyunu gördüğünüzden asla emin olamazsınız. Belki de bir yerlerde henüz karşınıza çıkmamış siyah bir koyun vardır. Bu yöntemle vardığınız sonucun gerçekten doğru olduğundan emin olamazsınız. Bu yüzden tümevarım ile elde ettiğiniz sonuçları her zaman gözden geçirmeye açık olmalısınız.

Tümdengelim ise ikinci akıl yürütme biçimidir ve aslında tümevarımın tam tersidir. Doğru olduğundan emin olduğunuz genel bir ifadeden yola çıkarsınız. Sonrasında da belirli bir durum hakkında sonuçlar çıkarırsınız. Örneğin, bütün koyunların ot yemeyi sevdiğini biliyorsanız ve karşınızda duran canlının da bir koyun olduğunu biliyorsanız, o zaman onun otu sevdiğini de kesin olarak bilirsiniz.
Bu akıl yürütme biçimi elbette faydalıdır ancak onun da bir sınırlaması vardır. Eğer ilk önermeniz yanlışsa, yani tüm koyunların otu sevmesi konusunda yanılıyorsanız veya gözleminiz yanlışsa, yani baktığınız yaratık aslında bir koyun değilse ulaştığınız sonuç da hatalı olacaktır.
Matematikçiler Neden Sürekli Bir Şeyleri İspat Etmek İsterler?
Matematik belki de mutlak kesinliğin mümkün olduğu tek alandır. Bu yüzden matematikçiler ispatlara çok değer verirler. Ayrıca, ispatlarda ısrar etmezsek, işin içine fark edilemeyen küçük hatalar sızar. Bunun bir örneğini Öklid’den verebiliriz.
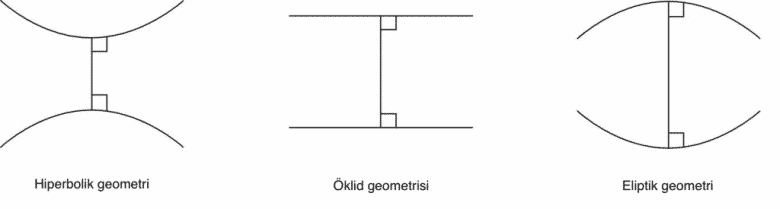
Öklid’in aksiyomlarından biri, tüm üçgenlerin iç açılarının toplamının 180 derece olduğunu söylemeye eşdeğerdir. Bu Öklid’in Beşinci Ppostulatı olarak bilinmektedir. Yüzyıllar boyunca matematikçiler beşinci postülanın ilk dördünün doğrudan bir sonucu olduğunu kanıtlamaya çalıştı ancak tüm girişimler başarısız oldu. Yine de Öklid geometrisi egemenliğini sürdürdü.
Derken 1800’lerin başında matematikçiler iki yeni geometri keşfetti. Bu büyük değişiklikte dört
matematikçi kilit rol oynadı: Gauss, Riemann, Nikolay Lobaçevski ve Janos Bolyai.
Küskün Bir Matematikçi: Janos Bolyai
Janos Bolyai, hayatının çoğunu günümüz Romanya’sının Transilvanya dağlarının vahşi doğasında, Almanya, Fransa ve İngiltere’nin ana akım matematik topluluklarından uzakta geçiren bir Macar matematikçiydi. Babası ve öğretmeni Farkas Bolyai bir süre Gauss’un öğrencisi olmuş başarılı bir matematikçiydi. Janos Bolyai de yetenekli bir çocuktu. Matematiğin yanı sıra keman çalıyor ve eskrim dersleri alıyordu.

13 yaşına geldiğinde matematikte bir çok konuda ustalaşmıştı. Lise eğitiminin ardından, Viyana Askeri Okuluna kaydoldu. 1823’de teğmen olarak mezun oldu. Bu esnada bir hobi olarak matematik çalışmaya devam ediyordu. O sırada babasının takıntısı olan Öklid’in Beşinci Postulatı ile tanıştı.
Gauss’un yanında eğitim görmüş olan Farkas, beşinci postulatın diğer dördünden türetilebileceğine dair bir kanıt bulduğuna iki kez inanmıştı. Ancak kanıt her iki sefer Gauss tarafından çürütülmüştü. Teoremi kanıtlamaya çalışırken nasıl yorgun düştüğünü çok iyi bildiğinden, Farkas oğlunu bu çalışmanın sağlığını, iç huzurunu ve mutluluğunu elinden alacağı konusunda uyarmıştı.
Farkas ona yazdığı bir mektupta “Ben tüm hayat ışığımı ve zevkimi söndüren bu dipsiz geceden geçtim. Sana yalvarıyorum, paralellik biliminden uzak dur!” diyerek oğlunu uyarsa da Janos babasının uyarılarını dikkate almadı.
Hiperbolik Geometrinin Keşfi ile Yeni Geometrilerin Anlaşılması
Bolyai öncelikle bilimde sık kullanılan bir strateji olan reductio ad absürdüm ile beşinci postulatı kanıtlamaya girişti. Bu yaklaşımda, araştırmacı bir postulatın yanlış olduğunu varsayar. Sonra, böyle bir varsayımın çelişkili sonuçlara yol açtığını gösterir. Böylece o postulatın aslında doğru olması gerektiğini ortaya koyar.
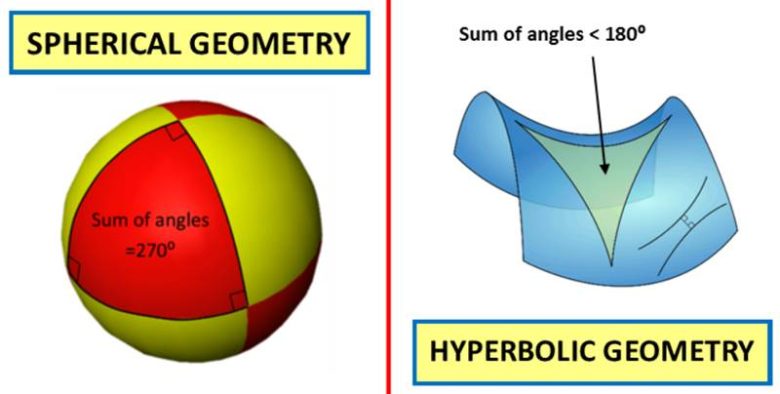
Ama bunu ortaya koymak yerine, Bolyai 1820’lerde “hayali bir geometri” buldu. Eyer biçimli görünümü nedeniyle “hiperbolik” olarak adlandırılan bu geometride, üçgenin iç açılarının toplamı 180 dereceden daha azdı ve bir doğruya paralel olan sonsuz sayıda doğru vardı.
1823’te babasına yazdığı mektupta “Beni hayretler içinde bırakacak kadar harika şeyler keşfettim. Hiçlikten garip yeni bir dünya yarattım” diyen Bolyai çalışmasını 1831’de, babasının yazdığı daha kapsamlı bir eserin parçası olarak yayımladı.
Çalışmayı okuyan Gauss’un dikkatini en çok Janos’un yazdığı bölüm çekmişti. Gauss bunun üzerine Farkas’a yazdığı mektupta eski dostunun oğluyla gurur duyması gerektiğini ancak Janos’un fikirlerinin tamamını kendisinin zaten bulduğunu, sadece henüz yazıya dökmediğini söyledi. Gauss’un bu cevabı Janos’un matematik kariyerini daha başlamadan bitirmişti.

Janos’un hayatındaki kırılma noktalarından biri de 1848’de Lobachevsky’nin yazdıklarına ulaşması oldu. Rus şehri Kazan’da, matematikçi Nikolai İvanoviç Lobaçevski aynı tür “hayali geometri”yi yani hiperbolik geometriyi bulmuştu. Bulgularıyla ilgili makalesi 1829-30 tarihlerinde Kazan Habercisi’nde (Kazan Üniversitesi’nin Rusça basılan bir yayını) yayımlanmış ama pek okuyan olmamıştı.
Sonuç olarak
Kendi fikirlerinin bir başkası tarafından da yayımlanmış olduğunu görünce var olan ruhsal sorunları iyice açığa çıktı. Devamında János Bolyai dünyaya küstü ve uzun süreliğine inzivaya çekildi. Bir daha matematik ile asla uğraşmadı.
Uzun süren hastalıklarının ardından 1860 yılında hayata veda etti. Mezar taşına “Ünlü matematikçiler arasında da en ünlüsüydü, ama ne yazık ki, büyük yeteneği kullanılamadan heba oldu” diye yazılacaktı. Janos Bolyai adı bugün Ay’da onun adı verilen bir kraterde yaşıyor. Ancak o bundan habersiz küskün bir biçimde bu dünyadan ayrıldı.
Kaynaklar ve ileri okumalar:
- Marianne Freiberger; Why we want proof. Yayınlanma tarihi: 10 Nisan 2015; Bağlantı: Marianne Freiberger; Why we want proof
- Farkas Bolyai; Bağlantı: https://tr.wikipedia.org
- János Bolyai; Bağlantı: https://tr.wikipedia.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel