2000 yılı aşkın bir süre önce Yunan matematikçi Öklid, geometrinin üzerine inşa edilmesi gerektiğini düşündüğü beş maddeden oluşan bir liste ortaya attı. Öklid’in ilk dört varsayımı basit, tartışmasız ve sezgiselken, beşincisi apaçık olmaktan uzak idi. Yüzyıllar boyunca onlarca matematikçi ilk dört aksiyomu kullanarak beşincisini kanıtlamaya çalıştı ama olmadı. Bu arayış aslında yeni geometrilerin bulunmasına neden olacaktı. Bu yeni geometrilerden birisi de Hiperbolik Geometri idi.
Carl Friedrich Gauss (1777-1855), Janos Bolyai (1802-1860), Nikolai İvanoviç Lobaçevski (1793-1856) gibi matematikçiler sonucunda Öklid dışı geometrilerin doğmasına önayak oldular. Öklid dışı geometrilerin keşfi, sadece matematik değil düşünce tarihinde de bir dönüm noktası olarak kabul edilmektedir.
1829’da Rus matematikçi Nicolai Lobachevsky, On the Principles of Geometry (Geometrinin İlkeleri) adlı kitabını yayınladı. Kendisi paralellik varsayımını yanlışlayan bir geometri hayal etti. Ancak aslında bu esnada bir başka matematikçi de aynı sonuçlara varmıştı.
Matematikçi János Bolyai ile Nikolay Lobaçevski’nin birbirinden bağımsız keşfettiği şey beşinci postulatı gerektirmeyen, daha farklı bir geometrinin var olabileceği idi. Günümüzde onların bu keşiflerini hiperbolik geometri ya da Lobaçevski geometrisi dite biliyoruz.
Özgünlüklerinden ötürü saygı duyulması gereken fikirler, dönemin gelen algısına uygun olmaz ise çoğunlukla saçma olarak tanımlanır. Lobaçevski için de aynı süreç geçerliydi. Sonuçta Öklid geometrisi bir geleneğe dayanıyordu ve gelenekleri bir anda yıkmak hiçbir zaman kolay olmamıştı. Çalışmasını bir çok üniversite kayda değer bulmadı. Dönemin matematikçileri tarafından tepki ile karşılandı. Geometriya nihayet 1909’da ölümünden çok sonra orijinal haliyle yayınlandı.

Kısaca Nikolay Lobaçevski
Polonyalı göçmen bir ailenin oğlu olarak dünyaya gelen Nikolai babasının erken ölümü üzerine annesi ile birlikte neredeyse tüm yaşamını Batı Sibirya’daki Kazan’da geçirdi.1807’de Tıp okumak için Kazan Üniversitesi’ne gitti ama kısa süre sonra matematik ve fiziğe ilgi duymaya başladı. 1811’de matematik ve fizik alanında yüksek lisans derecesi kazandı ve kariyerine 1822’de profesör olarak devam etti.

1827’de üniversitede rektör oldu ve bu sıralarda Kazan Üniversitesi en parlak dönemlerini yaşadı. 1832’de 40 yaşında iken kendinden çok daha genç ve zengin bir kadın olan Leydi Varvara Moisieva ile evlendiler. 7 çocuğu, lüks bir evi ve keyifli bir sosyal yaşamları oldu. Ancak bu yaşam nihayetinde emekliliği için ona çok az para bıraktı. Sağlığı kötüleşti ve 1846’da üniversite onu zorunlu bir biçimde emekli etti. Zamanla görme yetisini yitirdi ve 1856’da yoksulluk içinde öldü,
Hiperbolik Geometri Nedir?
Yazının bundan sonrasının anlaşılması adına tekrardan Öklid geometrisine geri dönmeniz gerekiyor. Öklid geometrisinde hepimizin bildiği ilk kurallardan birisin bir üçgende iç açılar toplamının 180 derece olduğudur. Ancak aslında bu bilgi her zaman doğru değildir.
Örneğin küresel geometri de, yani bir küre üzerindeki geometride büyük ölçekte düşündüğümüz zamanlarda bir üçgenin iç açıları toplamı 180 dereceden çok daha fazladır. Bunun neye benzediğini aşağıdaki dünya örneğinden görebilirsiniz.
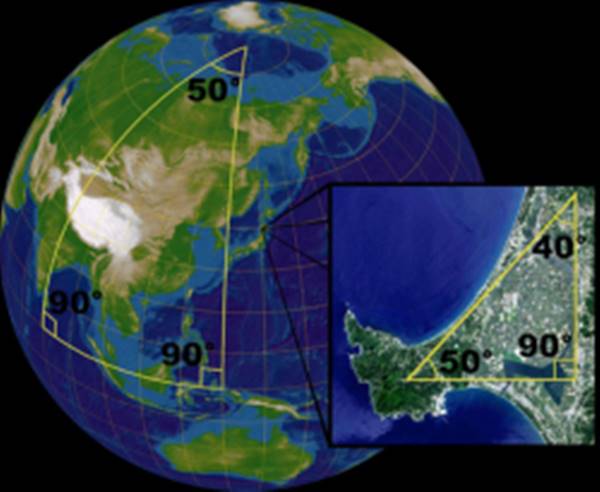
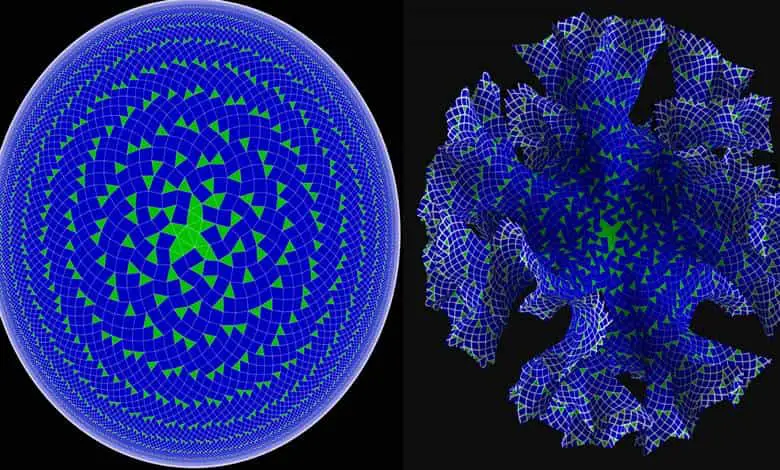
Küre, matematikçilerin pozitif eğrilik dediği şeye sahiptir ve bu sezgisel olarak mantıklıdır. Ancak işleri diğer yöne götüren başka bir geometri daha var. Hiperbolik geometrinin görselleştirilmesi küresel geometri kadar kolay değildir. Çünkü üç boyutlu Öklid uzayında bozulma olmadan modellenemez.
Detaylara geçmeden önce bir hiperbolik düzlemde yaşamanın nasıl olacağını anlamaya çalışalım. Diyelim ki, aşağıdaki şekilde mavi daire ile sınırlanan bölgenin içinde yaşayan bir karınca olsun. Öklid geometrisinde bu şeklin içindeki iki nokta arasındaki en kısa yol düz bir çizgi olmalıdır. Ancak hiperbolik geometride mesafeler farklı şekilde ölçülür. Bu nedenle en kısa yol artık bir Öklid düz çizgisi boyunca değil, şekilde kırmızı ile gösterilen gibi, diskin sınırını dik açılarla karşılayan bir dairenin yayı boyuncadır.
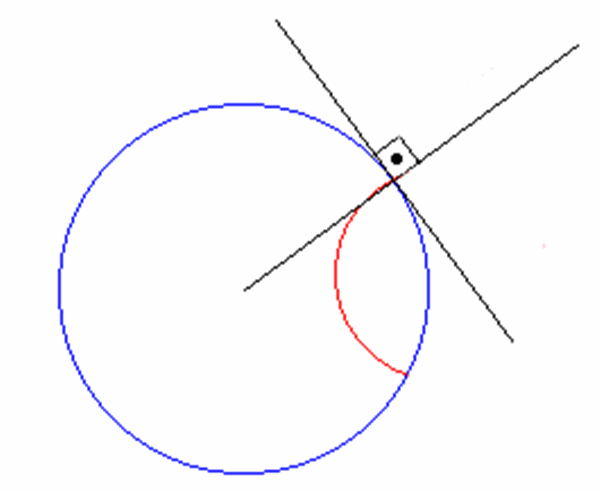
Kenarları yarım dairelerin yayları olan hiperbolik bir üçgenin açıları toplamı 180 dereceden az olan açılara sahiptir. Aşağıdaki şekildeki tüm siyah beyaz şekiller hiperbolik üçgenlerdir.

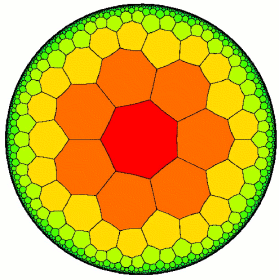
Hiperbolik ölçünün bir sonucu, diskin sınır dairesinin içinde duran karıncanın bakış açısından sonsuz derecede uzakta olmasıdır. Öklid geometrisinin aksine, hiperbolik geometride yollar dışa yaklaştıkça daha uzun olur. Örneğin aşağıdaki şekil düzgün yedigenler ile döşenmiştir. Bu durumda merkezde duran bir karıncanın bu şeklin dışına çıkmak için geçmesi gereken çok sayıda çokgen vardır. Pozitif eğriliği olan kürenin aksine, hiperbolik düzlem negatif eğimlidir.
Hiperbolik Geometri İlginç Bir Geometridir
Hiperbolik geometri, muhtemelen size hayali bir matematiksel yapı gibi gelmiştir. Bu nedenle gerçek hayatta işe yaramaz da diyebilirsiniz. Einstein 1905’te özel görelilik teorisini geliştirdiğinde, hiperbolik geometri simetrilerinin, teorisini formüle etmek için tam olarak ihtiyaç duyduğu şey olduğuna karar vermişti. Günümüzde matematikçiler hiperbolik geometrinin Facebook gibi büyük ağ yapılarını anlamaya yardımcı olacağını düşünüyor. Sonuç olarak Öklid dışı geometriler, insanın geometriyi doğru bir biçimde anlama, fiziksel uzayın gerçek niteliğini keşfetme girişimleri açısından hayati önemdedir.
Kaynaklar ve ileri okumalar:
- Maths in a minute: Not always 180; Yayınlanma tarihi: 3 Temmuz 2013; Bağlantı: https://plus.maths.org/
- Ian Stewart; Significant Figures: The Lives and Work of Great Mathematicians; ISBNs: 978-0-465-09612-1
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










